6.4.1 锁相环基础
锁相环(PLL)一般是由鉴相器(PD)、环路滤波器(LF)和压控振荡器(VCO)组成的,其数学模型如图6.10所示。
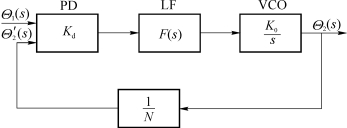
图6.10 PLL的数学模型
通过PLL的数学模型,得到传递函数H(s)为
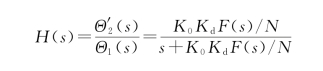
误差传递函数
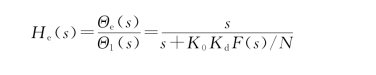
式中:ω0为VCO的中心角频率;K 0为VCO增益;K d为鉴别器增益。
对于锁定的环路,当输入的频率和相位在线性范围内发生某种变化时,环路将使振荡器的频率和相位跟踪输入信号的变化。假如输入信号的频率和相位变化是有规律的,那么在输入变化时,环路将有一瞬态响应过程,在瞬态响应过程结束之后,环路会存在一个稳态跟踪相差(也可能为零)。这个稳态跟踪相差是时间趋于无穷大、系统进入稳定状态后的静态误差,通常用θe(∝)表示,直接使用拉普拉斯变换终值定理即可求得,其表达式为
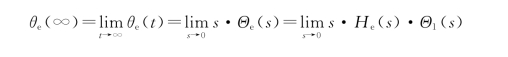
1.输入频率阶跃(相位斜升)
输入信号产生频率阶跃的原因很多,例如,收发信号之间有一实际频差或者有一多普勒频移等。这时输入相位为相位斜升θ1(t)=Δω·t,其中Δω为频率阶跃量,如图6.11所示。
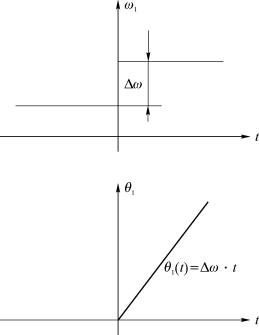
图6.11 输入频率阶跃信号
其拉普拉斯变换式为
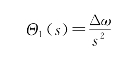
其稳态相差为
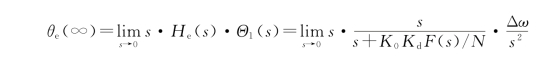
对于采用无源比例积分滤波器的二阶环,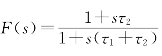
,其跟踪频率阶跃信号时存在稳态跟踪误差
;对于采用理想比例积分滤波器的三阶环,F(s)=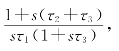
其跟踪频率阶跃信号时稳态跟踪误差为0。
2.输入频率斜升
收、发信机之间的加速运动会使输入信号频率以速率R(rad/s2)随时间作线性变化,输入相位则以加速度随时间变化
,如图6.12所示。
其拉普拉斯变换式为
其稳态相差为
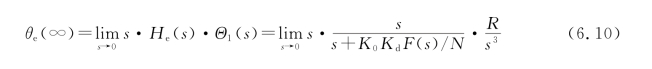
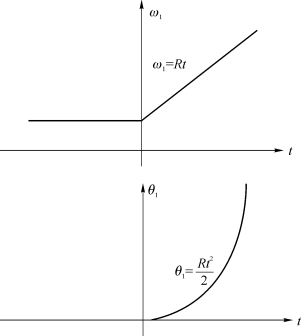
图6.12 输入频率斜升信号
对于采用无源比例积分滤波器的二阶环,F(s)=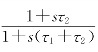
,其跟踪频率斜升信号时稳态跟踪误差θe(∞)→∞,即趋于无穷大;对于采用理想比例积分滤波器的三阶环,F(s)=
,其跟踪频率斜升信号时稳态跟踪误差为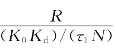
;如果采用二级理想比例积分滤波器构成三阶环路,则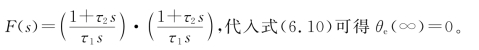
由以上分析可知,对于同一种锁相环路来说,输入信号变化得越快,跟踪性能就越差。而同一信号加入不同的锁相环路,其稳态相差是不同的。对于频率阶跃信号,采用无源比例积分滤波器的二阶环将有固定的稳态相差,而三阶环则能无误差地跟踪。对于频率斜升信号,二阶环已无法跟踪,三阶环跟踪时有固定的稳态相差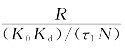
,理想三阶环更可以做到无误差跟踪。在旋转接收机中,既要跟踪相位阶跃,又要跟踪频率阶跃和频率斜升,所以可以采用三阶环,这样会提高系统精度。
频率估计可通过传统的锁相环得到,低阶锁相环环路动态性能和抗干扰性能对环路带宽的不同要求,使得它不适合旋转环境的要求。而采用高阶锁相环,例如三阶环可大大减小由频率阶跃和频率斜升引起的相位误差,具有比低阶环好得多的多普勒频移跟踪性能。高阶环可在动态性能和抗干扰性能两方面求得平衡,从而适应旋转环境对多普勒频率跟踪的需要。