6.4.2 高阶锁相环
为提高频率跟踪效果,应采用高阶锁相环,但高阶锁相环的设计较复杂。本书分别设计了三阶锁相环路和四阶锁相环路,通过仿真实验,拟采用高阶(四阶)锁相环路作为跟踪环路。下面介绍三阶PLL和四阶PLL的设计。
1.三阶PLL设计
为了得到三阶PLL,必须使用二阶环路滤波器。当然,这样的滤波器可以采用无源超前-滞后、有源超前-滞后或者有源比例积分滤波器。所有这些滤波器都会有两个极点。一般实践中构建的二阶环路滤波器具有共轭复数极点对。电阻、电容实现的无源超前-滞后滤波器不能实现复数极点,而是所有的极点位于s平面的负实轴上。为了使这类滤波器具有复数极点,必须使用电感器。大多数设计者设计滤波器时都回避使用电感,而使用有源RC滤波器,出于这样的原因,我们撇开无源超前-滞后滤波器,使用有源滤波器。
二阶有源超前-滞后环路滤波器的传输函数F(s)形式如下:
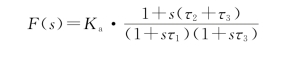
其中,τ1=R 1C 1,τ2=R 2C 2,K a=C 1/C 2。更一般的F(s)表达式为
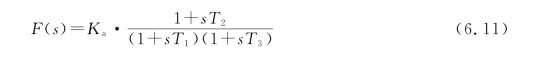
不难看出,T 1=τ1,T 2=τ2+τ3,T 3=τ3。
设计二阶环路滤波器,关键是安排极点和零点的位置,设计步骤如下:
①确定ω3d B带宽。
通常设计者知道PLL需要的带宽,因此从选择ω3dB开始比较合理。缺省值可以取:ω3d B=
,其中
是PLL的中心频率(弧度)。本设计选取:f 0=200 Hz,所以
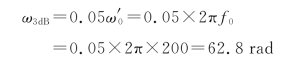
②计算截止频率ωT。
通过稳定度分析,选取ωT=ω3dB/1.33,所以
③选择转折点频率ω2、ω3。
为了获得足够的相位裕度,建议:
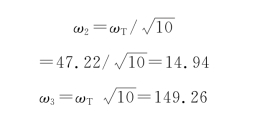
④选择转折点频率ω1和K a。
建议设置:
ω1=ω2/10=14.94/10=1.49
这样,在整个的十倍频中开环增益以-40 d B/dec滚降。选择K a,使得ωT时开环增益恰好是1,其表达式为
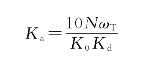
取N=1,K 0=10,K d=1/2,则
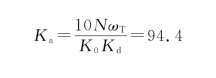
⑤计算时间常数T。
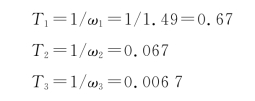
代入式(6.11),得
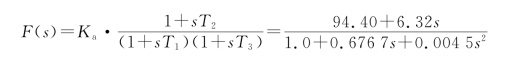
2.四阶PLL设计
为了得到四阶PLL,必须使用三阶环路滤波器。当然,这样的滤波器可以采用无源超前-滞后、有源超前-滞后或者有源比例积分滤波器。所有这些滤波器都会有3个极点。一般实践中构建的三阶滤波器具有共轭复数极点对。这里只讨论有源滤波器。
可以利用许多方法实现三阶环路滤波器。一个三阶超前-滞后环路滤波器的实现方案如图6.13所示。
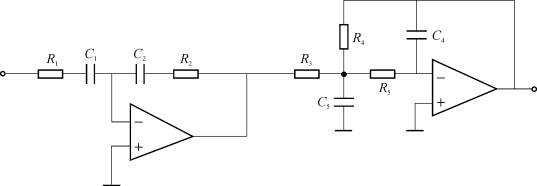
图6.13 三阶超前-滞后环路滤波器的实现
图中滤波器由两部分组成。第一部分是一阶超前-滞后滤波器;第二部分是二阶低通滤波器。可以利用两个实极点或共轭复数极点对实现。当第二个滤波器的极点是实数时,可把滤波器的传输函数F(s)写成如下形式:
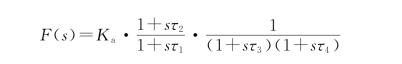
其中,τ1=R 1C 1,τ2=R 2C 2,K a=C 1/C 2。当滤波器第二部分形成复数极点对时,实际中一般采用不同的表达式表示F(s):
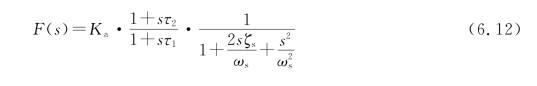
在第二种情况中,ωs是自然频率,ξs是二阶频率响应的阻尼因子。四阶PLL的开环传输函数G(s)可以有两种表达方式,其一用于实数极点,其二用于复数极点。对于实数极点,G(s)写成
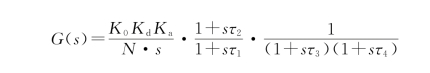
式中:K 0为VCO增益;K d为鉴相器增益。
对于复数极点,G(s)为
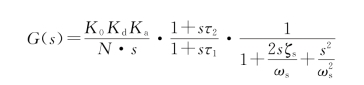
幅度曲线如图6.14所示。第一个滤波器部分具有一个极点s=-ω1和一个零点s=-ω2,所以幅度渐近线在ω1、ω2提供了转折点。假设第二个滤波器部分的极点是实数,位于s=-ω3和s=-ω4,那么该滤波器部分在ω3和ω4产生了两个转折点。在ω3和ω4,幅度曲线的斜率增加-20 dB/dec;然而,当第二个滤波器部分的极点是复数时,仅在ωs有一个附加转折点,在这个点,斜率增加-40 d B/dec。
设计三阶环路滤波器的步骤如下。
①确定ω3dB带宽。
与设计二阶环路滤波器相同,从选择ω3dB开始。缺省值可以取:ω3dB=0.05ω′0,其中ω′0是PLL的中心频率(单位是弧度)。本设计选取:f 0=200 Hz,所以
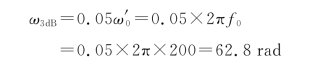
②计算截止频率ωT。
与二阶滤波器设计类似,选取:
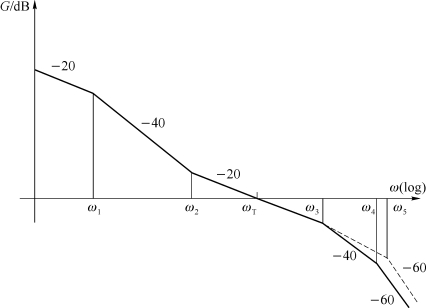
图6.14 幅度曲线(虚线为复数极点)
③选择转折点频率ω2。
为了获得足够的相位裕度,建议:
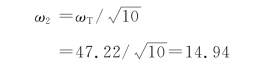
④选择转折点频率ω1、K a。
建议设置:
这样,在整个的十倍频中开环增益以-40 d B/dec滚降。选择K a,使得ωT时开环增益恰好是1,其表达式为
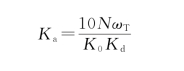
取N=1,K 0=10,K d=2/π,则
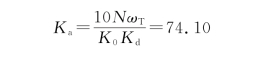
⑤计算时间常数τ1,τ2。
利用τ1=1/ω1,τ2=1/ω2确定。
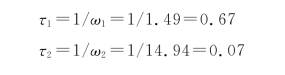
确定滤波器第一部分的参数,接着计算滤波器第二部分的参数。其过程取决于滤波器极点的类型。本设计选取复数极点。
⑥选择合适的自然频率ωs和阻尼因子ζs。
ζs的最优值为ζs=0.707。经验表明,如果ωs=5ωT,则可以获得足够的相位裕度,所以设定:
至此,将上述所求参数代入式(6.12),得到
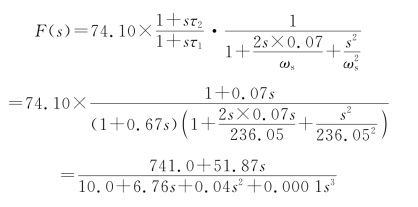
以上设计的锁相环可用于系统中,以提高系统的可靠性。