8.3.3 结合BP网络与ARMA模型的预测算法的设计与仿真
为了对最佳点火时刻进行预测,这里设计一种新的算法。我们将反向传播(BP)神经网络与自回归滑动平均(ARMA)模型结合起来,发挥BP神经网络的非线性映射能力与ARMA模型回归分析的精确性。其结构如图8.16所示。
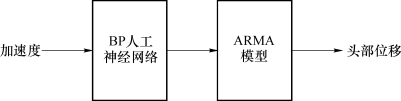
图8.16 算法结构图
算法分为两个大的步骤,首先是通过BP人工神经网络将加速度数据映射至30 ms后的位移数据的时间轴,之后再依据得到拟合的时间量与头部位移数据进行ARMA建模。其中,BP网络输入节点为5个,输出层节点为1个,隐含层为2层,第1层10个节点,第2层5个节点,传输函数采用双曲正切S形函数。输入的数据是当前时刻算起的之前最近10 ms的加速度值,采样周期为2 ms,即每次输入1个由5个数据组成的向量。而ARMA模型采用赤池信息量准则(Akaike Information Criterion,AIC)定阶,并用最小二乘法估计模型参数。下面对该算法进行仿真验证。
图8.17为某车型实际台车碰撞试验得到的两条不同碰撞强度(碰撞初速度)下的加速度曲线样本。其碰撞强度分别为碰撞初速度32 km/h和碰撞初速度56 km/h的正面碰撞。图8.18为与之对应的头部位移曲线样本。
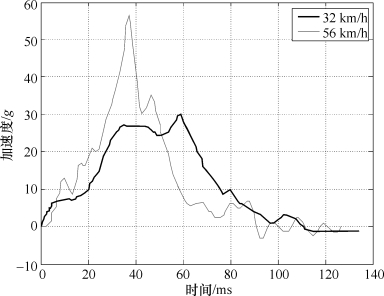
图8.17 加速度曲线
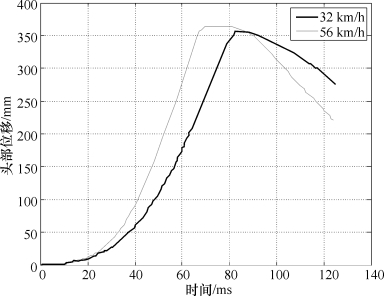
图8.18 头部位移曲线
按照算法,我们需要首先将加速度数据映射至时间轴,之后再对头部位移进行建模。
对于32 km/h、100%偏置情况,由于头部位移达到127 mm的时刻在53 ms附近,所以将附近区段作为考查目标,这里选取区间[44 ms,63 ms]的头部位移量。在加速度数据的选取上,由于是用当前时刻加速度值与之前10 ms内的加速度均值两个量对30 ms后的头部位移进行预测,所以选取区间[4 ms,33 ms]上的加速度数据,对区间[14 ms,33 ms]的每个数据计算之前10 ms的均值,并与该数据构成对应当前时刻的矢量数据,这样就得到了区间[14 ms,33 ms]上的输入数据矢量。首先将[14 ms,33 ms]上的数据矢量映射至时间轴[44 ms,63 ms]之上,之后再将时间轴拟合量作为ARMA模型的输入数据对区间[44 ms,63 ms]的头部位移量进行建模。这样我们得到的头部位移值与样本值对比图及其局部放大图分别如图8.19和图8.20所示。(https://www.daowen.com)
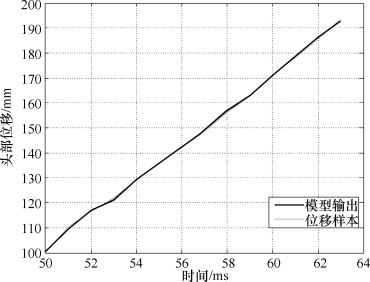
图8.19 32 km/h、100%偏置情况的网络输出值与样本值对比图
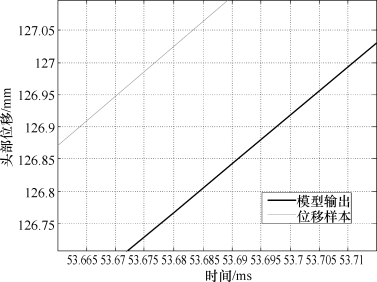
图8.20 32 km/h、100%偏置情况的网络输出值与样本值对比局部放大图
对于56 km/h、100%偏置情况,由于头部位移达到127 mm的时刻在44 ms附近,所以将附近区段作为考查目标,这里选取区间[35 ms,54 ms]的头部位移量。如前所述,由于是用当前时刻加速度值与之前10 ms内的加速度均值两个量对30 ms后的头部位移进行预测,所以选取区间[0 ms,24 ms]上的加速度数据,对区间[5 ms,24 ms]的每个数据计算之前10 ms的均值(不够的计算截至0的区间内的均值),并与该数据构成对应当前时刻的矢量数据,这样就得到了区间[5 ms,24 ms]上的输入数据矢量。首先将[5 ms,24 ms]上数据矢量映射至时间轴[35 ms,54 ms]之上,之后再将时间轴拟合量作为ARMA模型的输入数据对区间[35 ms,54 ms]的头部位移量进行建模。头部位移的网络输出值与样本值对比图及其局部放大图分别如图8.21和图8.22所示。
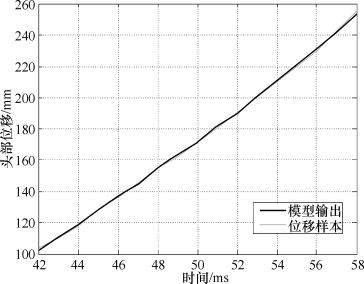
图8.21 56 km/h、100%偏置情况下头部位移的网络输出值与样本值对比图
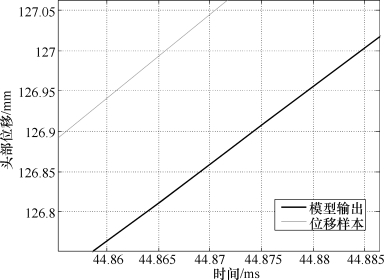
图8.22 56 km/h、100%偏置情况下头部位移的网络输出值与样本值对比局部放大图
如图8.19和图8.20所示,以样本头部位移曲线为参照,一方面,头部位移达到127 mm的时刻为53.675 ms,此时模型预测的头部位移为126.75 mm,误差为0.25 mm;另一方面,模型预测的头部位移达到127 mm的时刻为53.71 ms,即预测的最佳点火时刻为23.71 ms,与实际最佳点火时刻的误差为53.71-53.675=0.035 ms。对于图8.21和图8.22,以样本头部位移曲线为参照,一方面,头部位移达到127 mm的时刻为44.865 ms,此时模型预测的头部位移为126.8 mm,误差为0.2 mm;另一方面,模型预测的头部位移达到127 mm的时刻为44.885 ms,即预测的最佳点火时刻为14.885 ms,与实际最佳点火时刻的误差为44.885-44.865=0.02 ms。分析表明,网络预测的头部位移和样本位移有很好的拟合度,网络能够以极小的误差预测到乘员的头部位移量,从而给出精确的最佳点火时刻。
