5.2.4 恒流充电实现条件
第2章已经分析过恒流充电过程可使电容充电回路效率最大化。该特性的实现也是评价一个电容充电电源变换器性能好坏的重要标准。下面本书详细分析变换器实现恒流充电的条件。
1.倍压整流电路导通角分析
电容充电电源与普通直流电源工作过程不同,前者的输出电压是随着变换器工作周期增加而呈阶梯状上升。这里记第m个工作周期,对应的二极管导通角、谐振电流最大值和初始输出电压分别为θm、I rm(m)和U L(m-1)。
联立式(5.1)~式(5.3)可得

这里ω=2πf。
因此任意第m个周期流经二极管D2的平均电流值为
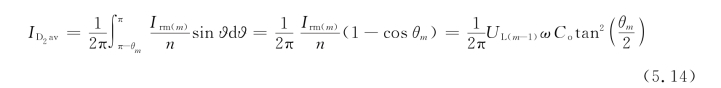
则在该周期中流入高压电容的电量为

假设电容充电过程实现线性恒流充电,忽略负载分压电阻消耗电能,由第m个周期流入电容的电量等于第m+1个周期的流入电量,有
![]()
将式(5.14)和式(5.15)代入式(5.16)中,有
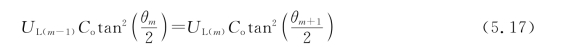
注意到:
![]()
由式(5.17)和式(5.18)可得满足恒流充电条件下,导通角变化的递推公式:
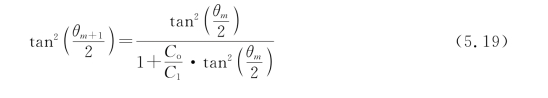
取θ的初始值为π,利用数值分析的方法由式(5.19)计算得导通角θ与运行周期数m的关系曲线,如图5.11所示,从图中看以看出随着充电周期的增加,导通角呈减小趋势。其中在开始的5 000个周期导通角下降较快,之后下降速度逐渐变缓,最后基本趋于稳定。(https://www.daowen.com)
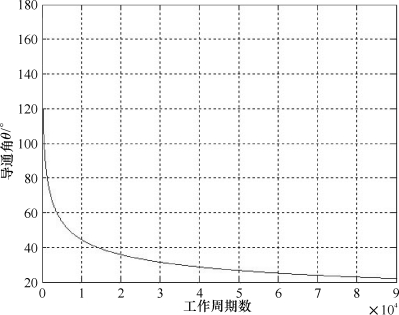
图5.11 导通角与工作周期数的关系曲线
2.恒流充电对支路谐振电流的要求
由式(5.13)可以得到,第m+1和第m个工作周期的谐振电流满足关系:
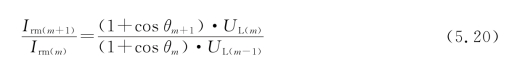
当变换器对高压电容实现恒流“等台阶”充电时,显然有
![]()
此时,对应的θm+1与θm的关系可由式(5.19)确定,定义系数:

联立式(5.19)和式(5.22)进行数值计算,可以得到变换器的工作周期数与系数k的对应关系曲线,如图5.12所示。
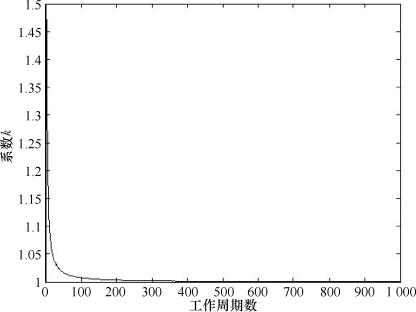
图5.12 工作周期与系数k的对应关系曲线
由图5.12可以得到,随着工作周期的增加,系数k逐渐减小并趋于恒定值(等于1),当工作周期大于60时,k的取值已小于1.01。通常电容器充电初期具有很好的恒流特性,本书设计的充电电源变换器工作周期约数万个,所以考虑整个过程实现恒流“等台阶”充电的条件时,本书取k=1。
所以由式(5.20)可得,实现恒流充电时,谐振电流的最大值应满足:

记ΔI rm(m)=I rm(m+1)-I rm(m),则有
![]()
由上式可知,当谐振电流的最大值满足起始值较小而后逐渐呈等台阶增大时,变换器便可以近似实现电容的等台阶充电。
