Fe—C系中渗碳体与石墨在α—Fe中的溶解度

一、Fe—C系中渗碳体与石墨在α—Fe中的溶解度

（一） 渗碳体在α—Fe中的溶解度

“渗碳体在铁中的溶解度”一般理解为：碳的溶解极限，当超过此溶解极限时，过量的碳则以碳化铁作为平衡相呈现；而 “石墨溶解度”则理解为：碳的溶解极限，当超过此溶解极限时，过量的碳则以石墨作为平衡相呈现。对于出现碳化铁的情况的平衡条件为：

则平衡常数K用式（3-13）计算：

式中 αC（α-Fe）、αFe（α）、αFe3C——分别为C、α—Fe和Fe3C的活度。

由此：

式中 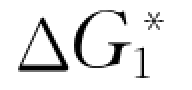——生成自由能；

R——气体常数；

T——绝对温度。

由于αFe3C和αFe实际上均为1，所以：

根据无限稀薄溶液，也就是说，根据亨利 （Henry）直线关系，如果在含碳量很少（最多为0．025%）的情况下，取αC= [C]（质量分数，%），则：

并且根据热力学第二定律：

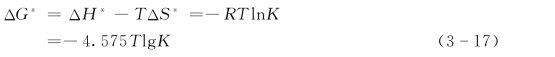
所以，

式 （3-17）、式 （3-18）中 ΔH*——热焓的变化；

ΔS*——熵的变化。

因此，

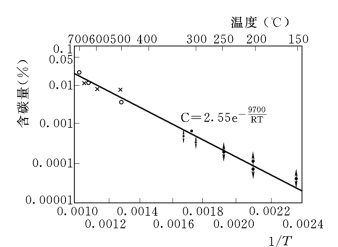
图3-4　由许多试验结果得出的渗碳体在α—Fe中溶解度随温度的变化

由此可以得知，碳在α—Fe中的溶解热为9700cal^[2]。

表3-2　渗碳体和石墨在α—Fe中的溶解度

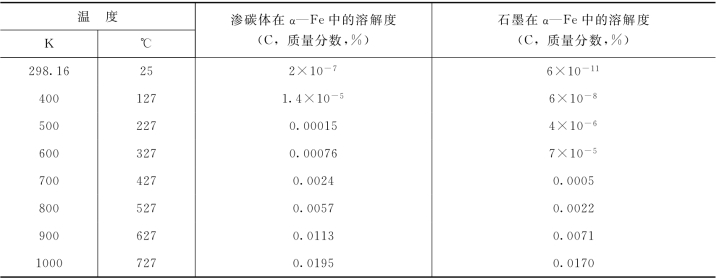
（二） 石墨在α—Fe中的溶解度

石墨与α—Fe之间的平衡，可以式（3-21）、式 （3-22）表示：

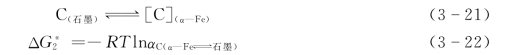
由Fe—C相图得知，碳在α—Fe中的溶解度很小。α—Fe—γ—Fe—石墨共析温度为738℃。在此温度时，碳在α—Fe中的溶解度大约为0．023%。根据L.Darken和R.Gurry关于渗碳体在α—Fe中溶解度的已知数据，可以对此进行计算。由式 （3-21）代入式（3-12），可以得出式（3-23）：

与此相对应，自由能的变化为：