Fe—C—X合金系

式中 m——以摩尔分数表示的比例系数。
如果碳的溶解度之差以质量分数ΔCX表示,则:
![]()
式中 Cmax——以质量分数表示,Fe—C合金中的碳溶解度;
CXmax——以质量分数表示,Fe—C—X合金中的碳溶解度;
ΔCX——以质量分数表示,由于附加合金元素X,使碳溶解度产生的变化。
并且,
![]()
式中 m′——以质量分数表示的比例系数,对于附加元素含量较低的情况来说,它是常数;
X——附加元素X的质量分数。当ΔCX 为正值时,X元素使碳的溶解度增加,如Mn、Cr、Mo、W、V、Ti等,当ΔCX 为负值时,X元素使碳的溶解度降低,如Si、Al、Ni、Cu、Co、Zr、P、S等。
对于Fe—C—S;—Mn—S—P成分的液态合金来说,碳的饱和浓度为:
![]()
例如,已知w(Si)=2.0%,w(Mn)=0.6%,w(S)=0.1%,w(P)=0.1%;又知m′Si=-0.317,m′Mn=0.027,m′P=-0.33,m′S=-0.36。
由此:
Cmax=1.30+2.57×10-3t-2.0×0.317+0.6×0.027-0.1×0.36-0.1×0.33=0.6132+2.57×103t℃
在共晶温度为1154℃时
![]()
亦即,此时的共晶碳饱和浓度为3.57%。
关于各种合金元素对液态Fe—C合金中碳溶解度的影响,已有许多研究工作发表。现可以归纳如下:
(一) 增加碳溶解度的元素
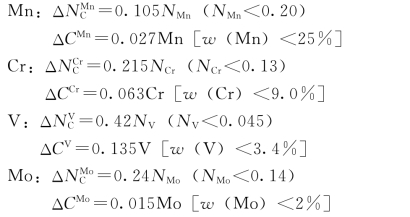
(二) 减少碳溶解度的元素
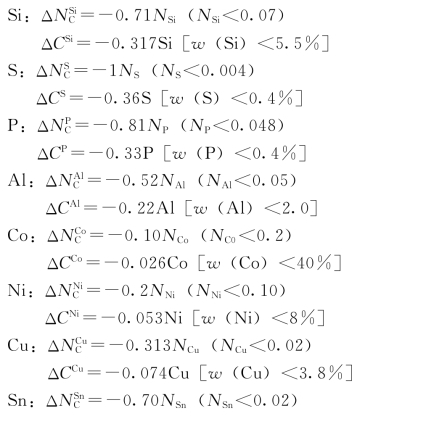
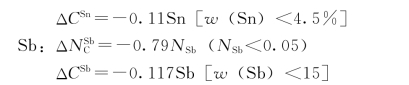
各种合金元素对液态Fe—C合金中碳溶解度的影响,示于图3-8。
图3-8 (a)是各种合金元素的摩尔分数与碳溶解能力的变化关系,此图清晰地示出单个合金元素之间的对比。ΔNCX 负值表示由于加入该合金元素后使碳在铁中的溶解能力变小,反之,ΔNCX 为正值则表示由于加入该合金元素后使碳在铁中的溶解能力变大。当含硅量较高时,随温度的不同,存在着硅与碳的饱和极限,超过此极限将有碳化硅 (SiC)沉淀析出。图3-8 (b)则是各种合金元素的质量分数与碳溶解能力的变化关系。
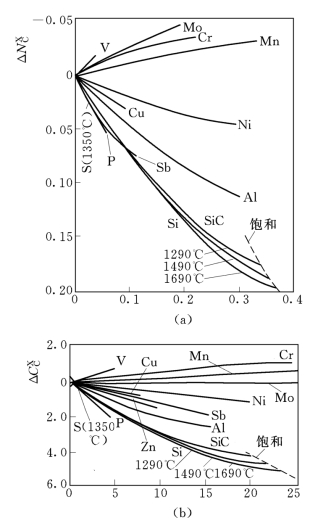
图3-8 各种合金元素对液态Fe—C合金中碳溶解度的影响
(a)以摩尔分数NX表示;(b)以质量分数CX表示
业已指出,附加合金元素可以提高也可以降低碳在铁中的溶解度。此时,合金元素对于碳在铁中的活度的影响,具有严格的关系。用碳的活度aC 可以定量地给出相应成分合金的物理化学行为;知道这个数值就可以表达碳与其他材料能发生反应的能力或者表达合金在冷却过程中沉淀析出石墨和碳化物的倾向。这对于铸件生产来说是极为重要的。
基体组织在很大程度上决定了铸件的力学性能、化学性能和物理性能。基体组织是由凝固和冷却过程所决定的,而这又与冷却条件、晶核条件及化学成分有关。根据冷却条件和晶核条件的不同,组织的细化程度和石墨形态可以在很宽广的范围内波动。改变化学成分就会以不同的方式影响凝固过程的进行和基体组织的变化,这或者是有新相的沉淀析击;或者使相区的范围移动,这往往是通过合金元素的加入而改变了碳的物理—化学行为所致。这有很重要的作用,因为Fe—C合金既可以按照稳定系统也可以按照亚稳定系统进行凝固过程。因此,提高碳的物理—化学行为,也就是提高碳的活度,就能使析出石墨的能力提高。否则,如果加入某种合金元素是降低碳的活度,则就使Fe—C合金中的碳化物稳定。
例如,硅能提高碳的活度,提高碳以石墨形式析出的能力,并使碳在铁中的溶解能力降低,因而硅使Fe—C相图中的C′点位置左移。如果合金元素形成碳化物的能力比铁还要大时,则这些合金元素就可提高碳在铁中的溶解能力。由此,使Fe—C相图中的C′点位置右移。
系数m和m′表明某元素X对碳溶解能力的作用,这种作用还与元素周期表密切相关。图3-9 (a)、(b)示出m 和m′与元素周期表序数的关系。正如图3-9 (a)所示,根据摩尔分数计算得出的系数m值,在每个周期(每族)里,与其原子序数呈直线排列。并且,第Ⅳ族与第Ⅴ族彼此呈平行走向;第Ⅵ族虽然不是实测值,但它也是与第Ⅳ、第Ⅴ族呈平行走向,同样,第Ⅱ族和第Ⅲ族的直线也是彼此平行的。
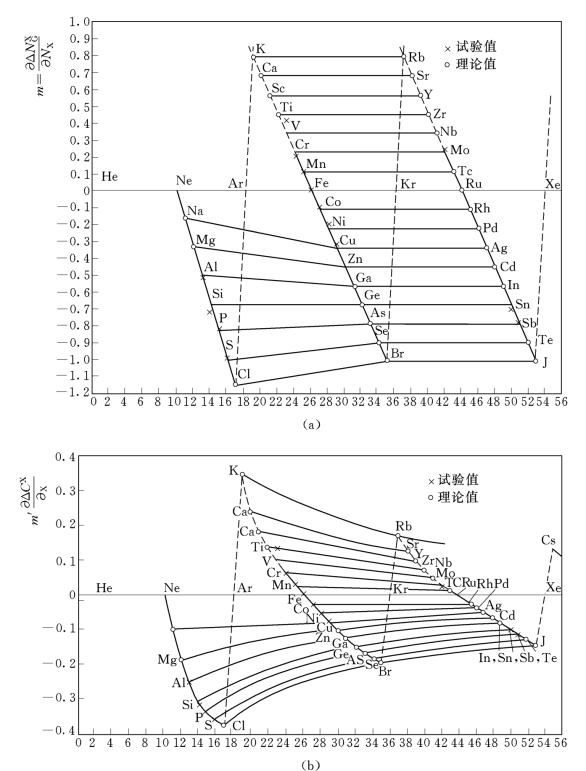
图3-9 比例系数m和m′与元素周期表的关系
(a)以摩尔分数表示m值;(b)以质量分数表示m′值
还要指出的是,属于周期表中某一族的元素对于碳的物理化学行为是相同的。只是在由第Ⅲ族过渡到第Ⅳ族时出现了突变。虚线具有特殊的意义,这是因为它表明,对于某元素来说,其作用与碳相比是没有区别的。
在严格的科学讨论时,必须用摩尔分数表示浓度。但是因为用摩尔分数进行计算是很麻烦的,所以,大多采用质量分数表示碳的浓度。因此,推导出以下公式,把用摩尔分数表示的m值换算成用质量分数表示的m′值。
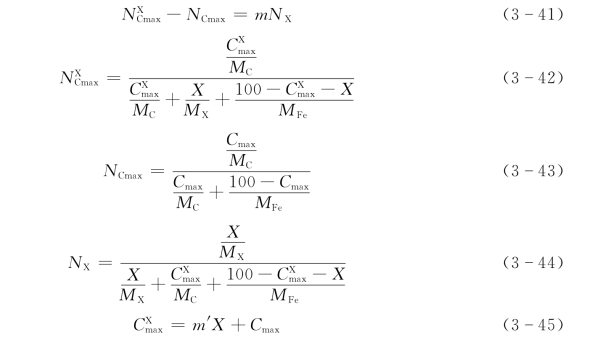
上述公式适用于所有的三元系,在m与m′之间有如式(3-46)所示关系:
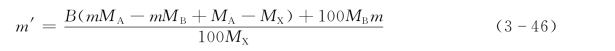
式中 A——指溶剂(这里指铁);
B——指溶质(在Fe—C系中碳的饱和浓度);
X——合金元素;
M——摩尔质量。
由图3-9 (b)可以看出,若以质量分数表示m′值时,则m′值与元素周期表的关系显示,各族元素之间不再呈明显的平行直线关系,由此表明,在进行理论分析时,以摩尔分数表示m值,则具有优越性。
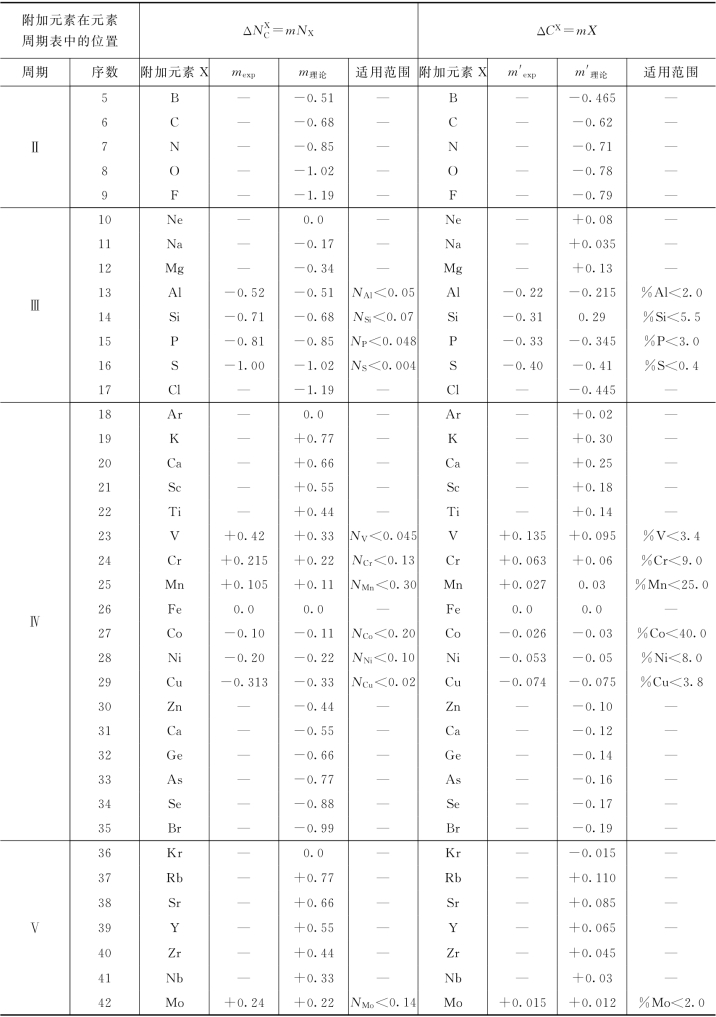
现把各种合金元素的比例系数m 和m′值列举在表3-3中,试验测得的数值分别以mexp和m′exp表示。表3-3中的m理论和m′理论表示理论预测的比例系数,表3-3中还列举了各相应元素的适用范围。对比分析表明,理论预测与试验测得的数值符合得很好。
表3-3 附加元素对碳在铁液中溶解度的影响
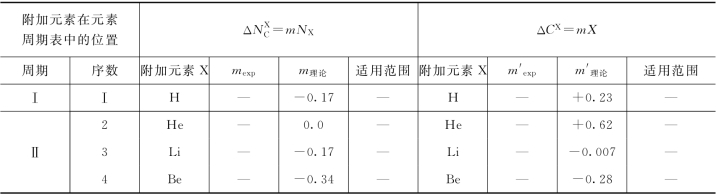
续表
续表
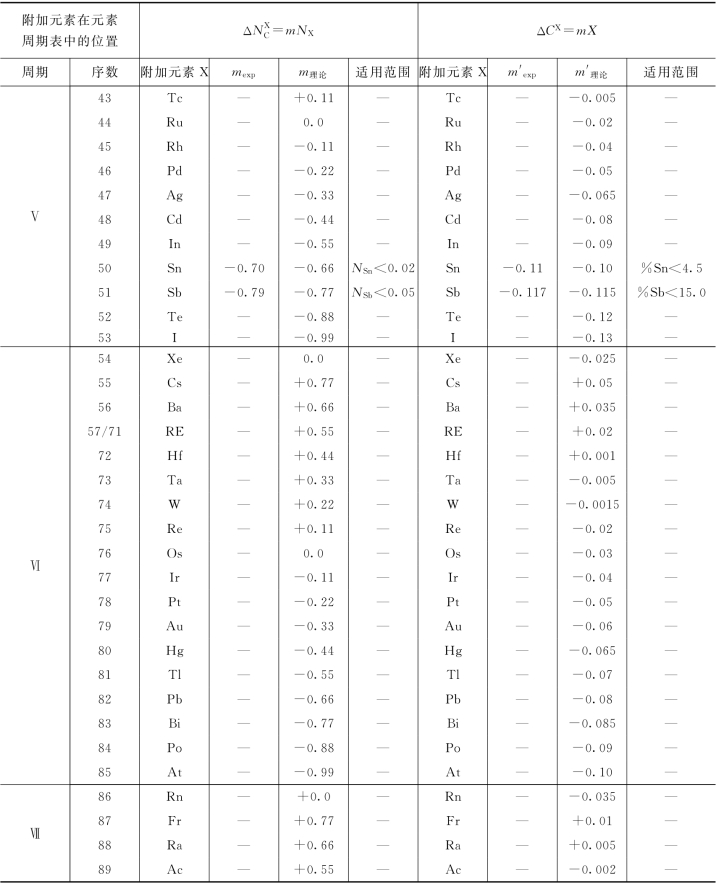
注 表中mexp、m′exp是由试验得知;m理论、m′理论是理论值。
【注释】
[1]1cal=4.1868J
[2]1cal=4.1868J
