引言
本书基于作者在过去15年间在各种相关课程上的讲稿讲义.这些讲稿所包含的材料由两位作者在华东师范大学,英国帝国理工大学,牛津大学,复旦大学等学校的各层次的课堂上多次授课,这些材料特别地为随机分析,随机模型,数理金融等那些为了对It
微积分以及其中的一些计算技巧有所了解的从业者所欢迎.
一个随机微分方程是带有随机扰动(其强度依赖于对象的时间与位置)的微分方程,其形式如下
概率论的中心极限定理提示˙Wt应该具有正态分布,且为了简单起见,应该在不同的时间点是独立的.这样的随机扰动可以理想地用Brown运动来作为模型,所谓Brown运动是描述花粉在液体中的移动所建立的数学模型,作为一种生物现象,它是由植物学家R.Brown首先观察并描述下来的,Brown运动的数学形式及其分布是由A.Einstein在一篇发表于1905年Annalen der Physik 17,549-560的题为“On the motion of small particles suspended in liquids at rest required by the molecular-kinetic theory of heat”的论文中导出的.大约在同时,1900年,L.Bachelier递交了他的题为“Th´eorie de la sp´eculation”的博士论文,其中使用了Brown运动来模拟股票市场,他的结果发表在Ann.Sci.Ecole Norm.sup.,17(1900),21-86,被认为是第一篇将Brown运动应用于金融的论文.
然而,Brown运动的一个数学构造或者说Brown运动的轨道连续性是在1923年由美国数学家N.Wiener在其论文“Diあerential space”,J.Math.Phys.2,132-174中完成的,有关Brown运动的丰富多彩的结果以及不寻常的性质是由P.L´evy在上个世纪的30到40年代所揭示的,其中L´evy证明了Brown运动的几乎所有轨道是无处可微的,因此其关于时间的导数˙Wt在通常意义下不存在,故而我们有必要将前面的随机微分方程重新写成为
它必须被解释为下面的积分方程
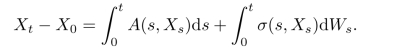
也就是说,我们需要定义类似
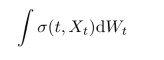
形式的积分,它显然也不会在通常意义下存在.K.It
在1940年代首次为Brown运动建立了积分理论,因此建立了随机微分方程的理论,除了在其他数学领域的应用,It
理论的最近的最为辉煌的应用是在金融理论领域.尽管It
本人并没有获得Fields奖,但他的名字由于许多应用It
微积分理论的杰出工作获得Nobel奖的经济学家(例如1990年的H.Markowitz,W.Sharpe and M.Miller,1997年的Robert Merton,and M.Scholes)而被世人熟知.
本书的基本框架基于第一位作者在牛津大学讲授该课程时的讲义,第二位作者根据在复旦大学的教学所需补充或者改写了一些内容,并添加了习题.本书所覆盖的内容为那些对随机模型及其在金融随机控制等领域的应用感兴趣的人提供了必要的随机分析知识,且对那些专修纯粹数学如分析,微分几何,泛函分析,调和分析,数学物理以及偏微分方程等方向的学生也有很好的参考价值.感谢修读此课程的许多同学,指出了书中存在的很多错误.感谢复旦大学研究生院的资助,同时感谢研究生院先梦涵老师的支持,最后要感谢复旦大学出版社的陆俊杰编辑,他仔细阅读书稿并改正了其中很多文字错误.
钱忠民University of Oxford,UK
应坚刚复旦大学