§4.5　习题与解答

§4.5　习题与解答

1.设M是连续局部鞅.证明:M≡M0当且仅当〈M〉≡0.

5.设Z是有界随机变量,A是从0出发的有界连续增过程.证明:

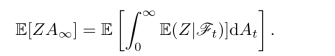
6.设M是连续局部鞅.证明:M2具有二次变差过程且

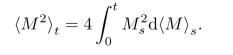
7.设M是Gauss过程且是连续鞅,证明:〈M〉是确定性过程(只与时间有关).

8.设M是连续局部鞅,K∈L2(M),ξ是Fs可测随机变量.证明:对t＞s≥0,

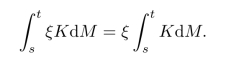
9.如果M是连续局部鞅,M0=0,

(a)证明:如果〈M〉T可积,那么M=(Mt:t∈[0,T])是平方可积鞅;

(b)证明:M在{supt〈M〉t＜∞}上当t趋于无穷时几乎处处收敛.

证明.取局部化序列使得Mτn,(M2-〈M〉)τn都是有界连续鞅,那么

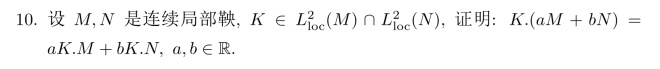
11.用归纳法验证:对连续半鞅X,有

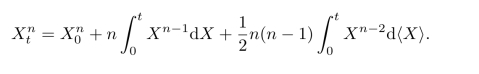
12.设f是[0,T]上连续函数(与ω无关),证明:f=(f(t))是连续半鞅当且仅当f连续且有界变差.

其中ξ是有界Fσ可测的,则K.M=ξ(Mτ-Mσ);

(b)证明:〈M〉σ=〈M〉τ当且仅当M在[σ,τ]上是常值.