§6.2.1 线性Gauss扩散
2026年01月14日
§6.2.1 线性Gauss扩散
线性随机微分方程可以被显式地解出来.考虑
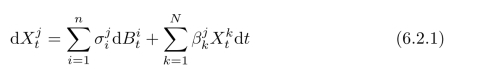
(j=1,···,N),其中B是一个n-维Brown运动,σ=(σji)是常数N×n矩阵,β=(βjk)是常数N×N矩阵.(6.2.1)可以写成为
![]()
设
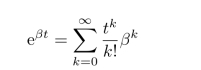
是方阵β的指数.应用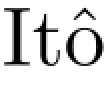 公式,我们有
公式,我们有
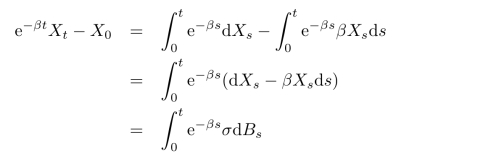
因此
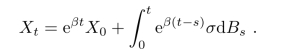
特别地,如果X0=x,那么Xt是均值eβtx的正态分布.例如,若n=N=1,则
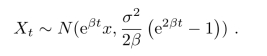
可以证明(Xt)是扩散过程(即连续的马氏过程),其转移概率函数p(t,x,z)为
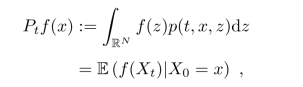 (https://www.daowen.com)
(https://www.daowen.com)
因此

故
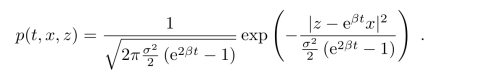
为了证明(Xt)是Markov过程,我们需要验证
![]()
是转移函数,即满足Chapman-Kolmogorov方程
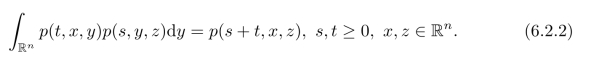
练习6.2.1 验证p(t,x,y)满足Chapman-Kolmogorov方程.
练习6.2.2 很容易从上面的表达式看出
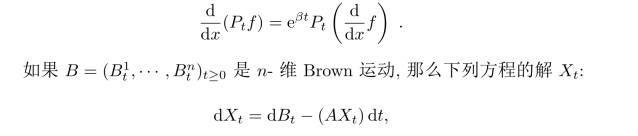
其中A≥0是d×d矩阵,称X为漂移矩阵A的Ornstein-Ulenbeck过程.且有
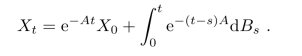
练习6.2.3 若X0=x∈Rn,计算Ef(Xt),其中Xt是漂移矩阵为A的Ornstein-Uhlenbeck过程.
