§1.5　习题与解答

§1.5　习题与解答

1.(Kolmogorov 0-1律)设ξ1,···,ξn,···是独立随机变量序列,令

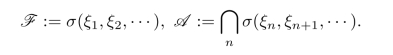
证明:F与A独立,且对任何A∈A,P(A)=0或1.

3.设ξ是随机变量,证明:ξ与子σ-代数A独立当且仅当对任何有界Borel可测函数g有E[g(ξ)|A]=E[g(ξ)],也等价于对任何x∈R有

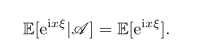
4.设{Fα:α∈Σ}是一个子σ-代数族,证明:若ξ是可积随机变量,则{E[ξ|Fα]:α∈Σ}一致可积.

5.对两个可积且乘积也可积的随机变量ξ,η证明:E[ξE[η|A]]=E[ηE[ξ|A]].

6.设X,Y独立可积且EX=EY=0,证明:E[|X|]≤E[|X+Y|].

7.设ξ,η为可积随机变量且E[ξ|η]=η,E[η|ξ]=ξ,证明:ξ=ηa.s.

8.设(ξt:t∈I)是概率空间(Ω,F,P)上随机变量族,证明:对任何A∈σ(ξi:i∈I),存在可列子集S⊂I使得A∈σ(ξi:i∈S).

9.设(ξt:t∈I)是概率空间(Ω,F,P)上随机变量族,ξ是可积随机变量.证明:存在可列集S⊂I使得