§6.2.3 Cameron-Martin公式
2026年01月14日
§6.2.3 Cameron-Martin公式
考虑简单随机微分方程

其中b(t,x)是[0,+∞)×R上有界Borel可测函数.我们可以用概率变换的手段解方程(6.2.4).
设(Wt)t≥0是(Ω,F,Ft,P)上标准Brown运动,定义(Ω,F∞)上概率测度Q为
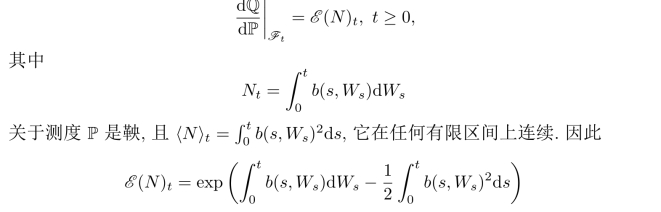
是一个鞅(是局部鞅,需要适当的条件成为鞅).按照Girsanov定理
![]()
在新测度Q下是鞅,且〈B〉t=〈W〉t=t.由L´evy的鞅刻画定理推出(Bt)t≥0在测度Q下是Brown运动.进一步,
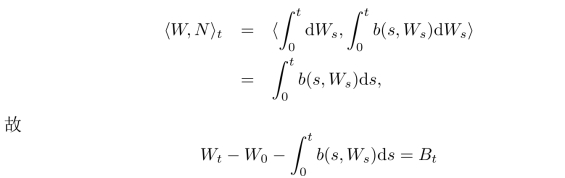 (https://www.daowen.com)
(https://www.daowen.com)
是(Ω,F,Q)上标准Brown运动.因此
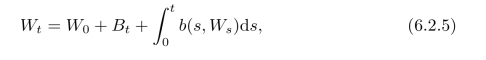
那么(Ω,F∞,Q)上的(Wt)t≥0是(6.2.4)的解.这个解是随机微分方程(6.2.4)的一个弱解.
定理6.2.1 (Cameron-Martin-Girsanov)设

的解.

我们可以证明(Xt)t≥0在概率测度˜P下是Brown运动.因此方程(6.2.6)的解有分布唯一性:其所有解同分布.
