§6.4　强解:存在唯一性

§6.4　强解:存在唯一性

在本节中,我们将介绍强解存在唯一性的基本结果.由定义,强解必是(弱)解.我们将证明在系数满足整体Lipschitz条件下的一个存在唯一性结论,证明基于两个不等式:Gronwall不等式与Doob的Lp-不等式.

引理6.4.1　(Gronwall)如果一个非负函数满足积分方程

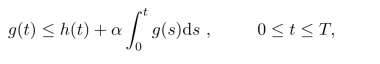
其中α≥0是常数且h:[0,T]→R是可积函数,那么

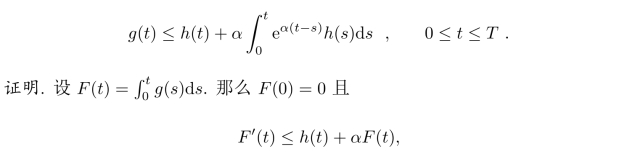
故

对这个微分不等式积分,我们得到

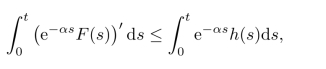
因此有

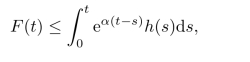
这推出Gronwall不等式.

考虑下面的随机微分方程

引理6.4.2　设(Bt)t≥0是(Ω,Ft,F,P)上实值标准Brown运动,且(Zt)t≥0与(˜Zt)t≥0是连续适应过程.设f(t,x)是一个Lipschitz函数

其中C是常数.

(1)如果

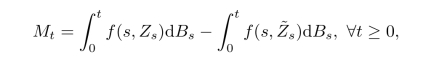
那么

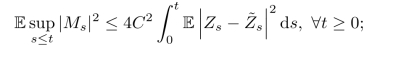
(2)如果

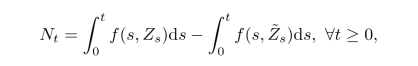
那么

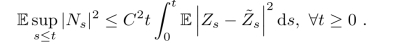
证明.为证明第一个结论,我们注意到

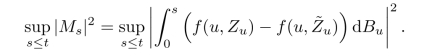
由Doob的L2-不等式,

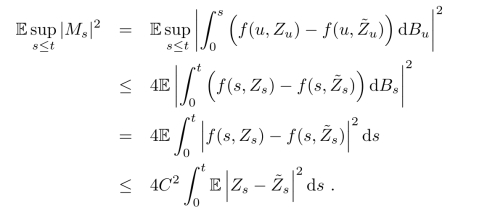
接着证明第二个结论.事实上,

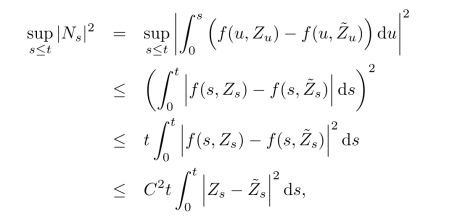(https://www.daowen.com)

然后第二个不等式由Schwarz不等式推出.

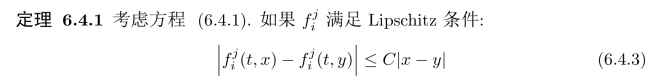
与线性增长条件

如同常微分方程一样,我们通过Picard迭代构造逼近解:

且

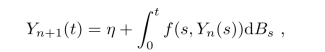
其中n=0,1,2,···.我们将证明对任何T＞0,序列{Yn(t)}在[0,T]上一致地几乎处处收敛于一个解Y(t).注意到每个Yn都是连续平方可积鞅,故我们有

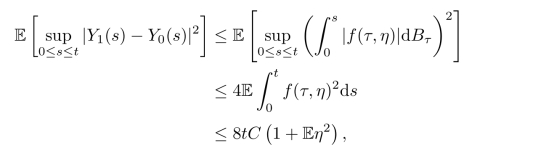
且对任何t≤T,

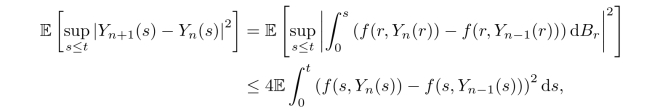
其中第二个不等式来自Doob的不等式.因为f是Lipschitz连续的,故而

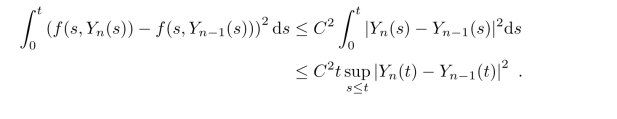
结合前面的不等式,我们得到对任何t≤T,有

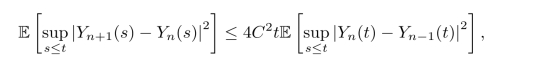
因此对任何t≤T,

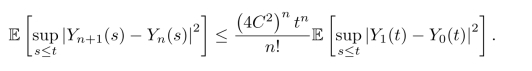
特别地有

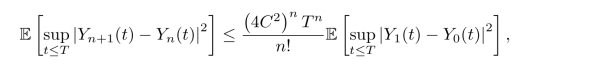
这可以推出

下面我们证明唯一性.设Y与Z是同一个Brown运动下的两个解,那么

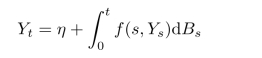
且

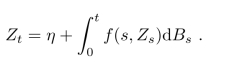
如同在存在性的证明中那样,

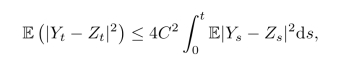
由Gronwall不等式推出

注释6.4.1　.定理6.4.1　中构造的迭代Yn是Brown运动的函数,或者说Yn(t)仅依赖于初值η与(Bs:0≤s≤t).