§4.1　引论

§4.1　引论

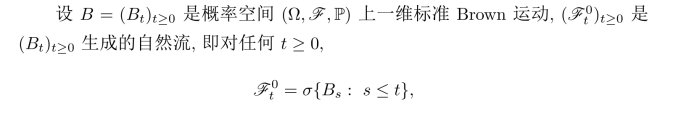
它表示Brown运动B=(Bt)t≥0直至时间t的历史.加入所有零概率集之后记为(Ft).

我们的主要目的是定义下列形式的It积分

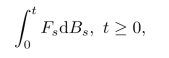
其中被积过程F=(Ft)t≥0是满足某些条件(后面详解)的一个随机过程.例如,我们可以对Borel可测函数f定义积分

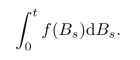
考虑[0,1]上的两个函数f,g,D是[0,1]上一个分划,定义

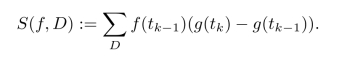
一个众所周知的分析结果说,如果对任何连续函数f,当D趋于零时,S(f,D)收敛,那么函数g在[0,1]上必定是有界变差的.

练习4.1.1　证明这个结论.提示:应用共鸣定理.

反过来说,如果g不是有界变差的,那么以上和式不可能对所有连续函数收敛.因为对几乎所有的ω∈Ω,Brown运动的样本轨道t→Bt(ω)在任何区间上都没有有界变差,故按样本轨道的Riemann和形式

仍然是一个随机过程,当有限分划趋于零时,对于任何固定的t,它是下面特殊的Riemann和的极限:

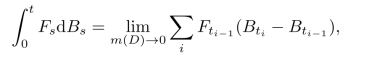
其中极限的存在可能在L2-意义下,但更一般地,是在依概率收敛的意义下,另外分划趋于零是指

满足m(D)=maxi(ti-ti-1)→0.选择左端点的理由是:只有这样选择,才有

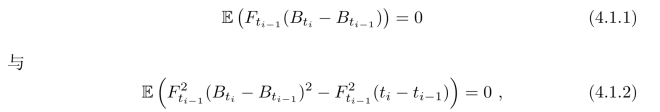
从而使得随机积分代表的随机过程F.B是一个鞅.不仅如此,更重要地,类似Brown运动,其平方后减去一个增过程得到的过程

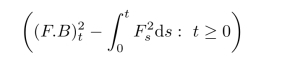
也是一个鞅.

我们由此得到所谓的It等距映照

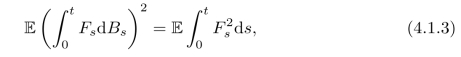
固定时间T,[0,T]上的鞅(Mt)是由其终端值MT所唯一决定的.它意味着映射

随机积分将先对于简单随机过程定义,然后利用It等距进行扩张,对更一般的随机过程定义,之后利用局部化技术扩张到局部有界过程关于连续局部鞅的积分,最后扩张到关于连续半鞅的积分.