1.1 物理量的测量和实验误差
物理学是一门实验科学。 物理实验就是要把自然界中物质的运动形态按人们的意愿在预定的条件下,以比较纯粹或典型的形式再现,从而使人们有可能在较有利的条件下,探索各相关量之间的规律性或验证理论。 因此,物理实验中基本的操作就是测量。
1.测量与测量分类
测量是指将待测量与规定为基本单位的物理量进行比较,其倍数即为待测量的大小,其单位就是与之进行比较的基本单位。 例如,我们说测得某桌子的长度为1.248 m,则表示基本单位为m,而桌子的长度为基本单位的1.248 倍(数值),显然数值的大小与选用的单位有关。因此,我们在给出某一待测量的结果时,必须同时给出数值和单位,两者缺一不可。 实际的测量过程一般要借助测量仪器,测量仪器是指用以直接或间接测出被测对象量值的所有器具。如游标卡尺、天平、停表等,测量仪器是基本单位的实物体现。 测量通常分为直接测量和间接测量两类。 直接测量就是待测量与仪器直接比较,得出被测量量值的测量。 例如,用米尺测量物体长度,用天平测量物体质量等。 但在物理实验中,还有一些物理量不能直接从仪器上测得,而要通过对某些相关物理量的直接测量,再根据相应的公式计算出被测量的大小,这种测量称为间接测量。 例如在单摆实验中,通过对摆长l 和周期T 的测量,由公式![]() l 计算出重力加速度g 的过程就是间接测量。
l 计算出重力加速度g 的过程就是间接测量。
2.误差及其分类
任何被测量在一定的条件下都客观地存在一个唯一的确定值,该值称为被测量的真值。测量的目的就是获得真值。 但是由于实验条件、实验方法、实验仪器和实验者自身判断等,任何测量都不是绝对“准确”的,测量者总希望测量结果尽可能准确,甚至幻想获得绝对准确的真值,而真值恰恰是不可能测量到的。 随着测量技术的不断进步,测量结果会根据需要有限度地接近真值。 实践中,可把相对可靠、准确度足够高的实际测量值作为约定真值,例如国际数据委员会(CODATA)公布的物理量或常数、标准物质(如砝码)的值、标准器证书上的值、某物理量重在复性条件下多次测量的平均值等。
测量值与真值之间总存在差异,测量值与被测量真值之差称为绝对误差,记作δ,
![]()
式中X0 为被测量的真值,x 为测量值, δ 为该次测量的绝对误差值。 误差的符号借用了微分符号,其目的是强调误差是小量,并且可正、可负。
测量结果的相对误差

真值是一个理想的概念,一般无从得知,因此,通常情况下不能计算误差。 只有在极少数情况下,相对可靠、准确度足够高的实际测量值被视为约定真值时,才能计算误差。
从误差自身的特点和所服从的规律考虑,误差主要分为系统误差、偶然误差两类。 它们的性质不同,应分别予以处理。
(1)系统误差
在对同一被测量的多次测量过程中,实验系统存在恒定的或以可预知方式变化的测量误差,该误差分量称为系统误差。 系统误差具有确定性,测量过程中要对系统误差进行正确分析,尽量发现和消除系统误差,提高测量结果的可靠程度。
系统误差主要来源于以下几个方面。
①仪器因素:仪器制造上的缺陷;仪器未经校准、使用不当等。 例如,量块的两面不平行;电表刻度线的间隔不等或径向磁场不均匀;数字表输入级线性放大器的零点或增益漂移等。
②理论、方法因素:测量所依据的理论、公式存在近似性;实验条件、测量方法不满足理论要求等。 如伏安法测电阻时电表内阻的影响。(https://www.daowen.com)
③人员因素:测量者生理或心理特点所导致的误差。 例如反应速度的快慢、分辨能力的高低、读数习惯等。
④环境因素:测量过程中温度、湿度、气压、振动、电源电压、磁场等因素的差异和变化。
系统误差又分为可定系统误差(可修正误差)和未定系统误差(不可修正误差),对于可定系统误差,一般情况下都能找到原因并事先修正。
可定系统误差容易被发现,应尽量避免,如无法避免,可有针对性地采用不同的方法予以减小或消除。 例如:
①测量前检查或校正零位。
②引入修正值对测量值进行修正。
③通过仪器的设计和测量方法的选择抵消系统误差的影响。
如仪器读数装置的对称设计;将测量中的某些因素(如被测物体)交换位置(交换法);在一定条件下用已知量代替被测量(替代法);改变测量的方向使产生的系统误差等值异号,然后求其平均作抵消(异号法)等。
未定系统误差一般难以消除,也不能进行修正,只能作为不确定度的一种分量进行合理的估算和评定。
在测量实践中,不可避免地要产生系统误差,而且系统误差是测量结果误差的主要分量,多数仪器的误差限值主要反映未定系统误差的影响。 如何在实践中分析系统误差是自然科学工作者和工程技术人员的一项重要任务。 因此,在大学物理实验中,我们要重视对系统误差的分析和处理,尽量减小它对测量结果的影响。
(2)偶然误差
在消除系统误差以后,对同一被测量在等精度条件下进行多次测量,仍然不会得到完全相同的结果,其测量值分散在一定的范围内,所得误差时正时负,绝对值时大时小,呈现出无规则的涨落,这类误差分量称为偶然误差。 偶然误差是由测量过程中的一些随机的或不确定的因素引起的。 如人的感官灵敏度、仪器精确度限制、周围环境的干扰以及随测量而来的其他不可预测的偶然因素等。 偶然误差具有随机性,也就是说,在相同条件下,对同一被测量进行多次重复性测量,每次测量值的误差可大可小,就某一次测量值来说,其误差的大小与正负都无法预知,纯属偶然。 但如果测量次数相当多的话,偶然误差的出现则服从一定的统计规律,通常在大学物理实验中,服从正态分布规律。 如图1.1 所示为正态分布曲线,其横坐标是测量值,纵坐标是每单位x 出现的概率,或称为概率密度。 其特点如下:
①单峰性:绝对值小的误差比绝对值大的误差出现的概率大。
②对称性:大小相等的正、负误差出现的概率均等,对称分布于真值的两侧。
③有界性:绝对值很大的误差出现的概率几乎为零,即误差的绝对值不超过一定的限度。
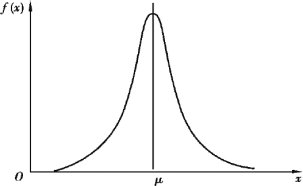
图1.1 正态分布曲线
