1.2 直接测得量的误差估算
在物理实验中,由于既有系统误差,又有偶然误差,并且它们的来源和处理方法又不相同,为了讨论方便,我们假设已消除了系统误差,或系统误差已减小到可以忽略的程度,即只按纯粹的偶然误差来处理。
1.直接测量结果的误差估算
(1)算术平均值——测量结果的最佳估计值
对某一物理量进行测量时,只要条件允许,总可以进行多次重复测量。 由偶然误差的特点可知,当测量次数无限增多时,由于正负误差相互抵消,多次测量的算术平均值的极限将趋于待测量的真值。 由于实际进行测量时,测量次数不可能无限多,假设对某量测了n 次,测得值分别为x1,x2,…,xn ,我们称这n 个值为一个测量列,其算术平均值为
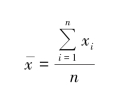
x 只是近似真值,通常称为“最佳估计值”或“最近真值”,测量结果就用最佳估计值表示。
(2)多次测量误差的估算
当用最佳估计值表示多次测量结果时,必须同时指出其误差大小。 关于误差的估算有多种方法,目前,国际上已统一采用统计学中的标准误差来评价偶然误差的大小。
①测量列的标准误差和标准偏差。
各测量值误差的平方和的平均值的平方根称为测量列的标准误差。 设某一测量列为x1,x2,…,xn ,真值为a,则各测量值误差为:ε1 = x1 - a,ε2 = x2 - a,…,εn = xn - a,则



式(1.4)即为用残差来估算标准误差的表达式,称为标准偏差(贝塞尔公式)。 对一个测量列而言,如果求得的标准偏差δs 小,即表示测量的精密度高。 同样根据统计理论,如果给定误差区间(-σs ,+σs ),则表示测量列中每一测量值的偏差在(-σs ,+σs )内的概率为68.3%。
②算术平均值的标准偏差。

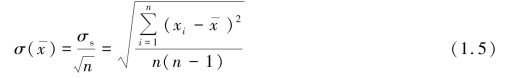
③测量结果的表示。(https://www.daowen.com)
当用标准误差进行误差估算时,待测量的结果可表示为
![]()

④绝对误差与相对误差。
在对某一物理量进行测量时,总可把测量结果表示为如下形式:
![]()
式中Δx 称为测量结果的绝对误差,它与待测量有相同的单位,其大小反映测量值偏离真值的程度。 绝对误差有不同的估算方法,除上面讲过的标准误差外,还有平均绝对误差、极限误差、或然误差等。 当然,不同的估算方法其概率不同。 用标准误差估算时,p=68.3%;用平均绝对误差估算时,p=57.5%;用极限误差估算时,p=99.7%;用或然误差估算时,p=50%。在对不同的测量结果进行比较时,绝对误差的大小还不能客观全面地评价测量的优劣。 例如,用不同仪器测量不同物体的长度时,得到如下结果:
![]()
如果单从绝对误差大小来看,Δl1 >Δl2,但从误差所占整个测量结果的比重来看,前者为0.5%,而后者为0.02%,说明前者的测量质量高。 所以在评价与比较不同的测量结果时,引入相对误差的概念是必要的。 相对误差的定义是测量结果的绝对误差与待测量真值(最近真值)的比值,常用百分数来表示,即
![]()
在表示测量的最后结果时,既要写出绝对误差,又要写出相对误差,在实验报告中最好写成如下形式:
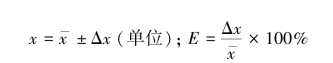
2.单次直接测量结果的误差估算
有些实验由于是在动态中测量的,不容许对被测量在相同条件下作重复测量。 例如,热学实验中的温度测量就无法多次测量。 另外在间接测量中,该物理量的误差对最后的结果影响较小或在有些实验中对精度要求不高,在这些情况下,对被测量只测一次,那么它的误差应如何估算呢? 对于单次测量,由于误差的来源很多,各个实验又有各自的特点,所以很难用统一标准。 目前一般按照如下两个约定:
①当测量的偶然误差可能较小时,通常取仪器的最小分度值为极限误差;
②当测量的偶然误差较大时,选取仪器的最小分度值的几倍为极限误差。 一般是取最小分度值为极限误δmax ,所以单次测量量的标准误差可估计为

