1.4 有效数字及其运算
实验数据的有效数字问题看似简单,其实不然,实验过程中要记录很多数据,实验后要对这些数据进行计算处理,以得出最终测量结果。 那么,记录时应取几位数字? 运算中间过程应保留几位数字? 最后的结果又应保留几位数字? 以上都是实验数据处理中的重要问题,应有一个明确的认识。
1.有效数字的概念
实验中所测得的量值都含有误差,因此不能任意取舍,写出的数值必须能够反映测量的准确度(不确定度)。
例如用钢直尺测量光杠杆的臂长,仪器的最小分度值为1 mm,能估计到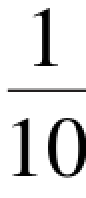
分度,测得值为31.3 mm,测量值共有三位,“31”是直接从直尺上读到的数字,称作准确数字,最末一位“3”是从测量仪器的最小分度之间估计出来的,称作欠准数字。 准确数字与欠准数字共同构成了测量值的有效数字。 所以,这个测量值的有效数字是31.3,有效位数有三位。
有效位数的多少是由测量仪器的精度和被测量量值的大小决定的,它直接反映出测量的准确程度。 实验中应该注意以下几个问题:
①对十进位数,从非零数字最左一位向右数而得到的位数,就是有效位数。
②有效位数与小数点的位置无关。 例如2.34 cm 改用m 作单位时为0.023 4 m,它们的有效位数都是三位。
③数字末尾的“0”不能随意取舍。 例如8 410 Ω 与8.41×103 Ω 不一样,前者有四位有效位数,而后者只有三位。
④常数的有效位数可根据需要恰当选择,一般以参与运算的各量中有效位数最多者为参照,多选一位(或选相等位数)。
⑤对很大或很小的数值,正确使用科学计数法,但要保证有效位数不变。 例如
2.有效数字的运算规则
有效数字运算的总规则是:准确数字与准确数字运算,结果仍为准确数字;准确数字与欠准数字运算,结果为欠准数字;欠准数字与欠准数字运算,结果为欠准数字;运算结果只保留一位欠准数字,其余的欠准数字按照有效数字的数值修约规则处理。
(1)加减运算
加减运算时,以参与运算的各项中末位数量级最大的那一位作为运算结果的有效数字的末位。
例如:30.3+1.318+0.002 7=30.3+1.32+0=31.6
(2)乘除运算
参与乘除运算的各项中,以有效位数最少的一项的有效位数,作为运算结果的有效位数。
(3)乘方、立方、开方运算
运算结果的有效位数与参与运算的数字的有效位数相同。
(4)函数运算
一般来说,函数运算结果的有效位数需要通过微分公式先求出不确定度,再由不确定度所在位确定有效数字的最后一位。 为了简便起见,按照以下规则处理:
①对数运算结果的有效数字中,小数点后的位数取成与真数的位数相同。
②指数函数运算结果的有效数字中,小数点后的位数取成与指数中小数点后面的位数相同。
③三角函数运算,所用三角函数表的位数随角度误差的减小而增加,角度误差为1′、10″、1″、0.1″时,相应的三角函数表位数分别选择4 位、5 位、6 位、7 位。
3.数值修约规则
有效数字的数值修约就是去掉数值中多余的欠准位。 我国标准(与大多数国家的标准基本一致)规定的《数值修约规则与极限数值的表示和判定》(GB/T 8170—2008),其要点如下:
①拟舍弃数字的最左一位数字小于5 时,则舍去,保留其余各位数字不变。
②拟舍弃数字的最左一位数字大于5 时,则进1,即保留数字的末位数字加1。
③拟舍弃数字的最左一位数字是5,且其后有非0 数字时进1,即保留数字的末位数字加1。
④拟舍弃数字最左一位数字为5,且其后无数字或皆为0 时,若所保留的末位数字为奇数(1,3,5,7,9),则进1,即保留数字的末位数字加1;若所保留的末位数字为偶数(0,2,4,6,8),则舍去。
⑤负数修约时,先将它的绝对值按上述规定(①—④)进行修约,然后在所得值前加上负号。
⑥修约过程应该一次完成,不能多次连续修约。 例如,要使0.546 保留到一位有效位数,不能先修约成0.55,再接着修约成0.6,而应当一次性修约成0.5。
例如,将下列数据保留3 位有效位数:9.824 99,9.825 71,9.825 00,9.825 01。
9.824 99,将要舍弃的部分“0.004 99”小于“0.005 00”,修约值为9.82;
9.825 71,将要舍弃的部分“0.005 71”大于“0.005 00”,修约值为9.83;
9.825 00,将要舍弃的部分“0.005 00”等于“0.005 00”,且“5”前面的数字是偶数“2”,则修约值为9.82;
9.825 01,将要舍弃的部分“0.005 01”大于“0.005 00”,则修约值为9.83。
这套规则可简单地叫做“四舍六入五凑偶”规则,从数学本质上看是为了避免当数据分散性比较大时,四舍五入过程中入的机会多一点,舍的机会少一点,由此而产生的系统性偏差。
4.实验数据有效位数的确定
知道有效位数后进行修约不难,因为规则较简单,难点在如何确定数据的有效位数。 数据读取和结果表示时,有效位数的确定是为了保证测量结果的准确度基本不会因位数取舍而受到影响,同时避免因多读取或保留一些无意义的多余位数而做无用功。
下面分别从读数、运算和结果表示三个环节来讨论如何确定有效位数的问题。
(1)原始数据有效位数的确定
由仪表、量具读取原始数据时,一般要充分反映计量器具的准确度,通常要使计量器具所能读出(包括估读)的位数全部读出来。
①游标类量具一般读到游标分度值的整数倍。 如游标卡尺、分光计方位角的游标读数盘、椭圆偏振测量仪上的角度读数游标盘、水银大气压力计的读数标尺等。
②数显仪表及有十进制步进式标度盘的仪表,一般直接读取仪表的示值。 如电阻箱、电桥、电位差计等。
③指针式仪表一般要估读到最小分度值的1/10 ～1/4,或使估读间隔不大于仪器误差限的1/5 ～1/3。 由于人眼分辨能力的限制,一般很难估读到1/10 分度以下。
④对于一般可估读到最小分度值以下的计量器具,当最小分度不小于1 mm 时,通常要估读到1/10 分度。 如螺旋测微器和测量显微镜鼓轮的读数,都要估读到1/10 分度;少数情况下也可估读到1/5 或1/2 分度。 例如光具座上标尺的坐标读数可以估读到毫米分度的1/2 或1/5。
(2)运算过程中的数和中间运算结果的有效位数
在物理实验教学中,对参与运算的数以及中间运算结果都可以不作修约(或适当多取几位),只在最后结果表示前作修约,以避免修约过早带来过大的附加误差。
(3)测量结果最终表达式中的有效位数
实验测量结果的最终表达式包括测量的标准不确定度u、被测量的量值x 以及物理量的单位。
①不确定度的有效位数。
对于独立被测量的不确定度,规定只取1 ～2 位有效位数。 实验教学中约定:修约前首位数字较小时(如1、2 等)一般取两位,首位大于3 时通常取1 位;用百分数表示的相对不确定度也只取1 ～2 位。 另外,不确定度的计算,原则上“宁大勿小”,所以修约时通常“只进不舍”。
②被测量量值的有效位数。
最终测量结果的表达式X=x±ux 中,量值x 与不确定度ux 的末位数字一般要对齐。
测量结果为:R=(100.004 3±0.001 3) Ω。
有效位数的确定,既要能充分反映测量方法或数学方法本身的精密度,又要避免所取位数过多而做无用功或造成误解,因此,数值修约是数据处理的必要环节。 物理实验中要求“抓两头,放中间”,所谓“抓两头”,就是要重视原始数据读取和最后结果表示这一前一后两个环节;所谓“放中间”,就是中间运算过程中不要无根据地随意减少数据的位数,要适当多取几位,以避免过早舍入造成误差的亏损和累积效应。