2.7 霍尔传感器测量材料的杨氏模量
杨氏模量是描述固体材料在线度方向受力后抵抗形变能力的重要物理量。 它与材料自身性质有关,与材料的几何形状和所受到外力的大小无关,是工程设计中机械构件选材的重要参数和依据。 测量杨氏模量的常用方法有拉伸法、弯曲法、振动法和内耗法等,本实验采用梁弯曲法测量金属的杨氏模量。 实验中选用霍尔位置传感器实现对微小位移量的测量。
【实验目的】
①熟悉霍尔位置传感器的特性,掌握微小位移非电量电测新方法。
②学会用梁弯曲法测定金属的杨氏模量。
③掌握用逐差法处理数据。
【预习思考题】
①什么是霍尔效应?
②杨氏模量的定义是什么?
③梁弯曲法测量杨氏模量的计算式及意义是什么?
【实验原理】
1.霍尔效应
霍尔元件放在磁感强度为B 的磁场中,在垂直于磁场方向通有电流I,则与这二者垂直的方向上将产生霍尔电压UH:
![]()
式(2.33)中KH 为霍尔灵敏度。 如果保持霍尔元件中的电流I 不变,而使其在一个均匀梯度的磁场中移动时,则输出的霍尔电压变化量为

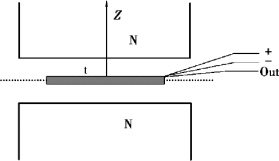
图2.19 霍尔效应示意图
式(2.34)中ΔZ 为位移量,由上式可知,若dB/dZ为常数,则ΔUH 与ΔZ 成正比。
为获得均匀梯度的磁场,可以用两块相同的磁铁N极与N 极相对,两磁铁之间留一等间距空位,如图2.19所示。 将霍尔元件平行于磁铁放在该空位的中轴上。空位大小要根据测量范围和测量灵敏度要求而定,空位越小,磁场梯度就越大,灵敏度就越高。 磁铁截面要远大于霍尔元件,以尽可能减小边缘效应的影响,提高测量精确度。
若磁铁间的空位中心截面处的磁感应强度为零,霍尔元件处于该处时,输出的霍尔电压就应该为零。 当霍尔元件偏离中心沿Z 轴发生位移时,由于磁感应强度不再为零,霍尔元件也就产生相应的电势差输出,其大小可以用数字电压表显示。 由此可以将霍尔电压为零时元件所处的位置作为位移参考零点。
霍尔电压与位移量之间存在一一对应关系,当位移量较小(<2 mm)时,这一对应关系具有良好的线性。
2.杨氏模量Y 的计算公式

![]()
式(2.35)中Y 称为杨氏模量,其数值决定于材料本身的性质,杨氏模量的大小反映了材料抵抗形变的能力。
将厚为a、宽为b 的金属板放在相距为d 的二刀口上,在金属片上二刀口的中点处挂上质量为m 的砝码,板被压弯,挂砝码处下降ΔZ。 在待测样品发生微小弯曲时,梁中存在一个中性面m,面上部分发生压缩,面下部分发生拉伸,所以整体来说,可以理解为待测样品发生应变,可用杨氏模量来描写材料的性质,杨氏模量的大小为

【实验仪器】
1.杨氏模量实验装置
霍尔位置传感器法杨氏模量测定仪(图2. 20);读数显微镜(放大倍数20 倍,分度值0.005 mm,测量范围0 ~6 mm);螺旋测微器;游标卡尺;米尺;砝码(10.0 g、20.0 g 两种)等。
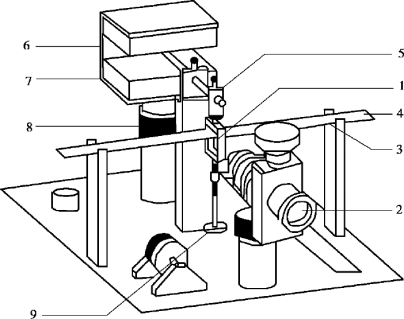
图2.20 杨氏模量实验装置
1—铜刀口上的基线;2—读数显微镜;3—刀口;4—横梁;
5—铜杠杆(顶端装有霍尔传感器);6—磁铁盒;7—磁铁(N 极相对位置);8—三维调节架;9—砝码。
2.杨氏模量测定仪
杨氏模量测定仪面板图如图2.21 所示。

图2.21 杨氏模量测定仪面板图
三位半数字面板表(0 ~199.9 mV,0.1 mV 和0 ~1.999 V,1 mV 两种量程)。
【实验内容及步骤】
1.测量黄铜样品的杨氏模量
(1)测量梁的弯曲微小位移ΔZi
①以水准器为参照,调节底座螺丝使装置水平。
②调节三维架上下前后的螺丝,使霍尔位置传感器探测元件处于磁铁中间。
③磁铁盒上可上下调节螺丝使磁铁上下移动,当毫伏表读数值很小时,停止调节,最后调节调零电位器使毫伏表读数为零。
④调节读数显微镜。 调节目镜,使标尺和准线(两条小横线)清晰。 调节显微镜的高度,使其对准刀口架上的基线。 然后移动读数显微镜前后距离,使待测目标(刀口架上的标记刻线)成像清晰,调整后紧固螺丝。 微调显微镜的支柱螺杆,使待测标记成像于视场的中央偏下方部位。 转动显微镜的读数鼓轮,从目镜中可看到准线上下移动,使准线与标记刻线完全重合,记下读数作为测量的初始位置值Z0。
⑤逐次增加砝码mi(每次增加10 g 砝码),读出每次准线与标记刻线重合时读数显微镜的读数Zi(金属片的弯曲位移ΔZi =Zi -Z0)及相应的数字电压表读数值Ui。 以便计算杨氏模量和霍尔位置传感器进行定标。 在整个测量过程中都要注意避免读数显微镜的空程误差,即只允许准线向一个方向移动。
⑥用逐差法处理数据,计算梁的弯曲微小位移ΔZi。
(2)测量其他物理量
①测量横梁两刀口间的长度d(用30 cm 的直钢尺)。
②测量不同位置横梁宽度b(用游标卡尺)。
③测量横梁厚度a(用螺旋测微器)。(https://www.daowen.com)
2.用霍尔位置传感器测量可锻铸铁的杨氏模量(选做)
①逐次增加砝码mi,读出数字电压表的数值。 由霍尔位置传感器的灵敏度,计算出下降的距离ΔZi。
②测量不同位置的金属板宽度b 和金属板厚度a。 用逐差法按式(2.36)计算可锻铸铁的杨氏模量。
3.注意事项
①实验开始前,必须检查横梁是否有弯曲,如有应矫正。
②梁的厚度必须测准确。 用千分尺测量待测样品的厚度时,必须取不同位置多点测量取平均值。 测量黄铜样品时,因黄铜比钢软,旋紧千分尺时,当将要与金属接触时,必须用微调轮。 当听到“嗒嗒嗒”三声时,停止旋转。 用力要适当,不宜过猛。
③霍尔位置传感器定标前,应先将霍尔位置传感器调整到零输出位置,这时可调节永磁铁盒下的升降杆上的旋钮,达到零输出的目的,另外应使霍尔位置传感器的探头处于两块磁铁的正中间(磁铁上有十字标线)稍偏下的位置,这样测量数据更可靠一些。
④测量中注意避免读数显微镜的空程误差。
【数据处理与分析】
霍尔位置传感器实验数据表见表2.21。
表2.21 霍尔位置传感器实验数据表

①用逐差法算出样品在m=40.00 g 的作用下产生的位移量:
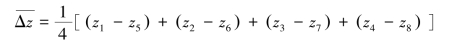
②按式(2. 36)进行计算,计算黄铜材料的杨氏模量,并求出霍尔位置传感器的灵敏度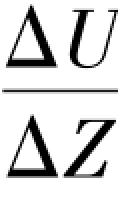 。
。
③把测量结果与公认值(黄铜材料的杨氏模量公认值E=10.55×1010N/m2)进行比较。
【课后讨论】
①弯曲法测杨氏模量实验,主要测量误差有哪些? 请估算各因素的不确定度。
②用霍尔位置传感器法测位移有什么优点?
【附】
实验数据处理举例(逐差法)
1.霍尔位置传感器的定标
在进行测量之前,要求符合上述安装要求,并且检查金属板的水平、刀口的垂直、挂砝码的刀口处于梁中间,一切正常后加砝码,使梁产生位移ΔZ;精确测量传感器信号输出端的数值与固定砝码架的位置Z 的关系,也就是用读数显微镜对传感器输出量进行定标,测量数据间表2.22 所示。
表2.22 霍尔位置传感器实验数据表

2.杨氏模量的计算
用直尺量得横梁的长度d=22.68 cm,游标卡尺测其宽度b=2.290 cm,千分尺测其厚度a=0.950 mm。
用逐差法算出样品在m=40.00 g 的作用下产生的位移量Δz。
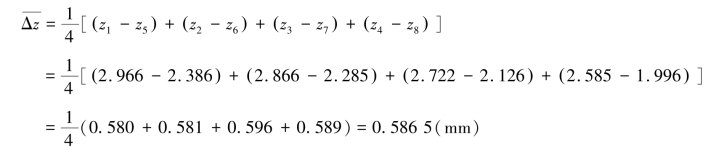
代入式(2.36)得黄铜的杨氏模量
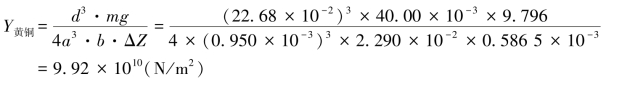
霍尔位置传感器的灵敏度为
![]()
与公认值比较,得百分误差
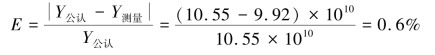
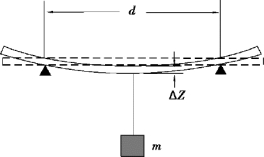
图2.22 梁弯曲法
3.梁弯曲法测杨氏模量计算公式推导
将厚为a、宽为b 的金属板放在相距为d 的二刀口上,如图2.22 所示,在金属板上二刀口的中点处挂上质量为m 的砝码,板被压弯,设挂砝码处下降ΔZ。
如图2.23(a)所示,在相距dx 的O1O2 二点上的横断面,在金属板弯曲前互相平行,弯曲后则成一小角。 显然,在金属板弯曲后,其下半部呈现拉伸状态,上半部为压缩状态,而在金属板的中间的一薄层虽弯曲但长度不变,称为中间层。 假设与中间层相距为y、厚dy、形变前长为dx 的一段,弯曲后伸长了ydφ,受到的拉力为dF,那么整个横断面的转矩应是
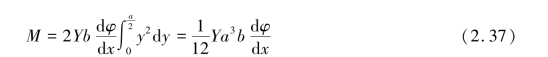

![]()
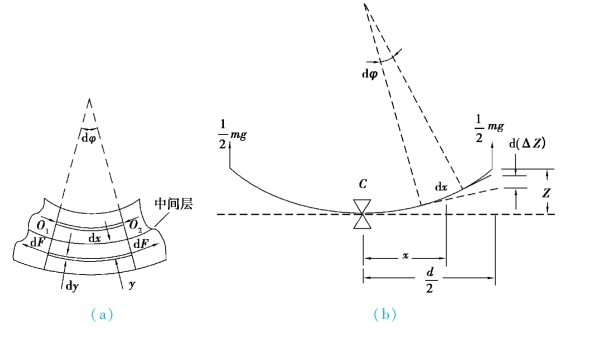
图2.23 梁弯曲法公式推导
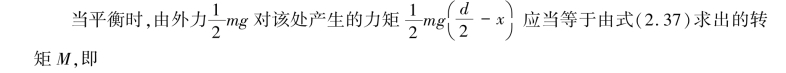
![]()
由此式求出dφ 代入式(2.38)中并积分,可求出
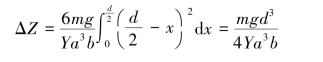
则有

