1.5 实验数据处理的基本方法
实验数据处理是指对所有实验数据进行整理、分析、计算,做成图、表等,或将所有数据归纳成一定表达式,揭示物理量之间的变化关系,乃至得到一个客观、合理的实验结果的全过程。而采用的数据处理的方法是否正确、恰当,对最后获得准确可靠的实验结论至关重要。
常用的数据处理方法有列表法、作图法、图解法、逐差法、回归分析等,在实验数据处理的过程中可能会用到一种或多种方法,下面分别予以介绍。
1.列表法
列表法指在记录和处理数据时,将数据记录、整理、排列成表格形式的一种方法。 它是实验数据处理的基础,应当熟练掌握。
(1)列表的作用
①可以清楚、简明地表示相关物理量之间的对应关系,揭示相关数据之间的实验规律,从而求出经验公式。
②便于减少和避免错误,便于发现问题数据,便于随时检查数据并发现错误。
③提高记录和处理数据的工作效率。
(2)列表的要求
①所列表格清晰明了,使读表人能较容易地看出相关物理量之间的关系,便于处理数据。
②表格中应包含一些基本的信息,比如物理量的名称、符号、单位等。 注意:在表格中物理单位不要重复写入。
③表格中的数据应正确反映测量值的有效数字。 列入表中的主要数据是原始数据,处理过程中一些重要的中间结果也需要列入表格。
④提供表格相关的说明和参数。 包括表格的名称、主要测量仪器规格(型号、量程及准确度等级等)、相关测量环境参数和其他需要引用的物理常数等。
(3)列表法举例(表1.3)
表1.3 小球直径测量数据表(千分尺:0 ~25 mm,0.004 mm)

说明:
①标题栏中给出了测量仪器的相关参数。
②表内物理量的名称、符号和单位正确。
③表格内填写了完整的原始数据,数据中有些重要计算也应直接写入。
④通过νi 所在行数据可以看出,在第9 次测量中ν9 =- 0.108,很可能第9 次测量值有问题,按照格拉布斯准则计算后该数据应剔除。
⑤列表之后要对数据继续进行相应的处理,并最终得到测量结果,不能简单地认为此时实验已经结束。
2.作图法和图解法
作图法就是将已知量和测量量的所有数据按照一定的对应关系用图线表示出来的一种常用的数据处理方法。 图解法就是依据数据所给出的图线,实验者可以研究物理量之间的变化关系,并找出其中的规律,确定对应量的函数关系并求出经验公式的方法。
(1)作图的基本原则
①选择合适的坐标纸。 常用坐标纸有直角坐标纸(毫米方格纸)、极坐标纸、对数坐标纸、双对数坐标纸等。 应根据具体的实际情况选择合适的坐标纸。
②坐标轴和标尺的选择。 一般用横轴代表自变量,用纵轴代表因变量。 将要作图的物理量的数值归纳、整理并填入表格,在选定的坐标纸上标明标度、方向、代表的物理量和单位等。要合理选择两坐标轴的比例和坐标原点,便于所得图线均匀地填充至整个图纸。
注意:将分度值均匀地标记于坐标轴上,且在分度时应以容易确定且便于计算的数值进行标记。 如选择“1、2、5”,不选择“3、5、7”等。
③标点。 根据原始测量数据用尖锐的铅笔将对应的数据用“+、×、●、◆”等符号标记在坐标纸上,然后根据这些数据绘制出平滑的曲线(校准曲线除外)。 连线时需用直尺或曲线板。在实验范围以内画直线,实验范围以外画虚线。
④写明图线的名称。 一般在图的下方标注图线的名称,图名中通常把纵轴所代表的物理量写在前面。 同时在图中注明必要的实验条件。
(2)直线图解法
如果数据中自变量,因变量x、y 属线性关系,则可用y=a+bx 表示。 只要求出斜率和截距,即可得出完整的线性方程。 可按下列步骤进行:
①选点。 通常在所作的图线上选取两个点,所选点一般不用实验点,并用与实验点不同的符号标记,此两点应尽量在直线的两端。 如记为A(x1,y1)和B(x2,y2),并用“+”表示实验点,用“⊙”表示选点。
②求斜率。 根据直线方程y=a+bx,将两点坐标代入,可解出图线的斜率:

③求与y 轴的截距:

④求与x 轴的截距:

(3)曲线改直法
直线绘制简单,而且直线方程的两个参数(截距和斜率)也较容易计算。 在已知函数关系的情况下,作两变量之间的关系图线时,可将非线性函数曲线转换为线性函数曲线。 常用的曲线改直线的方法有以下几种。
①y=axb,a、b 为常数。 则ln y=ln a +b ln x,ln y—ln x 图是一条直线,斜率为b,截距为ln a。
②y=ae-bx,a、b 为常数。 则ln y = ln a - bx, ln y—x 图是一条直线,斜率为-b,截距为ln a。
③y=abx,a、b 为常数。 则ln y=ln a +x ln b,ln y—x 图是一条直线,斜率为ln b,截距为ln a。
![]()
⑤y2=2ax,a 为常数。 则y2—x 图是一条直线,斜率为2a。
⑥y2=a2-x2,a 为常数。 则y2—x2 图是一条直线,斜率为-1,截距为a2。
下面举例说明:
例如,已知某电容器放电过程中的物理量x 和y 按下列规律变化
![]()
式中,A 和B 是未知常数,需要用图解法处理数据。 如果用半对数坐标纸作图,以y 为纵轴(对数坐标),则y=Ae-Bx 变为lg y=-B(lg e)x +lg A,由直线斜率可求B,截距可求A;如果不用半对数坐标纸,而用直角坐标纸则可先计算lg y 后再作lg y-x 图,也可在直角坐标纸上得到直线。

3.逐差法
逐差法是物理实验中一种常用的数据处理方法。 当自变量是等间距变化,因变量按测量顺序存在多项式函数关系时,常选用逐差法来处理数据。
逐差是将测量得到的实验数据“逐项相减”,或者“按因变量的大小顺序排列后平分为前、后(或高、低)两组实行对应项相减”。 “逐项相减”可以在测量中随时进行,以判断测量是否正确。 而当自变量与因变量呈线性关系时,对自变量等间距变化的多次测量,则必须按后一种方法进行数据处理。
例如,用霍尔位置传感器法测量金属杨氏模量实验,测得该金属横梁中心位置Zi(mm) 读数与所加挂砝码质量mi(g) 的关系,实验数据见表1.4。 求每次载荷50 g 砝码,金属横梁中心位置的微小改变量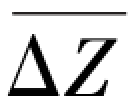 。
。
表1.4 用霍尔位置传感器法测量金属杨氏模量实验数据

解①:用“逐项相减”的方法来进行计算。
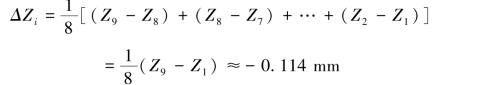
很显然可以看出中间值全无用,只有第一次和最后一次测量值起作用。 这样和单次测量没有什么区别。
解②:用“前、后两组对应项相减”的方法来进行计算,见表1.5。
表1.5 用逐差法处理微小位移量表格1
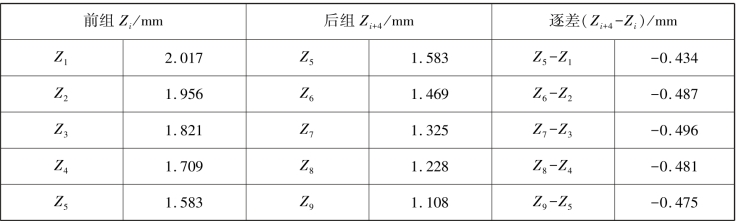
求差平均:(https://www.daowen.com)
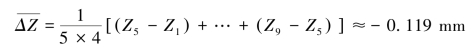
解③:用“高、低两组对应项相减”的方法来进行计算,见表1.6。
表1.6 用逐差法处理微小位移量表格2
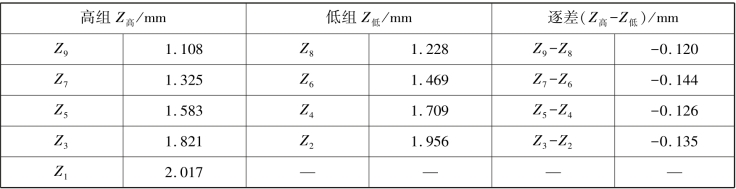
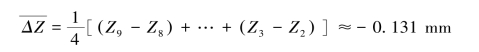
不难看出,解②和解③中使用的数据量都比解①要多,这样可以充分利用数据,体现多次测量的优点,减小测量误差。
4.回归分析
无论是图解法还是逐差法都有一定的局限性,因为它们不是建立在严格的统计理论基础上的数据处理方法。 比如在图解法中,用同样一组数据在作图纸上作图,不同的人可以画出不同的曲线,自然他们得出的测量结果也就不同。 又如在上述逐差法的举例中,解②和解③虽然都用了逐差法,但是测量结果却不同。 而回归分析则是利用概率统计的基础知识进行分析、讨论、处理多个变量之间相互关系的一种数据处理方法。
(1)回归分析的本质
回归分析是处理多个变量之间相关关系的一种数学方法。 相关关系和函数关系不同,变量之间没有确定性关系。 例如,材料性能与温度之间的关系就是一种相关关系,而没有确定关系,原因是材料性能往往由多种因素共同决定,如组成、结构、工艺参数等。
从变量之间的依存关系来看,回归分析包括以下几种。
①一元线性回归分析:一个变量的变化仅仅取决于另一个变量的变化,两个变量之间呈线性关系。
②一元非线性回归分析:一个变量的变化仅仅取决于另一个变量的变化,两个变量之间呈非线性关系。
③二元或多元回归分析:一个变量的变化取决于两个或两个以上变量的变化,变量之间呈线性或非线性关系。
在实验中我们主要学习并使用一元线性回归分析进行数据的处理。
(2)一元线性回归分析
回归分析的任务之一就是确定具有相关关系的变量之间的经验关系式,以便由一个(或几个)变量的数值估计出另一个变量的数值。 一元线性回归所要考虑的仅仅是两个变量之间的关系,假如要分析一对变量X 和Y 的相关关系,可以通过来自X 和Y 这两个总体的一组数据(xi,yi)(i=1,2,…,n)来确定X 和Y 之间的经验公式,即
![]()
上式是Y 关于X 的回归方程,其中y 是Y 的估计值。
例如,某种合成材料的强度与其拉伸倍数有关,表1.7 是24 个材料试样的强度与相应的拉伸倍数的实测记录,试建立这两个变量之间的关系。
表1.7 某材料的拉伸强度与拉伸倍数
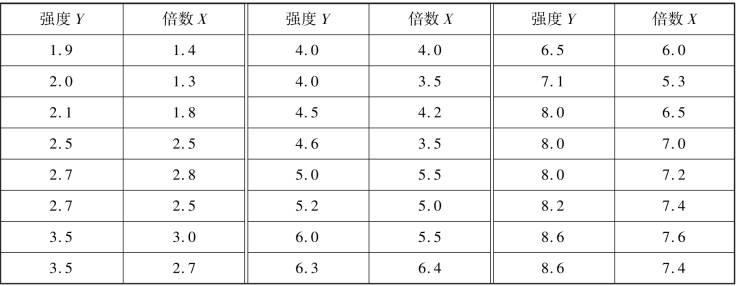
根据解析几何知识,在平面上选取一个直角坐标系,把这24 对数据对应的点画在坐标系中,得到如图1.2 所示的散点图。
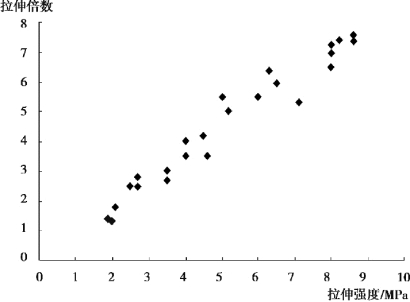
图1.2 拉伸强度与拉伸倍数散点图
从图1.2 可以看出,这些点大致分布在某一条直线的两侧。 也就是说,拉伸倍数与拉伸强度之间大体上呈线性关系。 如果配置一条直线,则可写成
![]()
这里,在y 上方加记号“^”是因为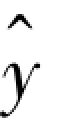 是由经验公式得到的Y 的估计量,它区别于Y 的实际值y。
是由经验公式得到的Y 的估计量,它区别于Y 的实际值y。
式(1.25)便是所要求的Y 和X 的定量关系式,称为回归方程。 要求出回归方程,就必须确定式中的a 和b。 下面用最小二乘法原理来求a 和b。实际测量值yi 和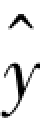 的差异:
的差异:
![]()
右侧平方得到:
![]()
将所有点的差异平方加起来得到偏差(离差)平方和:
![]()
这个量反映了直线与各点之间总的偏差程度,它是随不同直线变化的,或者说是随不同的a 与b 而变化的,所以它是a、b 的二元函数,记为Q(a,b),于是:


由于Q(a,b)是n 个数值的平方和,所以“使Q(a,b)最小”的原则称为最小二乘法原则(也称平方和最小原则)。 按照以上原则,用微分求极值的方法,求解二元一次联立方程:
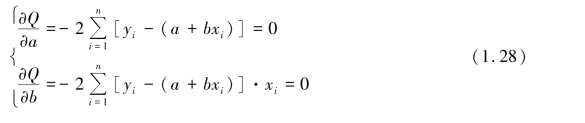
或写成
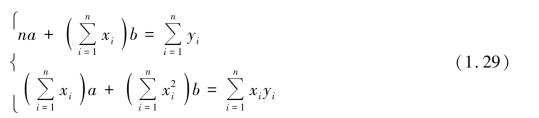
不难求解得

其中
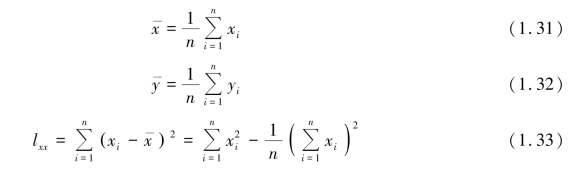
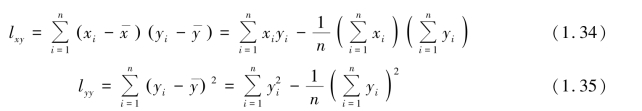
将由式(1.30)计算得到的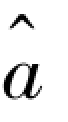 和
和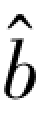 的值代入式(1.25),得到所求的线性方程:
的值代入式(1.25),得到所求的线性方程:
![]()
这个方程叫做Y 关于X 的线性方程,其中,b^ 被称为回归系数,对应的直线叫做回归直线。
(3)线性拟合的有效性分析
实验测量数据y1,y2,…,yn 的偏差(离差)平方和定义为
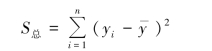
偏差(离差)平方和S总反映了观测值yi 总的分散程度,对S总进行分解,得
![]()
![]()
![]()
式中S回称为回归平方和,它反映了回归值yi 的分散程度,这种分散是由Y 与X 之间的线性相关关系引起的。
S余称为残差平方和,它反映了观测值yi 偏离回归直线的程度,这种偏离是由观察误差等随机因素引起的。
引入统计量:

如果Y 与X 之间的线性相关关系显著,则S回的值较大,S余的值较小。 因而F 的值也较大;反之,如果Y 与X 之间的线性相关关系不显著,则F 的值较小。
我们也可以根据相关系数R 的大小来判断是否线性相关。
对于相关系数R:
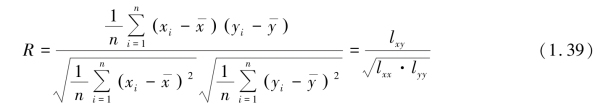
当R 的值越接近1,Y 与X 之间的线性相关关系越显著。 当R>0 时,称Y 与X 正相关;当R<0 时,称Y 与X 负相关;当R 的绝对值接近0 时,可以认为Y 与X 之间不存在线性相关关系。
