3.1 等厚干涉及应用
光的干涉现象为光的波动性提供了有力的实验证明。 生活中能见到许多与干涉有关的现象,比如彩色的肥皂泡,雨后路上的彩色油膜等,都与光的干涉相关,都能够用光的波动性来说明其中的原理。 光的干涉广泛应用于科学研究、工业生产和检测技术中,如用于测量光波波长,精确测量微小物体的长度、厚度和角度,检测加工工件表面的光洁度和平整度及机械元件的内应力分布等。
要使两束光线发生干涉现象,那么这两束光必须是相干光,即频率相同、振动方向相同、相位差恒定。 实验中获得相干光的方法一般有两种:分波阵面法和分振幅法。 此次要进行的等厚干涉实验属于分振幅法产生的干涉现象。
【实验目的】
①通过观察干涉图样的特点,加深对等厚干涉的理解。
②学会测量平凸透镜曲率半径的方法。
③学会读数显微镜的使用方法。
【实验原理】
1.等厚干涉
当一束单色光入射到透明薄膜上时,薄膜上下表面依次反射产生两束相干光。 如果这两束反射光相遇时的光程差仅取决于薄膜厚度,则同一级干涉条纹对应的薄膜厚度相等,这就是所谓的等厚干涉。 牛顿环和劈尖干涉都是典型的等厚干涉。
如图3.1 所示,玻璃板A 和玻璃板B 二者叠放起来,中间加有一层空气(即形成了空气劈尖)。 设光线1 垂直入射到厚度为d 的空气薄膜上。 入射光线在A 板下表面和B 板上表面分别产生反射光线2 和2′,二者在A 板上方相遇,由于两束光线都是由光线1 分出来的(分振幅法),故频率相同、相位差恒定(与该处空气厚度d 有关)、振动方向相同,因而会产生干涉。 我们现在考虑光线2 和2′的光程差与空气薄膜厚度的关系。 显然光线2′比光线2 多传播了一段距离2d。 此外,由于反射光线2′是由光密介质(玻璃)向光疏介质(空气)反射,会产生半波损失。 故总的光程差还应加上半个波长λ/2,即
![]()
根据干涉条件,当光程差为波长的整数倍时相互加强,出现亮纹;为半波长的奇数倍时互相减弱,出现暗纹。
因此有
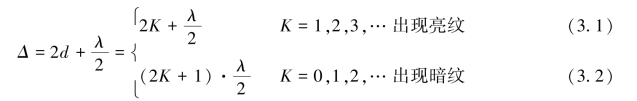
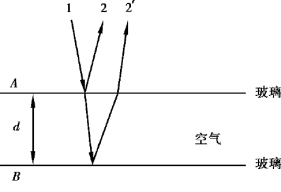
图3.1 等厚干涉
光程差Δ 取决于产生反射光的薄膜厚度。 同一条干涉条纹所对应的空气厚度相同,故称为等厚干涉。
2.牛顿环
将一块圆形平面凸透镜放置在一块圆形平板玻璃上,两者之间存在一个空气间隙,如图3.2 中所示。 将平凸透镜与平板玻璃的接触点记作O 点,空气间隙的厚度从O 点到边缘逐渐增加。 若有一束单色光垂直入射到平凸透镜上,该光线在平凸透镜下表面和平板玻璃上表面的反射光会产生干涉,形成明暗相间、中心疏边缘密的同心圆环状干涉条纹,我们称这种干涉图样为牛顿环。
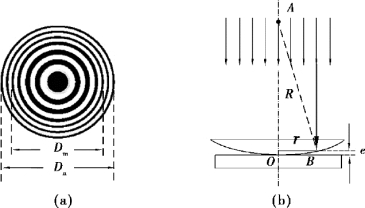
图3.2 牛顿环图像与牛顿环仪器
将平凸透镜的曲率半径记作R,环纹半径记作r,图中B 点处的空气厚度记作e,由图中三角形AOB 可以得到
![]()
由于空气层e 是极小量,故式中e2 可略去,得
![]()
将式(3.4)代入式(3.1)和式(3.2),可得反射光中明环与暗环的半径分别为
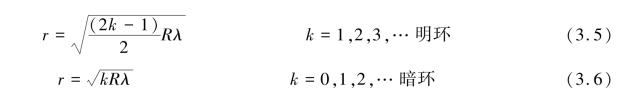
第m 级和第n 级暗环的半径为
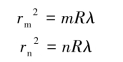
两式相减得平凸透镜的曲率半径计算公式
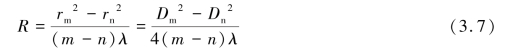
注:式(3.7)中,因第m 级和第n 级的序数差与第m 级和第n 级的级数差相等,所以在实际测量中,不用考虑观察到的牛顿环级数到底是多少。
3.劈尖干涉(https://www.daowen.com)
在劈尖架上两个光学平玻璃板中间的一端插入一薄片(或细丝),则在两玻璃板间形成一空气劈尖。 当一束平行单色光垂直照射时,则被劈尖薄膜上下两表面反射的两束光进行相干叠加,形成干涉条纹。 其光程差为

产生的干涉条纹是一簇与两玻璃板交接线平行且间隔相等的平行条纹,如图3.3 所示。同样根据牛顿环的明暗纹条件有
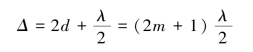
m=0,1,2,3…时,为干涉暗纹
![]()

![]()
用α 表示劈尖形空气隙的夹角、s 表示相邻两暗纹间的距离、L 表示劈间的长度,则有
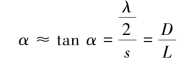
则薄片厚度为

由式(3.9)可见,如果求出空气劈尖上总的暗条纹数,或测出劈尖的L 和相邻暗纹间的距离s,都可以由已知光源的波长λ 测定薄片厚度(或细丝直径)D。
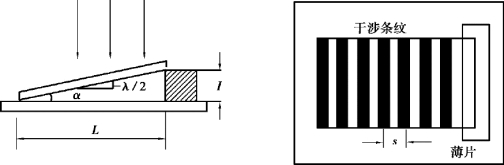
图3.3 劈尖干涉测厚度示意图
【实验仪器】
牛顿环仪、劈尖、钠光灯、读数显微镜等。
【实验内容及步骤】
牛顿环测平凸透镜的曲率半径的步骤如下:
①接通钠光灯电源使灯管预热,调节牛顿环仪边框上的三个螺旋,使在牛顿环仪中心出现一组同心干涉环。
②将牛顿环仪N 放在读数显微镜的平台上,调节45°反射镜G,如图3.4 所示。
③调节读数显微镜调焦手轮,直至在读数显微镜内能看到清晰的干涉条纹的像。 适当移动牛顿环位置,使干涉条纹的中央暗区在显微镜叉丝的正下方, 观察干涉条纹是否在读数显微镜的读数范围内,以便测量(注意:调焦过程中应该先将读数显微镜调下, 然后向上调焦,以免压坏牛顿环和劈尖)。
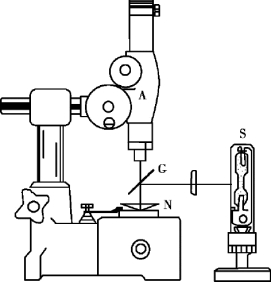
图3.4 读数显微镜测牛顿环装置
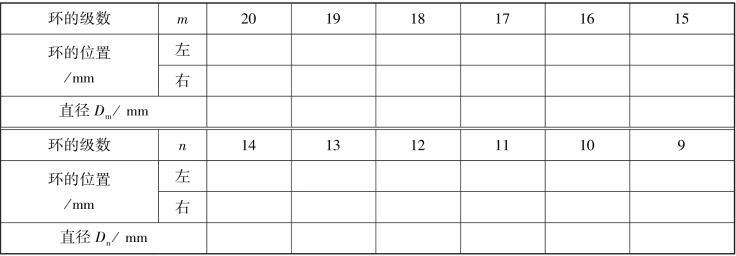
④转动读数鼓轮,观察十字准线从中央缓慢向左(或向右)移至23 环,然后反方向至第20环向右移动,当十字准线竖线与20 环中心相切时,记录读数显微镜上的位置读数,然后继续转动鼓轮,使竖线依次与19、18、17 等环中心相切,并记录读数于表3.1 中。
⑤继续按原方向转动读数鼓轮,越过干涉圆环中心,记录十字准线与右边第9 至20 环中心相切时的读数于表3.1 中。 注意整个测量过程中鼓轮不能倒转。
【数据处理与分析】
牛顿环测平凸透镜的曲率半径实验数据记录见表3.1。
表3.1 牛顿环测平凸透镜的曲率半径
【课后讨论】
钠光波长λ=589.3 nm;用逐差法计算出曲率半径。
