1.3　间接测得量的误差估算

1.3　间接测得量的误差估算

在物理实验中,除直接测量外,大部分实验都是经过间接测量获得最终结果。 间接测量是以直接测量为基础,按某种函数关系求出待测量。 由于各直接测量量有误差,这些误差必然影响间接测量量,这就是误差传递。 各直接测量量的误差与间接测量量的误差之间的关系式,称为误差传递公式。

1.误差传递的基本公式

设y =F(x1,x2,…,xm) ,其中x1,x2,…,xm 为m 个直接测量量,y 为间接测量量,将各直接测量量的算术平均值代入公式,即可求出间接测量量的最佳估计值。 即

当考虑各直接测量量的误差时,间接测量量也有误差,所以有

按泰勒公式展开式(1.11)并略去二次方及以上得

在计算偶然误差时,由于误差本身的正或负是不可知的,因此,上式中各误差项的系数必须取其绝对值,即

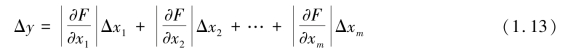
相对误差为

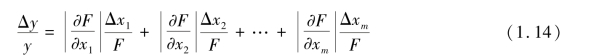
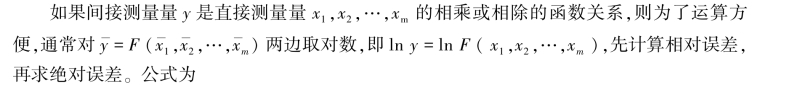
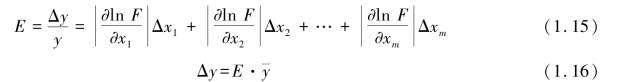
以上讨论没有考虑各误差项的实际符号,而总是从最不利的情况讨论,忽略了一些可以相互抵消的情况,因而估计出的误差将偏大。 根据上述公式,可推导出表1.1 所列的一些常用函数关系式的误差传递公式。

表1.1　常用函数关系式的误差传递公式

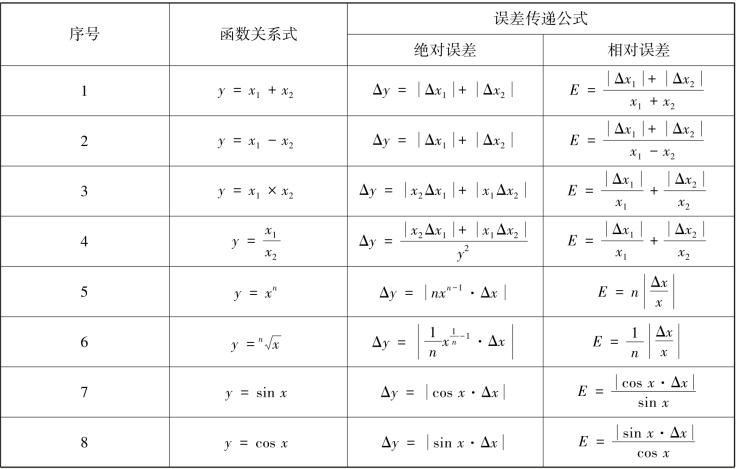
由表1.1 所列常用函数关系式的误差传递公式,可总结出如下规律:

①当间接测量量是几个直接测量量的和(或差)时,间接测量量的绝对误差等于各直接测量量的绝对误差之和。 在此情况下,先算绝对误差,后算相对误差较方便。

②当间接测量量是几个直接测量量的积(或商)时,间接测量量的相对误差等于各直接测量量的相对误差之和。 在此情况下,先算相对误差,后算绝对误差较方便。

2.标准误差的传递公式

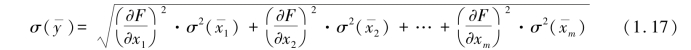
其相对误差为

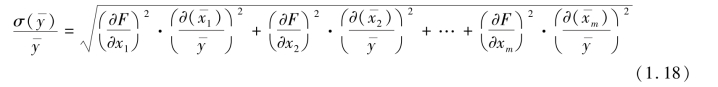
同样,当间接测量量是各直接测量量的积(或商)时,先求标准误差的相对误差较方便,其公式为

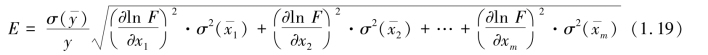
标准误差为

根据上面的公式,可以推导出表1.2 所列的一些常用函数的标准误差传递公式。

表1.2　一些常用函数的标准误差传递公式