3.5 薄凸透镜焦距的测量
透镜是用透明物质制成的表面为球面一部分的光学元件。 它是最常用的光学元件,是构成显微镜、望远镜等光学仪器的基础。 当透镜的厚度比透镜的焦距小很多时,我们就把它叫做薄透镜。 按形状分类,透镜可以分为凸透镜和凹透镜两类。 凸透镜又可以分为双凸透镜、平凸透镜和凹凸透镜。
焦距是表征透镜成像性质的重要参数。 学生学习透镜焦距的测量,不仅可以加深对几何光学中透镜成像规律的理解,而且有助于提高光路分析能力,掌握光学仪器的调节技术。
【实验目的】
①理解凸透镜成像的原理及规律。
②掌握凸透镜的测量原理,学会用多种方法测量其焦距。
【预习思考题】
①怎样用一个最简单的方法来区别凸透镜和凹透镜? (不许用手摸)
②实验中为什么要求物像间距要大于4 倍焦距?
【实验原理】
1.透镜成像的基本概念
主光轴:通过透镜两个折射曲面中心的直线。
光心:光线通过主光轴上不改变方向的某一点。
焦点:平行于主光轴的光线,在通过透镜后汇聚于主光轴上的点。
焦距:焦点到光心之间的距离。
物距:物体到透镜光心之间的距离。
像距:像到透镜光心之间的距离。
透镜成像公式:

以上两式中, f 为透镜焦距,u 为物距,ν 为像距。
2.物距-像距法(公式法)测透镜焦距
如图3.20 所示,分别测得物距与像距,利用式(3.36)可计算出透镜焦距。
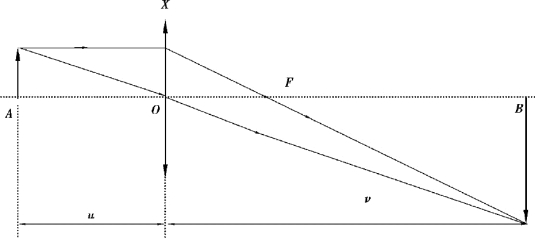
图3.20 物距-像距法测透镜焦距
3.共轭法(两次成像法、贝塞尔法)测透镜焦距
在用物距像距法测量的时候,由于光心的位置不能够准确确定,导致测量出的物距和像距出现误差,消除这一系统误差的方法之一就是共轭法。
如图3.21 所示,如果物屏与像屏的相对位置D 保持不变,而且D>4f,那么在物屏到像屏之间移动透镜,可以得到两次成像。 由透镜的成像公式可以写出这两次成像的公式:

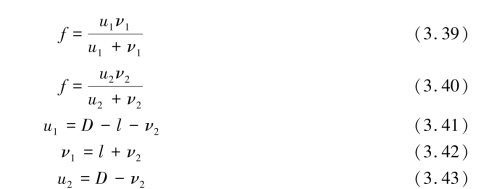
将式(3.41)和式(3.42)代入式(3.39)可得
![]()
将式(3.43)代入式(3.40)可得:

将式(3.44)与式(3.45)联立可得
![]()
将式(3.46)代入式(3.45)可得

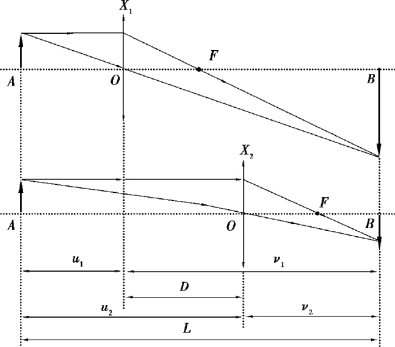
图3.21 共轭法测凸透镜焦距
4.自准法测凸透镜焦距(https://www.daowen.com)
将物屏置于透镜的焦平面上,发出的光经过凸透镜后成为平行光,在透镜后放置一面平面镜,使其与主光轴垂直。 平行光射向平面镜并沿原路反射回来,仍会聚在焦平面上,形成一个倒立等大的像。 此时物屏至透镜光心的距离就是焦距,如图3.22 所示。
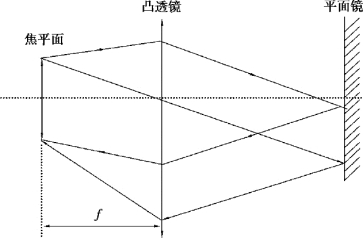
图3.22 自准法测凸透镜焦距
【实验仪器】
薄凸透镜、点光源、物屏、像屏、平面镜、万能光具座等,如图3.23 所示装置图。

图3.23 薄凸透镜焦距测量装置图
【实验内容及步骤】
1.调节光具座上各元件使其共轴等高
①先将点光源、物屏、薄凸透镜、像屏靠拢在一起,目测调节高低、角度,使得它们的中心大致在一条和导轨水平的直线上,并且使各元件平面平行。
②保持点光源和像屏位置不变,调节物屏与薄凸透镜的相对高度,使得移动薄凸透镜时,像屏上的像由大到小围绕一个中心变化。 可以归纳总结为“大像追小像,中心相重合”。
2.利用物距-像距法测量凸透镜焦距
①确定物屏与像屏间的距离大于4 倍焦距,并保持不变。 记录物屏与像屏间的距离。
②当像屏上出现一个清晰的像时,记录此时薄凸透镜的位置。 重复6 次,记录于表3.9 中。
3.用共轭法测量凸透镜焦距
①确定物屏与像屏间的距离大于4 倍焦距,并保持不变。 记录物屏与像屏间的距离。
②移动透镜的位置可以在像屏上看到两次成像,分别记录成大像和小像时,透镜的位置。
③重复①、②,记录于表3.10 中。
注意:在寻找放大的实像时,应将点光源靠近物屏。 在寻找缩小的实像时,应将点光源远离物屏。
4.用自准法测量凸透镜的焦距(选做)
①元件从左至右依次安放点光源、物屏、薄凸透镜、平面镜。 保持光源和物屏位置不变。记录物屏位置。
②调节透镜到物屏间的距离和高低,并且始终保持平面镜紧靠薄凸透镜。 直到在物屏上出现等大倒立聚焦清晰的像。 此时物屏到透镜间的距离就等于薄凸透镜的焦距。 记录薄凸透镜位置。 重复6 次,记录于表3.11 中。
【数据处理与分析】
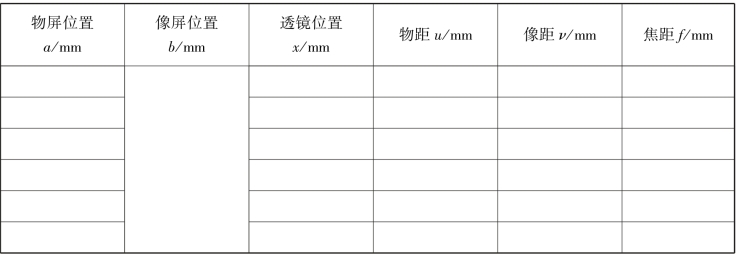
1.物距-像距法测凸透镜焦距
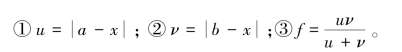
表3.9 物距-像距法测凸透镜焦距
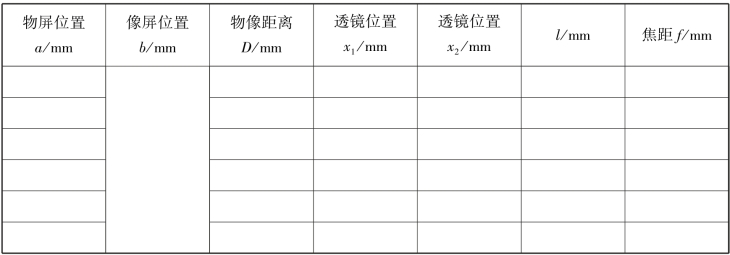
2.共轭法测凸透镜焦距
![]()
表3.10 共轭法测凸透镜焦距
3.自准法测凸透镜焦距
f = a - b。
表3.11 自准法测凸透镜焦距(选做)

【课后讨论】
①利用所学知识,举例说明凹透镜焦距的测量方法。
②本实验中如果没有共轴等高,则对实验结果有什么影响?
