2.2.2 风险报酬模型
1.风险衡量
由于风险具有普遍性和广泛性,那么正确地衡量风险就十分重要。既然风险是可能值对期望值的偏离,因此利用概率分布、期望值和标准差来计算与衡量风险的大小是一种最常用的方法。
(1)概率
在经济活动中,某一事件在相同的条件下可能发生也可能不发生,这类事件称为随机事件。概率就是用来表示随机事件发生可能性大小的数值。通常,把必然发生的事件的概率定为1,把不可能发生的事件的概率定为0,而一般随机事件的发生概率是介于0与1之间的一个数。概率越大就表示该事件发生的可能性越大。
【例2-16】 ABC公司有两个投资机会,A 投资机会是一个高科技项目,该领域竞争很激烈,如果经济发展迅速并且该项目搞得好,取得较大市场占有率,利润会很高;否则,利润会很低甚至亏本。B项目是一个老产品并且是必需品,销售前景可以准确预测出来。假设未来的经济情况只有三种:繁荣、正常、衰退,有关的概率分布和预期报酬率见表2-1。
表2-1 ABC公司未来经济情况表
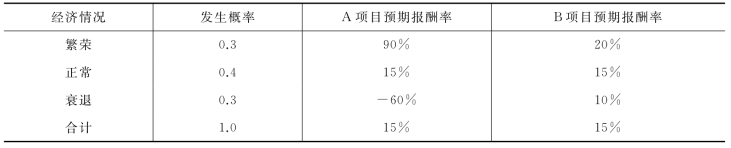
在这里,概率表示每一种经济情况出现的可能性,同时也就是各种不同预期报酬率出现的可能性。例如,未来经济情况出现繁荣的可能性有0.3。假如这种情况真的出现,A项目可获得高达90%的报酬率。这也就是说,采纳A项目获利90%的可能性是0.3。从上表中可见,所有的概率均在0和1之间,且概率之和为1。
如果我们将ABC公司年收益的各种可能结果及各种结果相应的概率按一定规则排列出来,构成分布图,则称之为概率分布。概率分布一般用坐标图来表示,横坐标表示某一事件的结果,纵坐标表示每一结果相应的概率。概率分布有两种类型:一是离散型概率分布,其特点是各种可能结果只有有限个值,概率分布在各个特定点上,是不连续图像;二是连续型概率分布,其特点是各种可能结果有无数个值,概率分布在连续图像上的两点之间的区间上。例2-16的概率分布就属于离散型分布,它有3个值,如图2-6所示。
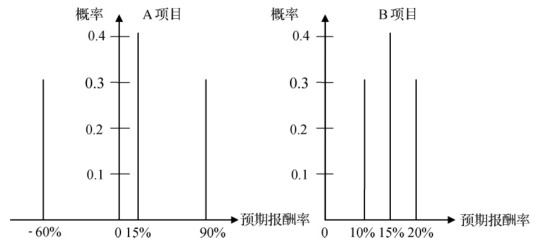
图2-6 离散型分布
实际上,出现的经济情况远不止三种,有无数可能的经济情况会出现。如果对每种情况都赋予一个概率并分别测定其预期报酬率,则可用连续型分布描述,如图2-7所示。
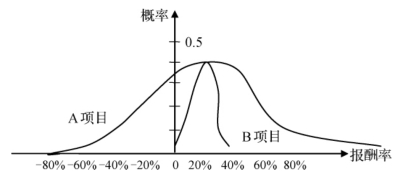
图2-7 连续型分布
(2)期望值
期望值是指可能发生的结果与各自概率之积的加权平均值,反映了投资者的合理预期,用E 表示。根据概率统计知识,一个随机变量的期望值为

【例2-17】 利用例2-16中的数据计算预期年收益的期望值。
解 预期报酬率E(A)=0.3×90%+0.4×15%+0.3×(-60%)=15%
预期报酬率E(B)=0.3×20%+0.4×15%+0.3×10%=15%
两者的预期报酬率相同,但其概率分布不同。A项目的预期报酬率的分散程度大,变动范围在-60%~90%之间;B项目的预期报酬率的分散程度小,变动范围在10%~20%之间。这说明两个项目的预期报酬率相同,但风险不同。为了定量地衡量风险大小,还要使用统计学中衡量概率分布离散程度的指标。
(3)离散程度
一般用方差和标准差来表示随机变量的离散程度。
①方差
方差是离差平方的平均数,分为总体方差和样本方差。

②标准差
标准差是方差的平方根,用来衡量概率分布中各种可能值对期望值的偏离程度。
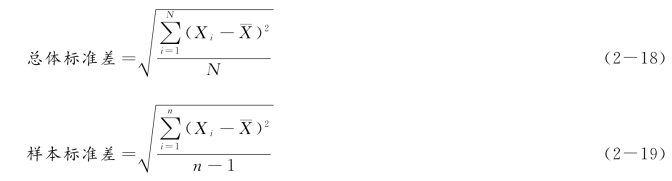
标准差用来反映决策方案的风险,是一个绝对数。在n 个方案的情况下,若期望值相同,则标准差越大,表明各种可能值偏离期望值的幅度越大,结果的不确定性越大,风险也越大;反之,标准差越小,表明各种可能值偏离期望值的幅度越小,结果的不确定越小,则风险也越小。
【例2-18】 利用例2-16中的数据计算标准差(收益率用R 表示,下同)。
解 A项目的标准差是58.09%,B项目的标准差是3.87%,计算过程见下表。由于它们的预期报酬率相同,因此可以认为A项目的风险比B项目的大。
表2-2 A项目预期报酬率的标准差

表2-3 B项目预期报酬率的标准差

标准差是以均值为中心计算出来的,因而有时直接比较标准差是不准确的,需要剔除均值大小的影响。为了解决这个问题,引入了离散系数的概念。离散系数是标准差与均值的比,又称为标准差系数,它是从相对角度观察两者的差异和离散程度,在比较相关事务的差异程度时较之直接比较标准差更好些。
![]()
离散系数是一个相对数,在期望值不同时,离散系数越大,表明可能值与期望值偏离程度越大,结果的不确定性越大,风险也越大;反之,离散系数越小,表明可能值与期望值偏离程度越小,结果的不确定性越小,风险也越小。
【例2-19】 某A 证券的预期报酬率为10%,标准差是12%;某B 证券的预期报酬率为18%,标准差是20%。问A 证券和B证券中哪一个的风险大?
解 离散系数(A)=12%/10%=1.20
离散系数(B)=20%/18%=1.11
直接从标准差看,B证券的离散程度较大,能否说B证券的风险比A 证券大呢?不能轻易下这个结论,因为B证券的期望报酬率较大。如果以各自的平均报酬率为基础观察,A 证券的标准差是其均值的1.20倍,而B证券的标准差只是其均值的1.11倍,B 证券的相对风险较小。这就是说,A 证券的绝对风险较小,但相对风险较大,B证券与此正相反。
2.计算风险报酬率
离散系数虽然能正确评价风险程度的大小,但这还不是风险报酬率。要计算风险报酬率,还必须借助风险报酬系数。风险报酬率、风险报酬系数和离散系数之间的关系为
![]()
【例2-20】 假设上例中A 证券和B 证券的风险报酬系数分别为6%和10%,则两个证券的风险报酬率分别为:
风险报酬率(A)=6%×1.2=7.2%
风险报酬率(B)=10%×1.11=11.1%
由此可以看出,要正确计算风险报酬率,关键在于确定风险报酬系数。风险报酬系数一般可根据以往同类项目的有关数据或由有关专家根据经验和客观情况进行预期确定。
