2.1.2 侧向受荷桩(梁)的基本方程
以直径为d,嵌入长度为L的桩头自由桩(桩头可自由平移和转动)为例,假定桩在地面处受到侧向荷载Pt,弯矩Mt(Mt=Pte,e为Pt作用在地面上的高度)和轴向荷载Q作用,并选定如图2-1所示的坐标系(纵轴为深度x,横轴为桩的侧向变形y,坐标原点位于地面)。由于轴向荷载通常对桩的侧向受荷性状影响较小,假定Q沿桩长相等。考虑桩身x处的单元厚度d x,受力如图2-2所示。
假设桩关于x y平面对称,荷载作用于x y平面内,桩的变形只发生在y轴方向上,即没有平面外的变形,并且忽略桩的剪切变形。以O点为转动中心,由弯矩平衡可得:
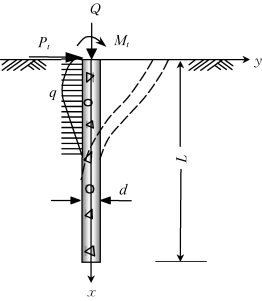
图2-1 侧向受荷桩示意图
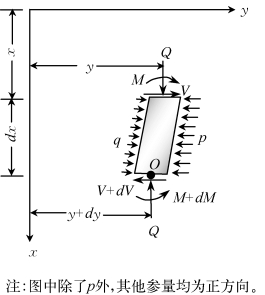
图2-2 侧向受荷桩单元体受力模型(修改自Hetenyi,1946)
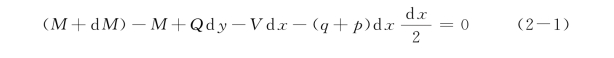
式中,q为桩身分布荷载(FL-1)(如由土体位移、开挖或邻近地面荷载引起的土压力等);其余参量见表2-1。忽略高次微分项(即d x2),式(2-1)可改写为:
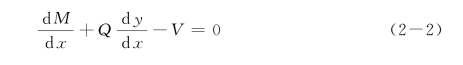
将式(2-2)对x进行再次微分,可得:
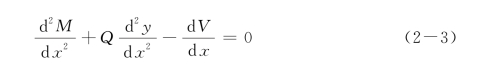
根据图2-2、材料力学知识和Winkler地基梁假定,有:
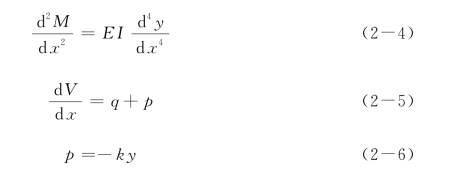
将式(2-4)—式(2-6)代入式(2-3),可得:
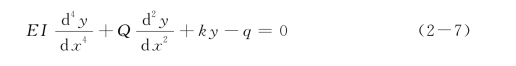
式(2-7)即为侧向受荷桩的变形控制方程。在特定条件下,式(2-7)可简化如下:
(1)对于地面上桩段,此时,ky=0,即有
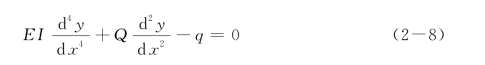
此时,q为地面上作用分布荷载,如由水流或波浪引起的侧向力。
(2)如果分布荷载q为零,式(2-7)可简化为:
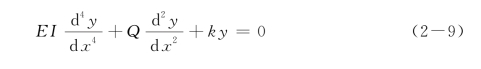
对于均质弹性地基(k值沿深度为常数),如果Q沿桩长不发生变化,Hetenyi(1946)给出了各种桩端约束条件下式(2-9)的理论解答。对于桩头自由的弹性长桩(即半无限长梁),桩的变形解答为:
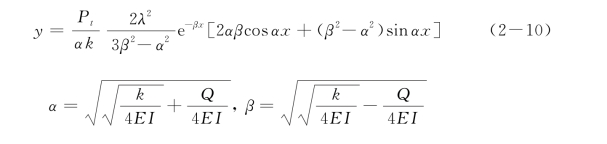
如果y值无限大时,表明桩发生了压缩屈曲,此时,轴向荷载定义为屈曲荷载Qcr。根据式(2-10),可由3β2-α2=0得屈曲荷载:
![]()
另外,对于两端位移自由度固定的有限长桩,屈曲荷载小于或等于(Hetenyi,1946)
![]()
对于其他桩头条件的弹性桩(如桩头固定弹性长桩,桩头弯矩作用弹性长桩),屈曲荷载介于式(2-11)和式(2-12)确定的值之间。
对于常见的侧向受荷桩土系统,桩的轴向承载力或桩头轴向荷载(为了防止桩顶材料应力过高)远比式(2-11)和式(2-12)得到的值小。式(2-10)中的Q/4EI项对桩的变形影响有限,所以通常可不考虑轴向荷载对侧向受荷桩性状的影响。此时,式(2-7)可进一步简化为

如果k沿深度为常数或线性变化,式(2-13)的求解相对比较简单(如Matlock&Reese,1960)。
(3)同样的,如果不考虑轴向荷载的影响,式(2-7)可简化为

式(2-7)、式(2-8)和式(2-14)一般通过数值方法,如差分法(如Gleser,1984;Reese&Van Impe,2001)或有限杆单元法(Mc Vay等,1996)进行求解。
需要指出的是,对于土体引起的分布荷载q,一般可视为k y项的一部分。如在p-y曲线法中,土体抗力p包含土体作用荷载(如主动土压力)和土体对桩施加的反力。因此,在下面的论述中,如果没有特别说明,一般假定q=0。
