6.6.1 San Francisco试验——实例RN1
California交通局在San Francisco进行了两个直径为2.25 m的灌注桩侧向载荷试验(Reese,1997)。桩A和B分别嵌入中等到细粒、薄层状(25~75 mm厚)砂岩内12.5 m和13.8 m。由两个钻孔取出的岩芯可以得出该砂岩为剧烈或中等破碎,并存在层面节理、接缝和破碎区。RQD值为0~80%,平均值为45%。单轴平均抗压强度为0~3.9 m,1.86 MPa;3.9~8.8 m,6.45 MPa;和8.8 m以下,16.0 MPa。然而,在岩层表面(岩层表面下约0.5 m处),代表性的抗压强度qur约为5.7 MPa。由于塑性滑移深度局限于岩层表面,该深度内LFP将采用qur=5.7 MPa进行描述。取RQD=45%,可得不连续结构间距为60~200 mm(Bieniawski,1989)。假定不连续结构其他条件为:表面轻微粗糙,间距<1mm和间隔层高度风化,岩石完全干燥,则可得RMR89=52(Bieniawski,1989)和GSI=47。
表6-16 用于预测桩基性状的其他参数
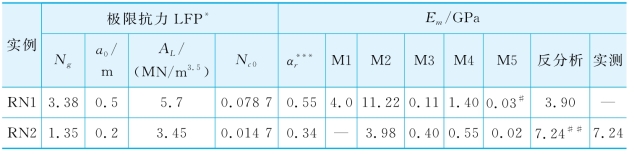
*:对所有实例n=2.5;**:岩石表面下上部三层岩石的平均值;***:如果采用Reese极限抗力时应采用的参数;#:假设为开口接合;##:反算值与报道的值(Reese 1997)一致。
桩A和B通过二者之间的千斤顶同时施加侧向荷载,但Reese(1997)只报道了桩B的性状。因此,本文只对桩B进行分析。桩B的结构组成如图6-34,钢筋笼由40个直径为43 mm的钢筋组成(原文中未报道,故假定为横向加箍),钢筋的强度fy=496 MPa,保护层厚度为0.18 m;混凝土抗压强度fc′=34.5 MPa。开裂前桩截面抗弯刚度E I估计为35.15 GN·m2(Ec=![]() 。侧向荷载作用在岩层表面上1.24 m。
。侧向荷载作用在岩层表面上1.24 m。
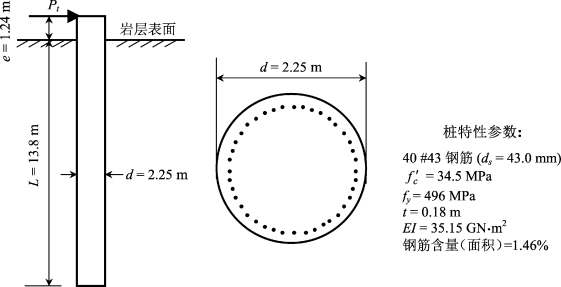
图6-34 San Francisco试验中桩B的结构示意图(未按比例)
未开裂前,混凝土边缘距中性轴距离zt=d/2=1.125 m,根据式(6-2)计算开裂弯矩为4 074~6 518 kN·m(kr=19.7~31.5)。根据钢筋和混凝土的抗压强度,计算得桩截面承压强度Pxu为135.2 MN。
采用第5章实例RS6的线性分析结果,Gm=1.56 GPa(或Em=3.90 GPa),α0=0.5,n=2.5,AL=5.7 MN/m3.5,采用E I值和程序GASLFP计算桩的Pt-y0(岩石表面附近桩的侧向位移)和Pt-Mmax曲线如图6-35所示。
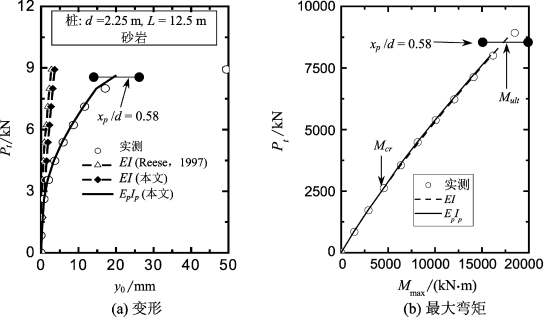
图6-35 San Francisco试验预测与实测桩基性状的比较
从图6-35可以看出,如果忽略桩身抗弯刚度的非线性而采用EI值,尽管预测的最大弯矩与实测值非常吻合(图6-35(b)),但当侧向荷载大于2 620 kN,实测桩顶变形与计算桩顶变形远相差越来越大(图6-35(a))。该结论与Reese(1997)预测的结果相似(图6-35(a))。当Pt=2 620 kN,计算最大弯矩为4 527 kN·m,该值介于4 074~6 518 kN·m之间,因此桩在该荷载水平下可能发生开裂,故可取Mcr=4 527 kN·m和kr≈21.8。
为了考虑桩的结构非线性,采用上述矩形应力块计算方法和相应的程序MUEI,计算极限弯矩和完全开裂后抗弯刚度,其中β1=0.85-0.05(fc′-27.6)/6.9=0.80。表6-17列出了3个代表性的迭代计算步。当θ=3.11×10-3m-1时,c=1.125 m,中性轴与中心轴重合,承受压力和拉力的钢筋数量相等,因此钢筋提供的总轴力Pxs=0,此时|Pxs+Pxc-Px|=37 008>0.000 01Pxu=1.35 kN(由于没有施加轴力,Px=0),轴向力不平衡,迭代未收敛。当θ增加到6.72×10-3m-1,|Pxs+Pxc-Px|=0.7 kN≤0.000 01Pxu=1.35 kN,迭代达到了收敛标准,故轴向力近似达到平衡。相应地,c=0.521 m,a=0.416 m,名义极限弯矩Mn=21.57 MN·m。在受拉侧,最边缘钢筋的拉应力εs1为6.2×10-3,ψ=0.483+83.3εs1=0.999 5>0.9,因此取ψ=0.9。由式(6-11)得Mult=19.413 MN·m。
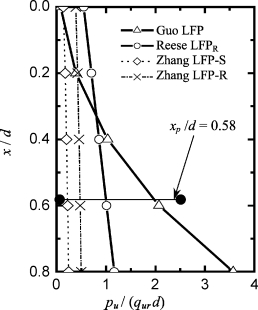
图6-36 San Francisco试验的LFP
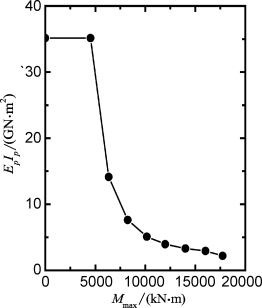
图6-37 San Francisco试验的EpIp
表6-17 San Francisco试验实例中Mult的计算
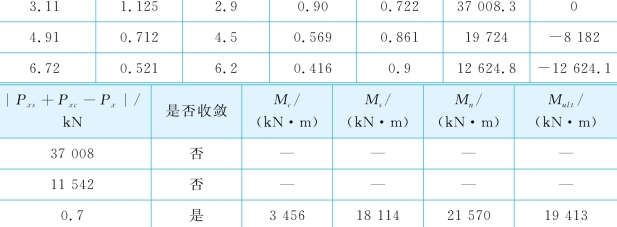
在最大荷载Pt=9.0 M N时,采用EI值计算得到的最大弯矩为18 188 kN·m。该值比Mult值小6.3%。然而,从实测结果发现,当Pt从8.0 MN增加到9.0 MN时,桩顶变形剧烈增加,表明桩已经发生了弯曲破坏。也就是说,在该实例中,由MUEI预测的极限弯矩略微偏高。考虑到本实例中,大直径灌注桩在施工过程中可能引起较大的不确定性,将ψ值降低10%,即取ψ=0.81,此时有Mult=17.472 MN·m,该值与Reese(1997)报道的极限弯矩17.74 MN·m非常一致。完全开裂后等效抗弯刚度(E I)cr=17.472/6.72×10-3=2.6GN·m2,此时,(EI)cr/EI=0.074。采用上述岩体杨氏模量,极限抗力分布和EI值,由Mult=17.472 MN·m和程序GASLFP反算得到极限侧向荷载为8.62 MN。
采用上述Gm值和LFP,考虑桩身抗弯刚度的非线性特性,对于每一荷载,采用程序GASLFP或FDLLP桩顶位移按如下步骤重新预测:①采用EI值得到该荷载对应的最大的弯矩Mmax;②按式(6-3)计算Ie和等效抗弯刚度EpIp(=EcIe);③采用EpIp值和程序GASLFP或FDLLP计算桩顶变形和最大弯矩。本例采用程序GASLFP,计算结果如表6-17。计算EpIp值、桩顶变形和最大弯矩分别绘于图6-37和图6-35。从图6-35可见:①计算桩顶变形和最大弯矩与实测结果非常吻合;②采用E I值和EpIp值计算得到的最大弯矩相差2.2%以内。因此,如前所述,不考虑开裂的影响,采用EI值预测桩身最大弯矩是准确的。然而,桩身抗弯刚度由于开裂而引起的降低对变形和塑性滑移深度影响比较显著。如在极限荷载Pt=8 620 kN时,采用EI值和EpIp值得到的桩顶最大变形分别为3.5 mm和19.9 mm(大约增长了4.7倍),滑移深度分别为0.887 m(=0.39d)和1.312 m(=0.58d),增长了47.9%。
在极限荷载塑性滑移深度内,归一化极限岩体抗力pu/(qurd)与Zhang等(2000)提出的岩体极限抗力(Zhang LFP-S为光滑嵌固LFP;Zhang LFP-R为粗糙嵌固)一同绘于图6-36。对于Zhang LFP,确定参数如下:mi=19(Hoek&Brown,1988),mb=2.862,s=0.002 77和m=0.5。可见,在0.58d深度内:①反分析得到的pu/(qurd)从岩层表面处的0.08逐渐增加到0.58d处的1.95;②反分析得到的pu/(qurd)可近似采用Reese极限抗力进行平均,此时,αr=0.55;③Zhang LFP-S和Zhang LFP-R平均值小于反分析pu/(qurd)的平均值,因此,它们将给出过大的桩顶位移。
