8.2 理想弹塑性p-y曲线与硬化p-y曲线的比较
对于海洋钙质砂的p-y曲线,目前主要有三种,如表8-1所列,分别编号为CSPY1—CSPY3。为了对这些p-y曲线与本文采用的理想弹塑性p-y曲线进行比较,假定如下实例：桩径d=2.08 m,e=0和Ep=3.0×104MPa;土体参数接近澳大利亚巴士海峡Kingfish B石油平台(以下简称Kingfish B砂)附近的钙质砂,选取参数如下：有效容重γs=8.1 kN/m3,φ=31°,Gs=5.0 MPa,νs=0.3,n=1.7,α0=0和Ng=0.33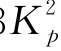
p,并且,静力触探贯入阻力qc以400 kPa/m的斜率线性增长。
表8-1 静载钙质砂中侧向受荷桩的p-y模型
绘制表8-1中三种模型以及理想弹塑性模型在x=2d处的p-y曲线,如图8-1所示,可以发现：①在y/d小于0.5%时,四种p-y曲线非常接近;②当y/d大于0.5%时,对于CSPY1—CSPY3模型,土体抗力随变形无限地增长,而理想弹塑性p-y曲线则由于达到极限抗力而保持不变。因此,相对于理想弹塑性模型,CSPY1—CSPY3模型可统称为硬化p-y模型。
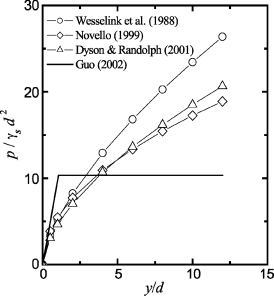
图8-1 x=2d处p-y曲线(d=2.08 m)
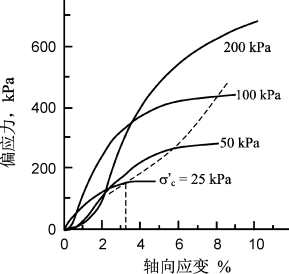
图8-2 Kingfish B砂偏应力-应变关系(Hudson等,1988)
与硬化p-y模型不同,理想弹塑性p-y曲线与钙质砂的应力应变曲线十分相似。图8-2所示为Kingfish B砂典型的应力应变关系曲线(Hudson等,1988)。在围压小于100 kPa时,应力随应变在初始阶段近似线性增长;当达到一定的应变后,应力达到峰值偏应力,然后缓慢增长或几乎保持不变。在图8-2中,虚线为峰值偏应力点的连线。峰值偏应力连线与各应力应变曲线交点对应的应变可视为屈服应变εu。根据p-y曲线与土体应力应变关系的相似性(McClelland&Focht,1958),屈服应变εu可等效为侧向受荷桩的无量纲变形yu/d,其中yu为土体达到极限抗力时的桩基变形。对于围压σ3=25～100 kPa时,屈服应变约为3%～8%(图8-2)。除了Kingfish B砂外,其他海洋钙质砂也表现出同样的特性,如Leighton buzzard,Dogs Bay,Ballyconneely和Bombay Mix.钙质砂(Golightly&Hyde,1988)也存在屈服应变,在σ3=5～100 kPa时,εu为2%～7%。因此,对于钙质砂中的侧向受荷桩,土体同样存在极限抗力。所以,理想弹塑性p-y曲线比硬化p-y曲线更合理。
尽管表达式不同,通过调整表达式中的参数,上述三种硬化p-y模型能给出比较一致的p-y曲线。因此,下面只比较采用CSPY1模型和理想弹塑性p-y模型得到的桩基特性。将CSPY1产生的p-y曲线输入到程序COM624P(FHWA,1993)计算得到桩的性状,如图8-3所示。同时,采用GASLFP和理想弹塑性p-y曲线得到的结果也绘于图8-3。
将Ep=3.0×107kPa和Gs=5.0 MPa代入式(2-19),计算得桩的有效长度Lcr=11.33d=23.57 m。从图8-3(c)—(e)也可以看出,桩的变形、土体抗力和弯矩主要发生在Lcr深度内。
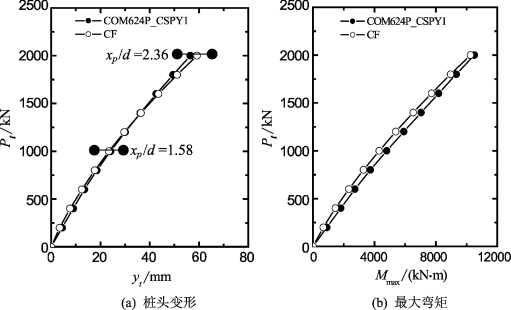
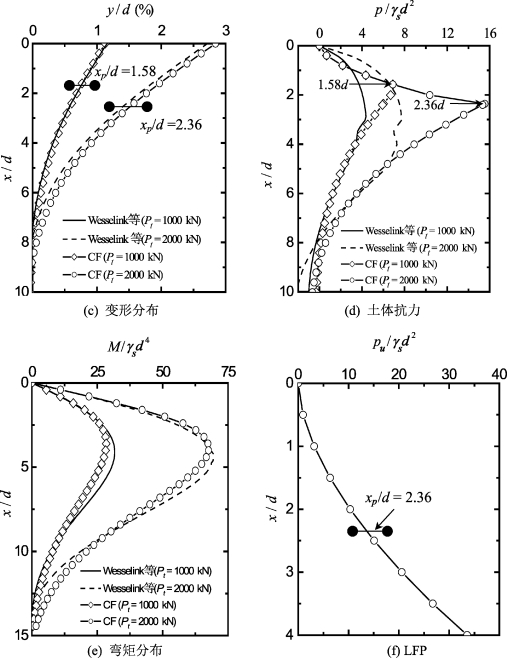
图8-3 采用理想和硬化p-y模型预测桩基性状的比较
从图8-3可见：①尽管p-y曲线不同,上述两种模型能给出一致的桩头变形(图8-3(b))、变形(图8-3(c))和弯矩(图8-3(e))分布;②土体抗力沿深度分布不同而不同,与所采用的p-y模型十分相关(图8-3(d))。对于CSPY1模型,土体抗力沿深度缓慢增长;而对于理想弹塑性p-y模型,土体抗力从零(地面处)增长到滑移深度xp处的最大值(对于Pt=1 000 kN和Pt=2 000 kN,xp分别为1.58d和2.36d),然后随深度增加而降低。在深度xp处出现剧烈变化,主要是由于理想弹塑性p-y模型未考虑弹性与塑性之间的过渡段(如第4章所述,这对桩的性状影响很小);(3)最大弯矩发生深度xmax也与所采用的p-y模型有关(图8-3e)。如在Pt=2 000 kN时,采用理想p-y模型和CSPY1模型,xmax值分别为9.3 m(4.47d)和8.06 m(3.88d)。
根据第2章的桩的分析,土体抗力为弯矩的二次导数。因此,由实测离散的弯矩点确定土体抗力会存在很大的不确定性。采用同一组数据,如果采用不同的函数拟合实测弯矩点,然后二次求导将得到显著不同的土体抗力。因此,单纯由实测的桩顶变形或弯矩大小(注意在试验中为离散值)确定p-y曲线往往不是唯一的。真实的p-y曲线必须与实测的土体抗力相吻合,同时能够反映桩土相互作用性状,如塑性区的存在。