4.3.2　桩的离散与土体反应

下面考虑长为L+e(其中,L为嵌入长度,e为地面上桩长)的桩(图4-3),受到地面上集中荷载P1,P2,…,Pm作用,作用高度分别为e1,e2,…,em。采用差分法求解时,将桩分为t等分,每等分的高度为h=(L+e)/t,编号如图4-3所示。在地面下共有p等分,因此在地面上有t-p等分。为了采用差分法求解,桩顶上(t+1和t+2)和桩端下(-1和-2)分别添加两个虚拟等分点。

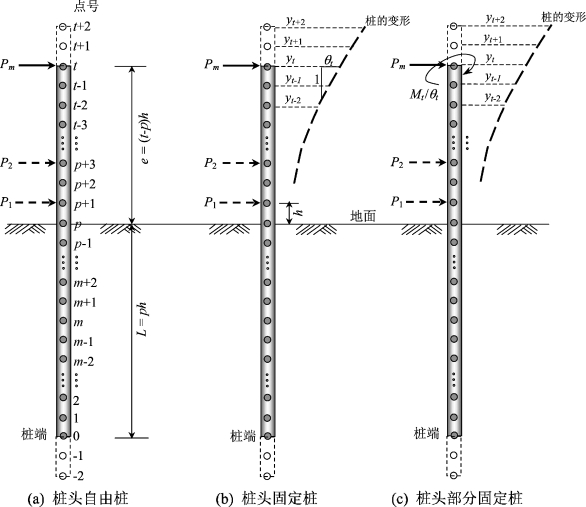
图4-3　统一差分法计算桩的性状

采用如图4-1(b)或图4-2(b)所示的桩土相互作用模型,并不考虑虚拟膜的存在。在弹性状态时,地基反力模量为k;达到塑性状态时,土体极限抗力由统一极限抗力分布模式确定。以x=xm+2,xm+1,xm,xm-1和xm-25点为例,各点的变形和p-y曲线如图4-4(b)所示。图中每一条p-y曲线描述了某点处的桩土相互作用性状。并且每条p-y曲线似乎只与所在深度有关,但实际上,通过选取考虑土体连续性的地基反力模量(如式(2-35)和式(2-45))可以一定程度上考虑邻近土体对考察点处p-y曲线的影响。并且,试验还表明,某一点处的地基反力主要与该截面处桩的变形大小有关(Reese,1977)。因此,在理论分析时,可以用图4-4(b)中的p-y曲线代替连续的土体。值得说明的是,在采用差分法求解时,每一点的地基反力模量k和极限抗力可以采用与图4-1(b)或图4-2(b)所示模型不同的值,从而更准确地考虑分层土体和其他效应的影响。

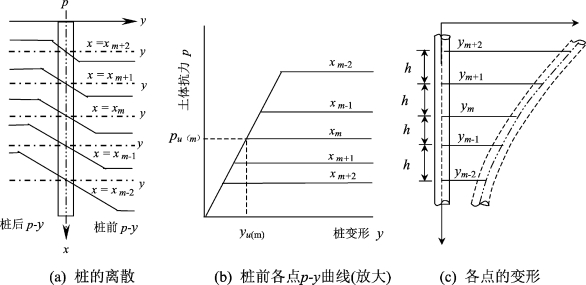
图4-4　桩的离散和各点处的理想弹塑性p-y曲线