7.2.1 群桩的试验性状
由于土体的空间变异性大、本构模型复杂(如考虑桩的施工效应),目前还没有普遍接受的计算群桩效率系数的理论解答。因此,对于群桩的分析,大部分都基于试验研究和数值模拟。下面主要介绍试验观测的群桩效率系数和荷载分配关系。
为方便论述,下面将群桩称为mg×ng群桩,其中,mg=群桩的排数,ng=每排上的桩数。例如,图7-1(a)所示为3(mg)×2(ng)群桩,荷载方向和垂直荷载方向上间距分别为ss(排距)和sp(列距)。如果ss=sp,可简称为中心距为s的mg×ng群桩。如果mg=1或ng=1,一般称为排桩。如果排桩的中心连线与加载方向一致,称为串联排桩;如果排桩的中心连线与加载方向垂直,称之为并联排桩(Rao,1996)。因此,群桩可视为多个串联排桩或多个并联排桩组成。在排桩的分析基础上,可对群桩分析进行一定的简化。
国内外一些研究者对排桩进行了室内和现场载荷试验(Prakash,1962;Schmidt,1981,1985;Cox等,1984;Wang& Reese,1986;Franke,1984,1988;Shibata等,1989;Rao等,1996)。报道的并联排桩和串联排桩效率系数分别见表7-1和表7-2。根据这些试验,排桩存在如下特性:
(1)对于不同的群桩位移水平,群桩效率系数差别不大(Cox等,1984;Reese&Van Impe,2001);
(2)群桩效率系数随桩中心距的变化比一些弹性方法(如Poulos,1971b)或半经验半理论方法,如Focht-Koch-Poulos方法(Focht& Koch,1973),预测的结果平缓(Schmidt,1981,1985;Reese&Van Impe,2001);
(3)对于砂土和黏土中的并联排桩,如果邻近桩间没有净距,ηg近似为0.5(Wang&Reese,1986)。因此,如果不考虑施工加密效应和承台影响,群桩的效率系数ηg一般为0.5~1.0;
(4)群桩效率系数可能与土体、桩的施工条件、桩长等有关(Schmidt,1981,1985;Reese&Van Impe,2001);
(5)对于并联排桩,当sp/d≥3时,各桩分配的荷载差别很小(Prakash,1962;Franke,1988),并且各桩近似为独立单桩,ηg值近似为1.0(Wang &Reese,1986;Shibata等,1989);
(6)对于串联排桩,前排桩性状如同独立单桩(Franke,1988;Schmidt,1981,1985),后排桩的存在导致ηg值小于1(Reese&Van Impe,2001);
(7)对于串联排桩,当中心距大于1.5时,各后排桩的效率系数差别不是太大(Cox等,1984;Reese&Van Impe,2001);
(8)对于串联排桩,当ss/d>5~8时,ηg=1.0(Prakash,1962;Schmidt,1981,1985;Franke,1988;Shibata等,1989;Rao等,1996);
(9)对于存在刚性承台的群桩,各桩弯矩差别较小,尽管桩顶分配的荷载大小不同(Schmidt,1981,1985;Reese&Van Impe,2001)。
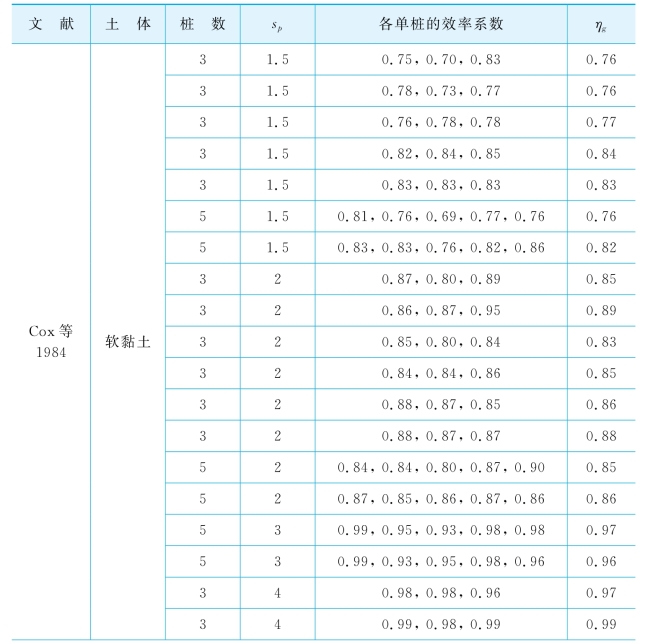
表7-1 并联排桩的效率系数(资料来源Reese&Van Impe,2001)
续表

续表
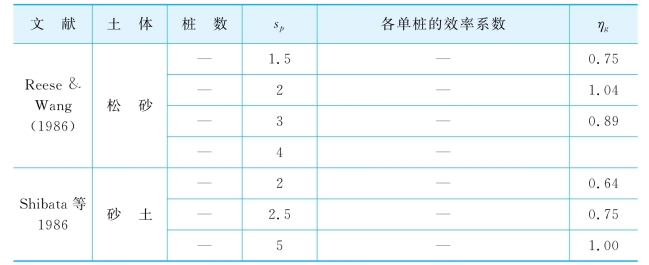
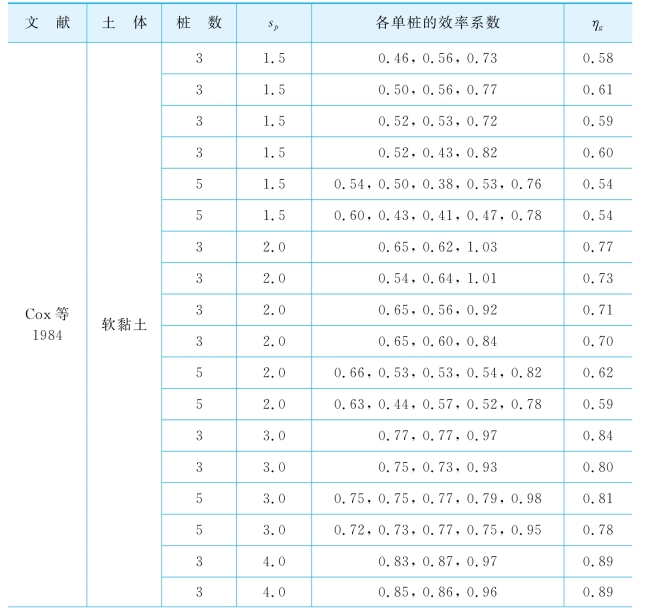
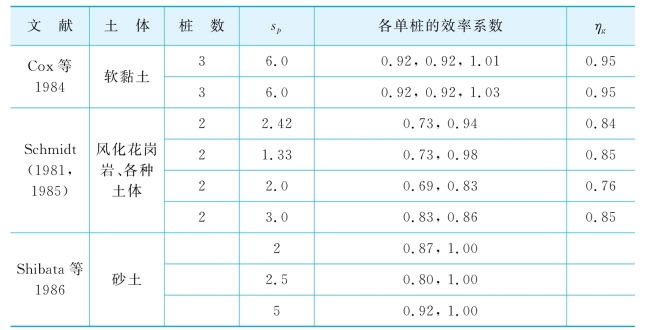
表7-2 串联排桩的效率系数(资料来源Reese&Van Impe,2001)
续表
除了排桩的试验研究外,部分研究者还对矩形分布(mg>1,ng>1)的群桩进行了试验研究(如Brown& Reese,1987,1988;刘金砺,1992;Mc Vay等,1994;Mc Vay等,1995;Mc Vay等,1998;Ruesta&Townsend,1997;Rollins等,1998),发现了如下现象:
(1)ηg值一般小于1.0,但由于群桩施工引起土体加密和承台效应,也会导致ηg值大于1.0(刘金砺,1992);
(2)群桩效率系数随间距的增大而增长。如在Mc Vay等(1995)试验中,3d和5d的3×3群桩效率系数分别约为0.74和0.93;
(3)前排桩比后排桩承担的荷载大;
(4)对于mg≥3的群桩,中间排桩与后排桩承担的荷载没有确定的大小关系,有时中间排桩比后排桩承担的荷载大(Brown& Reese,1987,1988;Mc Vay等,1995),有时,后排桩比中间排桩承担的荷载大(Rollins等,1998;Brown等,2001);
(5)在各排内,边桩比中间桩承担的荷载大(如Brown& Reese,1987),但差别不是太大(Mc Vay等,1998);
(6)前排桩与后排桩的载荷-变形曲线相似,但前排桩比后排桩承担较大的荷载,前排桩的最大弯矩比后排桩大(Ruesta&Townsend,1997);
(7)土体密度对荷载分布有一定的影响(Mc Vay等,1994;Mc Vay等,1995)。在较大的密度下,前排桩承担更大的荷载;在较小的密度下,各排之间的荷载分配趋于均匀。如间距分别为3d的3×3群桩(Mc Vay等,1995),在密砂中,前排桩、中排桩和后排桩分别承担了45%,32%和23%的总荷载;在中密砂中,前排桩、中排桩和后排桩的荷载分担比分别为37%,33%,和30%。因此,随着密度的降低,各排桩之间的荷载分担比趋于一致;
(8)在给定的桩基变形条件下,各单桩的土体抗力,随桩间距的增加而增长(Mc Vay等,1994)。
根据上述排桩和矩形分布群桩的试验现象,可得出如下结论或合理的假定:
(1)群桩效率系数近似与位移水平无关;
(2)不考虑施工加密效应和承台效应,群桩的变形和弯矩比单桩大,即ηg值小于1.0;
(3)当ss/d≥6和sp/d≥3时(即大间距群桩),可不考虑群桩的遮拦效应,ηg=1.0;
(4)群桩的荷载分担表现为“前排大、后排小”的规律;
(5)一般可将前排边桩视为单桩,带刚性承台的前排边桩即为桩头固定的单桩;
(6)当sp/d≥3时,各排内的桩承担荷载近似相等。
