2.4.4 Guo&Lee(2001)
在Sun的研究基础上,Guo&Lee(2001)对双参数法作了进一步完善。对于均质、各向同性、线弹性土体(剪切模量为Gs,泊松比为νs)中长为L,半径为r0的侧向受荷圆形桩(图2-13),采用柱坐标r,θ和z,忽略侧向荷载引起的竖向位移w,土体径向位移u和环向位移v可表达为傅立叶级数形式：
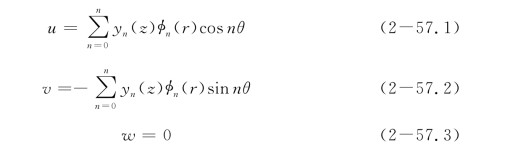
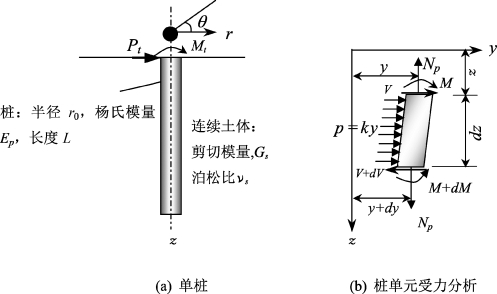
图2-13 桩土相互作用系统(Guo&Lee,2001)
式中,yn(z)为深度z处桩身变形的第n个分量,发生在第n个荷载作用方向上;φn(r)为离桩轴径向距离为r处土体位移消减函数;θ为桩截面中心与研究点连线与第n个荷载作用方向的夹角。对于只有荷载Pt和弯矩Mt作用条件下,n=1。如果考虑在不同的“θ”方向上施加荷载和弯矩作用,就需要考虑其他项(如n=2,3),此时,位移和应力计算符合叠加原理。
对于侧向受荷桩,由于土体泊松比νs影响较小(Poulos,1971a),Guo&Lee(2001)采用等效剪切模量G*=Gs(1+0.75νs)(Randolph,1981)代替实际的剪切模量Gs和νs。对于n=1的情况,取νs=0,桩周土体应力场可表达为：
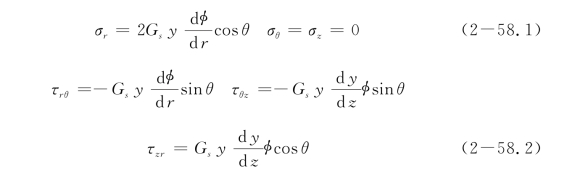
以桩土相互作用系统为研究对象,根据虚功原理,得到与式(2-9)相似的桩基变形控制方程：
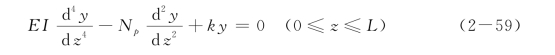
和土体径向位移消减函数控制式(2-54),式中,k等效为Winkler地基模型的地基反力模量;Np为弹簧间(虚拟膜)传递的轴向拉力。k和Np可表达为：
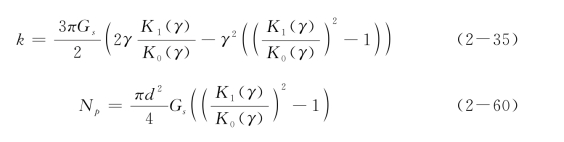
其中,γ为荷载传递系数,γ=k1(Ep/G*)k2(L/r0)k3,k1,k2和k3如表2-10所列。
对于
,Guo&Lee(2001)结合式(2-54),推导了式(2-59)的统一解答：
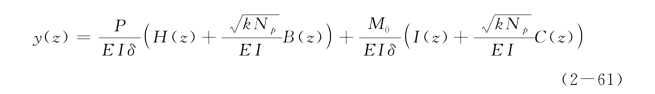
式中,H(z)和I(z)为反映桩头约束条件的函数;B(z)和C(z)为反映桩端约束条件的函数;对于给定的桩端约束条件,H(z),I(z),B(z),C(z)和系数δ可表达为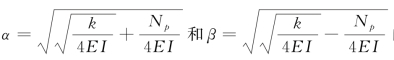
的函数,详见Guo&Lee (2001)。对于桩身转角、弯矩、剪力和土体抗力可通过式(2-15)—式(2-18)确定。
与Sun的解答比较,Guo&Lee不仅解决了较大νs值时解答的奇异性,而且给出了桩基性状的代数表达式,不需迭代求解。
上述四种解答,基本上覆盖了基于弹性地基梁法和双参数法的侧向受荷桩所有解答。