6.3.3 与COM624P和Florida-Pier的比较
在下面的实例分析中,将采用本文方法分析砂土中单桩的非线性性状,并与程序COM624P和Florida-Pier(简化为FLPier)的分析结果进行比较。COM624P(1993)是美国高速公路管理局(FHWA)提供的Dos版程序,其中桩土相互作用采用Reese等(1974)提出的砂土p-y曲线模型,桩的结构非线性分析基于Hognestaad抛物线型混凝土应力应变关系,桩变形方程的求解方法为有限差分法。FLPier是Florida大学开发的用于分析桩与桥墩共同作用的软件,桩土相互作用可采用Reese等(1974)或O'Neill& Murchison(1983)提出的砂土p-y曲线模型,桩的结构非线性分析基于Hognestaad抛物线型混凝土应力应变关系,桩与桥墩的相互作用采用三维非线性有限元方法求解。
桩的结构组成如图6-3所示,钢筋笼由12个直径为25.4 mm的钢筋组成,钢筋笼横向加箍,钢筋保护层厚度为76.2 mm。钢筋的强度fy=413.69 MPa,混凝土抗压强度f′c=34.47 MPa。开裂前桩截面抗弯刚度EI估计为
10-3m4)。土体为水下均质砂土,φ=39°,有效容重γs=15.2 kN/m3,νs=0.3。侧向荷载作用在地面上0.838 m。
Hoit等(1996)分别采用程序COM624P和FLPier对上述实例进行了桩的线性(FLPier_EI和COM624P_EI)和非线性分析(FLPier_EpIp和COM624P_EpIp),见图6-4。
采用本文方法,分析如下：
(1)对于水下中密砂,COM624P采用线性增长的地基反力模量,即k=nhx,nh=16.3 kN/m3,8d深度内的平均地基反力模量为33.12 MPa。假设该土体为地基反力模量为33.12 MPa的均质砂土,由GASLFP计算得Gs约为10.0 MPa;
图6-3 桩的结构示意图(未按比例)
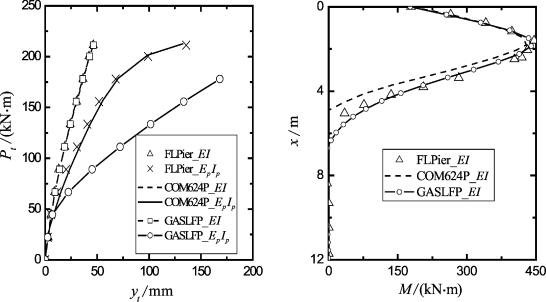
图6-4 桩的线性分析和非线性分析比较
(2)采用α0=0和n=1.7,通过比较FLPier或COM624P线性分析结果,由程序GASLFP反分析得到：Ng=0.55K2p。同时得到线性分析桩顶位移(图6-4(a))、桩身最大弯矩Mmax和弯矩分布(图6-4(b))。除了桩顶位移,采用程序GASLFP得到的弯矩分布也与FLPier计算结果非常吻合;
(3)当kr=19.7～31.5时,根据式(6-2)计算开裂弯矩为47.1～75.3 kN·m,其中混凝土边缘距中性轴距离zt=d/2=254 mm。由程序GASLFP分析得开裂荷载Pcr=31.5～47.3 kN。与FLPier或COM624P的线性和非线性比较,可以发现,由FLPier或COM624P得到的开裂荷载位于该区间内。因此,下面取平均值Mcr=61.2 kN·m(Pcr=39.4 kN)进行非线性分析;
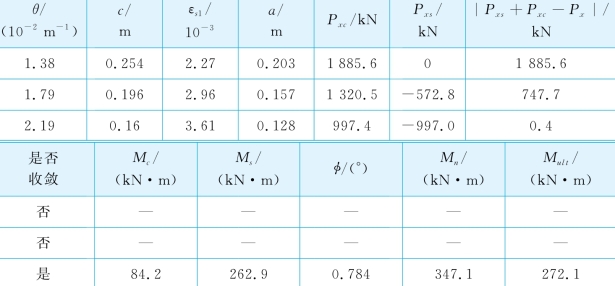
(4)为了考虑桩的结构非线性,采用上述矩形应力块法和相应的程序MUEI,计算极限弯矩和完全开裂后抗弯刚度,其中,β1=0.85-0.05(fc′-27.6)/6.9=0.80。表6-4列出了3个代表性的迭代计算步。由桩截面尺寸、钢筋和混凝土的强度,计算得Pxu=6 780 kN。采用0.000 1Pxu作为轴向力平衡收敛标准。当θ=1.38×10-2m-1时,c=0.254 m,中性轴与中心轴重合,承受压力和拉力的钢筋数量相等,因此,钢筋提供的总轴力Pxs=0,此时,|Pxs+Pxc-Px|=1 885.6＞0.000 1Pxu=0.68 kN(其中,Px=0),轴向力不平衡,迭代未收敛;当θ增加到2.19×10-2m-1,|Pxs+Pxc-Px|=0.4＜0.68 kN,迭代达到了收敛标准,轴向力近似平衡。相应地,c=0.16 m,a=0.128 m,名义极限弯矩Mn=347.1 kN-m。在受拉侧,最边缘钢筋的拉应变εs1为3.61×10-3,则φ=0.483+83.3εs1=0.784。由式(6-11)和式(6-12)得：Mult=272.1 kN·m和(E I)cr=12.4 MN·m2。Mult值比采用COM624P(1993)计算得到的极限弯矩(约428.9 kN·m)小。如同实例2,考虑COM624P的内部计算错误,将该极限弯矩乘以0.737得修正后的极限弯矩为316.1 kN·m,比采用MUEI得到的极限弯矩大12%;
表6-4 Mult的计算过程
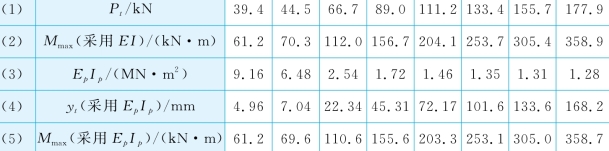
(5)采用上述土体参数、Gs值和LFP,考虑桩的结构非线性,采用程序GASLFP重新计算桩顶位移和弯矩,如表6-5。对于大于Pcr的每一级荷载(行1),采用步骤2得到的最大弯矩Mmax(行2),按式(6-5)计算等效抗弯刚度EpIp(行3)。然后采用EpIp值计算桩顶变形(行4)和最大弯矩(行5)。将计算得到的Pt-yt曲线也绘于图6-4。
表6-5 考虑桩结构非线性计算桩顶位移
根据上述分析和计算结果,可以得出如下讨论：
(1)采用EI值和EpIp值计算得到的最大弯矩相差1%以内。因此,不考虑混凝土开裂的影响,直接采用开裂前的抗弯刚度EI值预测桩身最大弯矩是准确的;
(2)与程序FLPier和COM624P相比,采用ACI方法计算开裂弯矩Mcr是准确的;
(3)与实例2的讨论相似,采用MUEI计算得到的极限弯矩和开裂后等效抗弯刚度与修正后的COM624P结果比较一致;
(4)采用式(6-5)得到的等效抗弯刚度计算桩的非线性变形比COM624P预测的结果大。这可能存在如下原因：①由于程序COM624P计算的极限弯矩过高(注意图6-4中采用COM624P的非线性分析结果没有考虑极限弯矩的修正);②由式(6-5)计算的等效抗弯刚度可能偏小。后者将在下面的实例分析中进一步讨论;
(5)同样地,采用式(6-5)得到的等效抗弯刚度计算桩的非线性变形比Hoit等(1996)采用FLPier计算的结果大(图6-4(a))。