4.4 GASLFP,FDLLP与COM624P
COM624P是美国高速公路局(FHWA,1993)推荐使用的侧向受荷桩分析程序。该程序存在如下特性：①地基反力模量随深度线性增长,k=nhx;②采用一系列分段p-y曲线,如图4-1(c)中的曲线B,能够考虑弹性与塑性之间的过渡区;③采用砂土Reese LFP,黏土Matlock LFP和R-C LFP;④差分法求解。COM624P与GASLFP和FDLLP的对比见表4-2。下面用一个假想的实例对三者的分析结果进行比较。
表4-2 GASLFP,FDLLP与COM624P程序的区别
续表
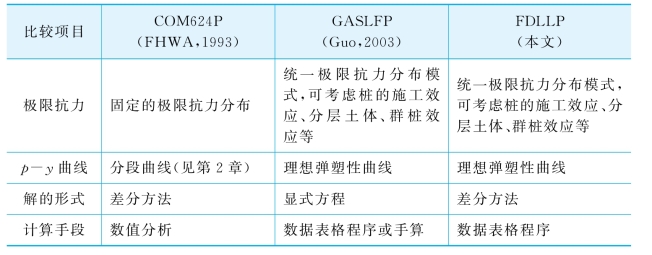
假想实例的桩基和土体特性如下：一钢管桩,长15.2 m,桩外径0.373 m,壁厚22.5 mm,桩截面惯性矩为8.084 5×10-4m4,抗弯刚度EI=80.0 MN·m2,则Ep=EI/(πd4/64)=2.40×104MPa;土体为均匀级配中密细砂,内摩擦角为35°,浮容重为9.9 kN/m3,泊松比为0.3。荷载作用在地面处。
采用COM624P分析时,参数如下：地基反力常数nh=16.3 MN/m3;采用缺省的极限抗力分布LFP,即砂土Reese LFP。并在表4-3和图4-5中表示为‘COM624P’。
采用GASLFP分析时,选取Gs=11.2 MPa,此时由式(2-35)计算得k=30.4 MN/m2,该值与采用COM624P分析时,10d深度内k的平均值相等(由nh=16.3 MN/m3计算得到)。极限抗力分布(LFP)由α0=0,n=1.7和Ng=0.45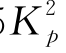
确定,相应的LFP与Reese LFP(COM624P缺省采用)几乎一致,如图4-5(a)所示。相应的预测结果表示为‘CF,Case III’。
采用FDLLP分析时,取Gs=11.2 MPa,采用式(2-45)计算得：k=43.1 MN/m2,忽略弹性状态时弹簧间的耦合效应,即Np=0;并采用与GASLFP相同的LFP。在表4-3和图4-5中表示为“FDLLP”。
图4-5(b)给出了深度分别为1.0 m和3.0 m深度处COM624P和GASLFP采用的荷载传递p-y曲线。FDLLP与GASLFP采用的p-y曲线相似,但弹性阶段的斜率(地基反力模量k)稍有不同。可见,COM624P和GASLFP采用的p-y曲线是不同的：COM624P采用的p-y曲线考虑了弹塑性过渡区,并且弹性地基反力模量随深度线性增长,而GASLFP或FDLLP采用的p-y曲线是理想弹塑性模型,未考虑弹塑性过渡区,并且弹性地基反力模量沿深度不变。但三者采用的极限抗力是比较接近的。
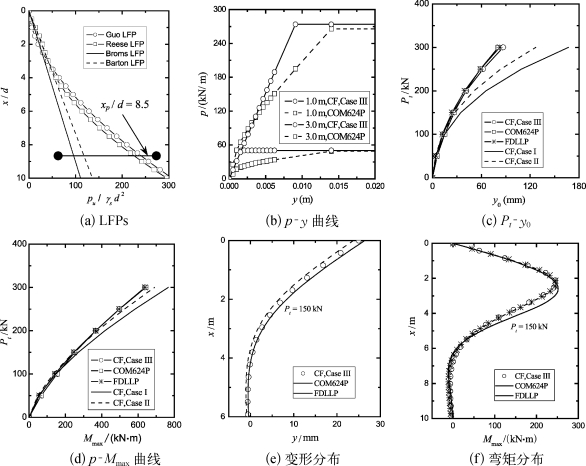
图4-5 极限抗力分布与不同计算模型对桩基性状的影响
表4-3 分析假想实例时采用的不同LFP
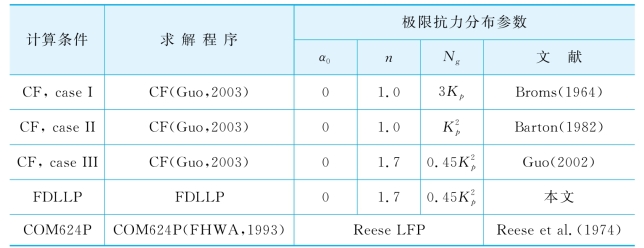
图4-5(c)—(f)分别给出了采用上述计算条件得到的Pt-y0,Pt-Mmax关系曲线以及Pt=150 kN时变形和弯矩沿深度分布。可以发现：
(1)尽管p-y不同(LFP相似,k不同,弹塑性过渡区不同),但CF,Case III与COM624P预测的结果十分吻合。由于二者分别采用了两种极端的地基反力模量分布模式(一般的地基反力模量分布介于沿深度线性增长和常数之间),因此,桩基的性状主要由LFP控制,而不是弹性地基反力模量或弹塑性过渡区。
(2)CF,Case III与FDLLP预测的桩基性状相当一致。因此,在一般条件下,弹簧间的耦合效应对桩的性状影响可忽略不计。
(3)在最大荷载Pt=300 kN时,塑性滑移深度xp=3.19 m(8.5d),Mmax=637.9 kN·m,y0=86.8 mm≈23.3%d。y0值大于一般的桩基设计标准(如10%d或20%d)。因此,结论(1)和(2)不仅适用于较小荷载水平,也适用于设计直到破坏荷载水平。
为了进一步研究LFP对桩基性状的影响,采用程序GASLFP和Broms LFP(Broms,1964)和Barton LFP(Barton,1982),对上述桩基性状进行了分析,分别表示为CF,Case I和Case II。在这两种计算条件下,Gs值与CF,Case III的Gs值相同。从图4-5可见,CF,Case I远大于CF,Case III预测的桩顶变形。在Pt=300 kN时,CF,Cases I预测的y0=167.0 mm和Mmax=766.2 kN-m,分别达到了CF,Cases III预测结果的1.9倍和1.2倍。由于CF,Cases II的LFP较接近于CF,Cases III的LFP,CF,Cases II比CF,Cases I更接近于CF,Cases III的预测结果。因此,不同的LFP,将给出不同的桩基的性状。
为比较地基反力模量和LFP对桩基性状的影响,以上述FDLLP计算实例为基准,采用程序FDLLP计算,当Gs和Ng值分别增加和降低50%后,桩头变形和最大弯矩的比较如图4-6所示。为此,可以得出如下结论：
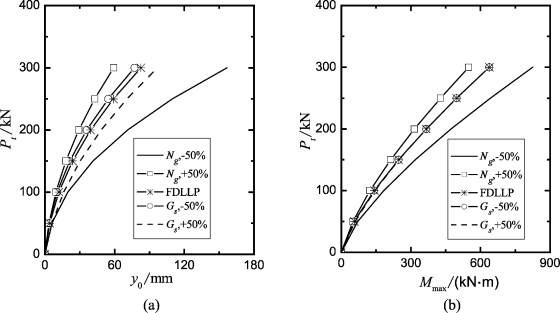
图4-6 LFP和Gs值对桩基性状影响的比较
(1)桩头侧向变形随Ng和Gs值的增长而降低(图4-6(a))。
(2)桩头侧向变形对Ng值的变化远比Gs值的变化敏感。如当Pt=300 kN,Ng值降低50%时,y0=156.6 mm,而Gs值降低50%时,y0=96.8 mm。与Gs和Ng值未发生变化时(y0=82.6 mm)比较,分别增长了90%和17%。可见,准确选择Ng值远比确定Gs值对桩头变形重要。
(3)桩的最大弯矩随Ng值的增长而降低,随Gs值的变化而几乎不发生变化。如当Pt=300 kN时,N g值降低50%时,M max=824.6 kN·m,而Gs值降低50%时,Mmax=637.9 kN·m。与初始Gs和Ng值对应的结果(Mmax=637.9 kN·m)比较,分别增长了29.3%和零。因此,在较大荷载水平下,桩的最大弯矩只取决于土体极限抗力的分布。所以,在确定土体的极限抗力时,优先比较实测和预测的荷载-最大弯矩关系。
(4)从结论(2)和(3)可进一步发现,Ng值的变化对桩的变形影响要比对弯矩的影响大。因此,在确定土体的极限抗力时,除了比较实测和预测的荷载-最大弯矩关系,还应比较实测和预测的荷载-变形关系。
(5)在通过比较较大荷载水平下实测和预测的荷载-最大弯矩和荷载-变形关系准确确定极限抗力分布后,再通过比较整个荷载-变形关系可反分析得到Gs值。因此,采用弹塑性解答不仅可以确定土体的极限抗力,也可反分析土体的弹性变形参数。