5.4.3 黏性土中侧向受荷桩极限荷载的简化计算
(1)桩头自由长桩
在地面处桩基变形10%d时,最大弯矩发生深度平均值比塑性滑移深度值大0.17d;在地面处桩基变形20%d时,最大弯矩平均发生深度比塑性滑移深度小。因此,可假设最大正弯矩发生深度xmax(=npd)深度内土体抗力p全部达到极限抗力pu=NgSud1-n(x+α0)n。
当桩身最大正弯矩达到极限弯矩Mult时,在最大弯矩点处形成塑性铰,如图5-14所示。以最大弯矩点O为支点,计算得桩顶自由桩最大弯矩:
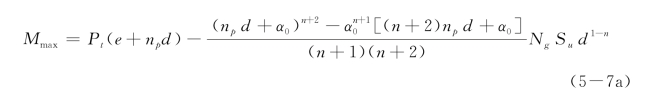
或
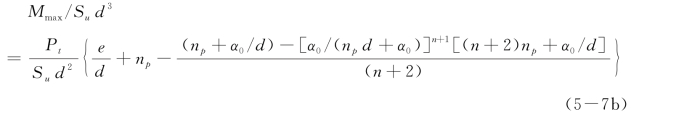
根据最大弯矩点O处剪力为零(即Pt与xmax深度内的土体总抗力相等),可得
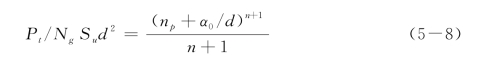
或
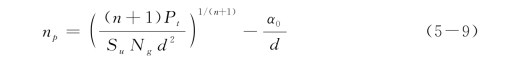
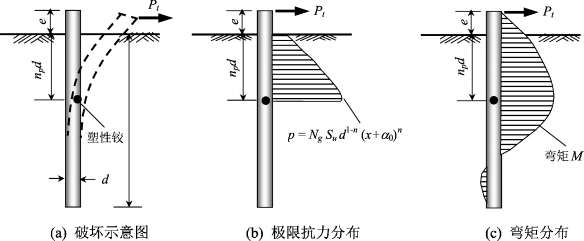
图5-14 黏土中桩头自由长桩极限荷载计算简图
如果以地面变形为10%d或20%d为设计标准,将np=3.24~6.76(平均值5.28)或4.27~8.06(平均值6.45)代入式(5-8)和式(5-7a),可得到相应的设计荷载和设计最大弯矩。对于上述数据库,采用地面变形为10%d或20%d对应的Pt和最大弯矩发生深度xmax,由式(5-7b)计算的Mmax/Sud3也列入表5-7。结果表明,由式(5-7b)得到的Mmax/Sud3与GASLFP理论计算的结果差别在4%以内。因此,在初步设计中,可根据桩材强度计算极限弯矩Mult或设计最大弯矩,然后由式(5-7a)和式(5-8)计算桩顶极限荷载Pult或设计荷载。
图5-15和图5-16分别给出了n=0.7,α0/d=0.2,e/d=0,Ng=0.5~3.5时,Pt/Sud2~np半对数以及Pt/Sud2~Mmax/Sud3双对数关系曲线。对于其他n,α0/d、e/d值对应的Pt(或Pult)/Sud2与np以及Mmax(或Mult/Sud3计算图表,可参见附录G。由图5-15和图5-16可见,Pt/Sud2和Mmax/Sud3随Ng值增加而增长,但增长速率随Ng值增加而降低。在Ng值较小时,Pt/Sud2和Mmax/Sud3变化比较显著;当Ng值大于2.5时,Pt/Sud2和Mmax/Sud3变化比较平缓。
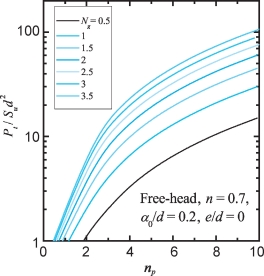
图5-15 桩头自由Pt/Sud2~np(e/d=0)
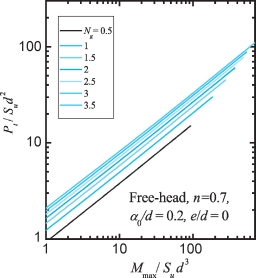
图5-16 桩头自由Pt/Sud2~Mmax/Sud3(e/d=0)
如果取α0=0 m和n=1.7,用γsd代替Su,式(5-7)和式(5-8)将分别退化成式(5-1)和式(5-2),即砂土的极限荷载和极限弯矩。如果取α0=0,n=1和Ng=3Kp,并用γsd代替Su,极限弯矩和极限侧向荷载有如下关系:
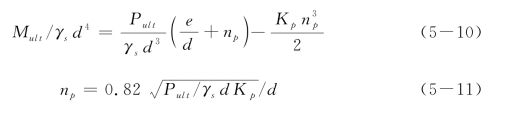
由发生极限弯矩点处剪力为零,可计算得Pult=1.5γsd Kp(npd)2,则式(5-10)可改写为
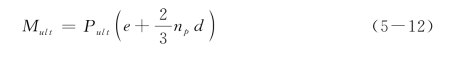
式(5-12)即为Broms(1964b)建议的砂土中桩头自由桩的极限荷载计算公式。
同样,如果取α0=0 m,n=0和Ng=9,并且将荷载作用高度视为e+1.5d(注:Broms假定1.5d深度内土体抗力为零),式(5-8)可简化Broms(1964a)建议的黏土中桩顶自由长桩的极限弯矩与极限侧向荷载关系式:
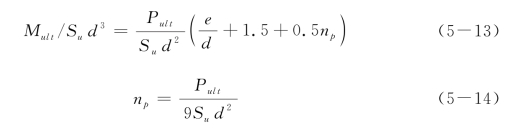
(2)桩头固定长桩
桩头固定长桩的破坏机理和计算如图5-17所示。当桩头负弯矩达到极限弯矩Mult和桩身最大正弯矩达到Mult时,分别在桩头和最大正弯矩处形成塑性铰。假设最大正弯矩发生深度为npd,在该深度内土体抗力p全部达到极限抗力pu=NgSud1-n(x+α0)n。以最大弯矩点O为支点,计算得桩顶自由长桩最大弯矩:
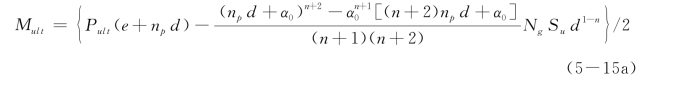
或
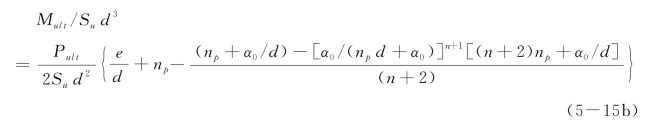
根据最大弯矩深度处剪力为零(即Pt与xmax深度内的土体总抗力相等),可得:
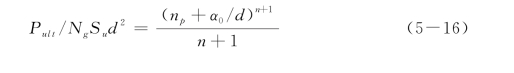
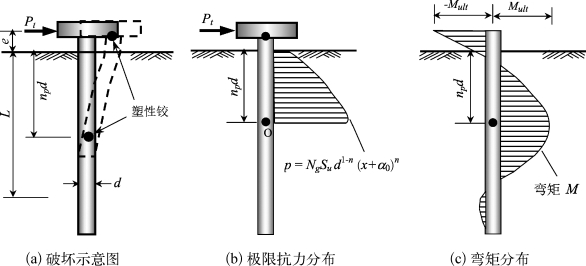
图5-17 黏土中桩头固定长桩极限荷载简化计算
或
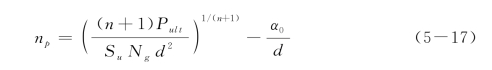
比较式(5-16)、式(5-17)和式(5-8)、式(5-9)可知:①如果Ng和Pult对桩头固定长桩和桩头自由长桩相等时,两者的最大正弯矩发生深度是相等的,前者的极限弯矩是后者的一半;②如果Ng和Mult在桩头固定或自由条件下相等时,前者的极限荷载Pult和最大正弯矩发生深度都比后者大。
图5-18和图5-19分别给出了n=0.7,α0/d=0.2,e/d=0,Ng=0.5~3.5时,Pt/Sud2~np半对数以及Pt/Sud2~Mmax/Sud3双对数关系曲线。对于其他n、α0/d、e/d值对应的Pult/Sud2与np以及Mult/Sud3计算图表,可参见附录H。与桩头自由条件相似,Pt/Sud2和Mmax/Sud3随Ng值增加而增长,但增长速率随Ng值增加而递减。在Ng值较小时,Pt/Sud2和Mmax/Sud3变化比较显著;当Ng值大于1.5K2p时,Pt/Sud2和Mmax/Sud3变化比较平缓。
如果已知Ng值和np值,由图5-18和图5-19可分别查得Pult/Sud2和Mult/Sud3。如取np=5.35(地面处桩基侧向位移为10%d时平均值)和Ng=1.0,可查图得:Pult/Sud2=16.4和Mult/Sud3=24.4。反之,如果已知Ng值和桩的设计最大弯矩Mult值,则可直接查图得Pult/Sud2和np值,从而得到极限荷载Pult。
与桩顶自由长桩的讨论相似,通过选取相应的α0、n和Ng值,式(5-15)和式(5-16)可简化为砂土中桩头固定长桩以及黏土中桩头固定长桩由Broms(1964b)建议的极限荷载和极限弯矩关系公式。这里不再赘述。
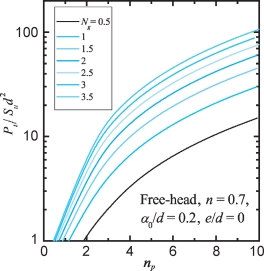
图5-18 桩头固定Pt/Sud2~np(e/d=0)
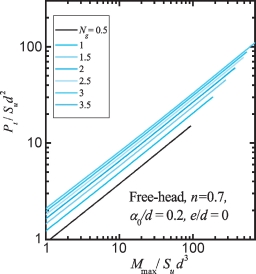
图5-19 桩头固定Pt/Sud2~Mmax/Sud3(e/d=0)
