6.5.2 实例CN2
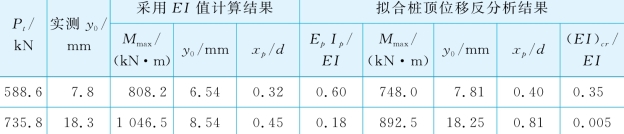
桩E的嵌入长度9.5 m,桩径1.2 m。原文报道的桩截面抗弯刚度可能有误,因为由EI=115.28 MN·m2(Nakai& Kishida,1982)得等效杨氏模量Ep=1.13×106kPa,远小于混凝土的杨氏模量。因此,本文取Ep值为一般混凝土的模量,即Ep=2.5×107kPa,即有E I=2.54 GN·m2和fc′≈(Ep/151 000)2≈27.5 MPa。采用ACI kr值,根据式(6-2)计算得开裂弯矩为554.2~886.7 kN·m(其中,混凝土边缘距中性轴距离zt=d/2=0.6 m),该下限值与Nakai&Kishida(1982)报道的开裂弯矩527.6 kN·m非常接近。由于缺少钢筋配置资料,不能直接采用程序MUEI计算极限弯矩和由式(6-5)计算EpIp值,因此,采用与实例CN1相同的过程,根据实测桩顶位移资料反算 。
。
如图6-26所示,桩E试验场地由多层土体组成,在上部10d范围内,主要为黏性土。在地面下2 m范围内,NSPT为零,在2~10 m之间,NSPT约为4~6。在地面下3 m附近,黏性土的不排水强度Su≈163.5 kPa。根据Kishida&Nakai(1977)建议值,取Gs=130.8Su=21.38 MPa。荷载作用在地面上0.35 m。
参照第5章的分析,取n=0.7,Ng=2和α0=0.06(由于Su值比到地面附近土体强度大,取较小值)。在5d深度内,该LFP与c=8 kPa和φ=10°的Hansen LFP非常接近,小于Matlock LFP(图6-31)。采用E I值和程序GASLFP计算得桩顶侧向变形如图6-32中虚线所示。在Pt小于约470 kN时,计算值与实测桩顶变形比较吻合较好;当Pt大于470 kN后,实测桩顶变形逐渐偏离计算值。因此,可取Pcr=470 kN,相应的M cr=628.4 kN·m和kr=22.3。
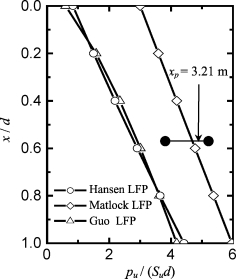
图6-31 桩E的LFP
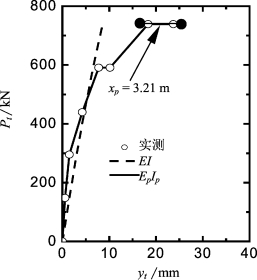
图6-32 桩E的Pt-yt关系
采用上述Gs和LFP以及程序GASLFP,通过拟合Pt=588.6 kN和735.8 kN对应的计算桩顶位移和实测值(初始值,即不考虑时间效应),反分析得到EpIp/EI值分别为0.6和0.18(表6-13)。由采用EI计算的Mmax,根据式(6-5)可反分析得:Pt=588.6 kN和735.8 kN对应的(EI)cr/EI值,如表6-13。Pt=735.8 kN对应的(EI)cr/EI值远比P t=588.6 kN对应的值小,因此桩在Pt=735.8 kN时可能已经发生了破坏。从Nakai& Kishida(1982)没有报道该荷载水平下的弯矩分布,也可能证实了这一点。其他荷载水平下的实测和计算弯矩比较相当吻合,如图6-33所示。
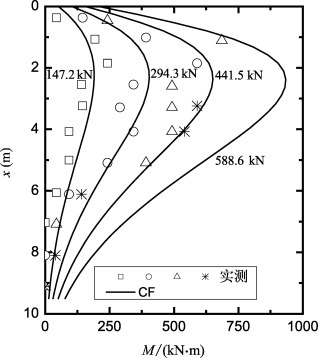
图6-33 桩E的实测和计算弯矩比较
表6-13 桩E非线性性状的预测