2.4.1　基于结构动力修改技术的工件动力学演化分析

2.4.1　基于结构动力修改技术的工件动力学演化分析

采用结构动力修改技术可以快速、有效地预测工艺系统的动力学特性演化情况［11］。在薄壁零件的切削过程中，工件系统的模态参数会随着加工余量的不断切除而连续变化［2］。

工艺系统的动力学方程可以表示为

式中：M为工艺系统的模态质量矩阵；C为工艺系统的模态阻尼矩阵；K为工艺系统的模态刚度矩阵；u（t）为位移向量；F（t）为切削力向量。

当切削力为激振频率为ω的谐波力时，其相应的系统位移为

式中：A为工艺系统的动柔度矩阵。

根据结构动力修改理论，结构修改部分即切除材料的动力学矩阵为

式中：ΔM为结构修改部分的模态质量矩阵；ΔC为结构修改部分的模态阻尼矩阵；ΔK为结构修改部分的模态刚度矩阵。

结构动力修改之后，工艺系统的动柔度矩阵为

因此，结构动力修改前与修改后工艺系统的动柔度矩阵具有如下关系：

对式（2.20）进行变换，可以得到

其中，I为单位矩阵。

以航空发动机薄壁环形机匣为例，机匣切削过程中由材料切除引起的工艺系统动力学特性变化，可以看作工艺系统局部的结构动力修改，即

将式（2.22）代入式（2.21），可以得到

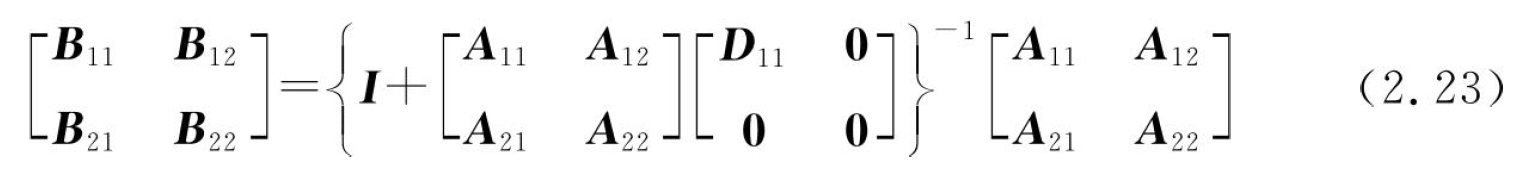
上述的结构动力修改求解过程，没有考虑工艺系统自由度的增减问题，这对于薄壁零件的半精、精加工过程是可行的。因为材料切除单元的体积很小，特别是在机匣外型面法向上的结构变化不太明显。但对于这类零件的粗加工，如果不考虑工艺系统自由度的增减问题，会造成预测精度严重下降。

由式（2.23）可知，知道了工艺系统初始的模态参数和结构修改部分的模态参数，便可计算得到工艺系统结构修改之后的模态参数。其中，工艺系统初始及结构修改部分的模态参数可以通过有限元方法进行计算。