2.4.2 基于薄壳模型的工件动力学演化分析
2.4.2.1 常见壳体结构的双曲薄壳力学模型
在航空航天装备结构中,壳体结构非常常见。这些壳体的几何特征一定程度上可简化表征为球面、双曲抛物面、圆柱面和其他复杂形状,如图2.18所示。曲面单元能够更好地模拟真实结构,得到的计算结果会更有效。但是,曲面壳体的变形与平板变形有所区别。对于曲面单元,现常采用考虑横向剪切变形的曲面壳单元。从图2.18中可以得知,壳体结构一般在一个或两个方向上有不同或相同的半径,此外还存在某个方向的扭曲。相比平板,双曲薄壳近似结果更精确,因此引入双曲薄壳对常见壳体进行近似表示[12]。本书以双曲薄壳为对象进行介绍。
考虑一个双曲浅壳,其中曲面在正交绝对坐标系统(ACS)中可表示为如下方程:

式中:Rx和Ry是x和y方向上的曲率半径;Rxy为曲面的扭曲半径,表示曲面的扭曲程度。
为分析方便起见,通常限定Rx、Ry和Rxy为常量,在这种情况下,式(2.24)表示一个二次曲面,如图2.18(a)所示;当Ry=R且Rx=Rxy=∞时,式(2.24)表示圆柱面,如图2.18(b)所示;当Rx=Ry=R且Rxy=∞时,式(2.24)表示球面,如图2.18(c)所示;当Rx=-Ry=R且Rxy=∞时,式(2.24)表示双曲抛物面,如图2.18(d)所示。壳体的中性面是一个曲面,壳单元受力状态及应力状态如图2.19所示。假设壳的中曲面满足基尔霍夫假设,中曲面的应变ε0、扭转应变γ0以及曲率变化κ可以表示为
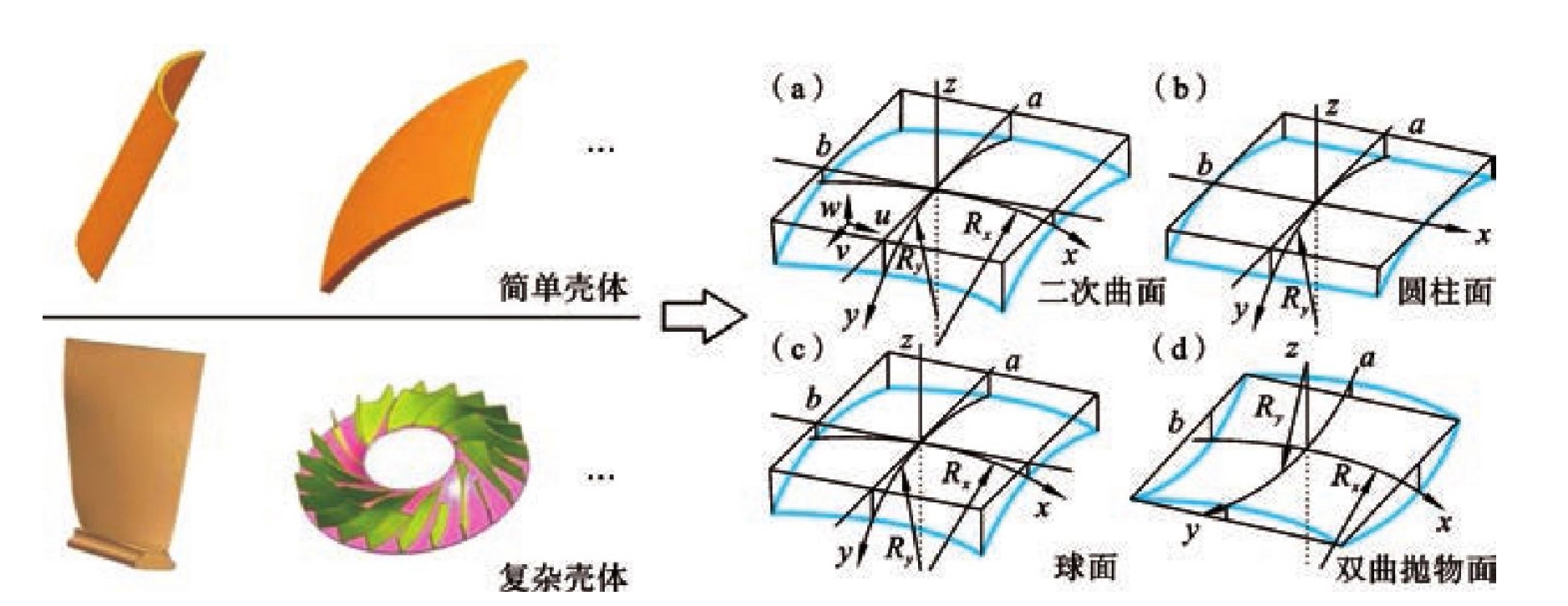
图2.18 常见的壳体结构
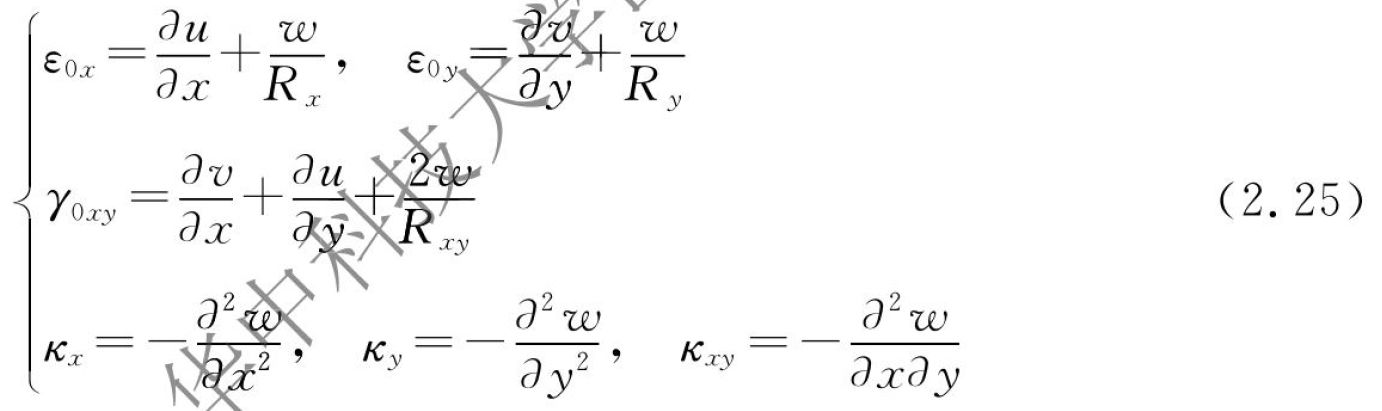
式中:u、v和w为中曲面在x、y和z方向的位移。壳体中任一点的应变ε和扭转应变γ表示为
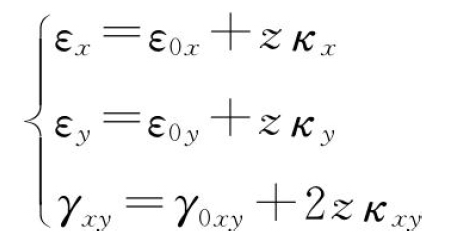
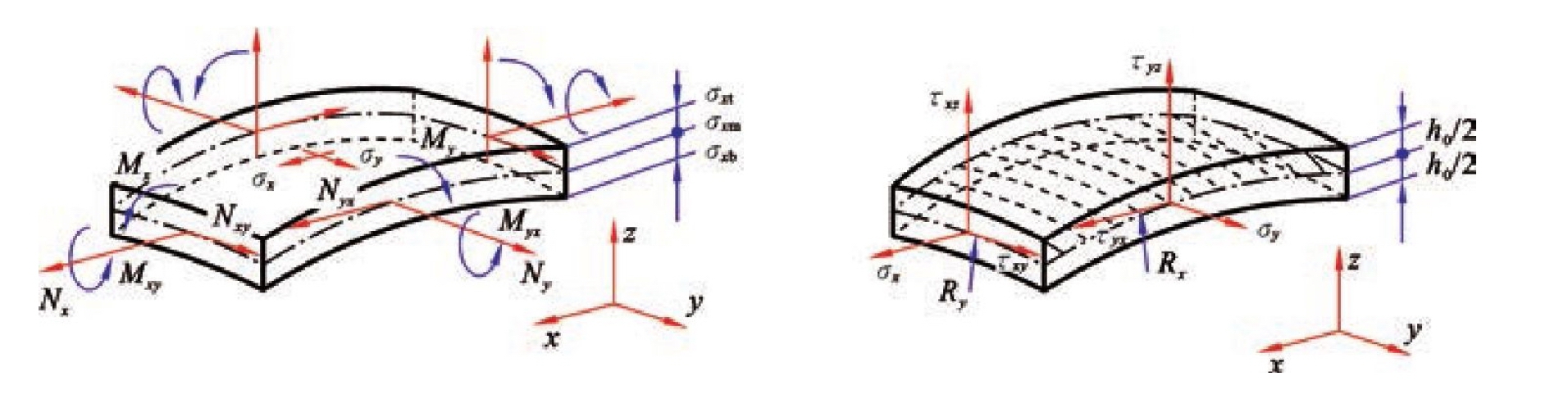
图2.19 壳单元受力状态及应力状态
在壳体上取一个微小单元进行分析,单位长度上的合力Nx、Ny和Nxy与中曲面相切。单位长度上的合力矩为Mx、My和Mxy,如图2.19所示,考虑横向剪切力的力平衡方程可得到运动方程:
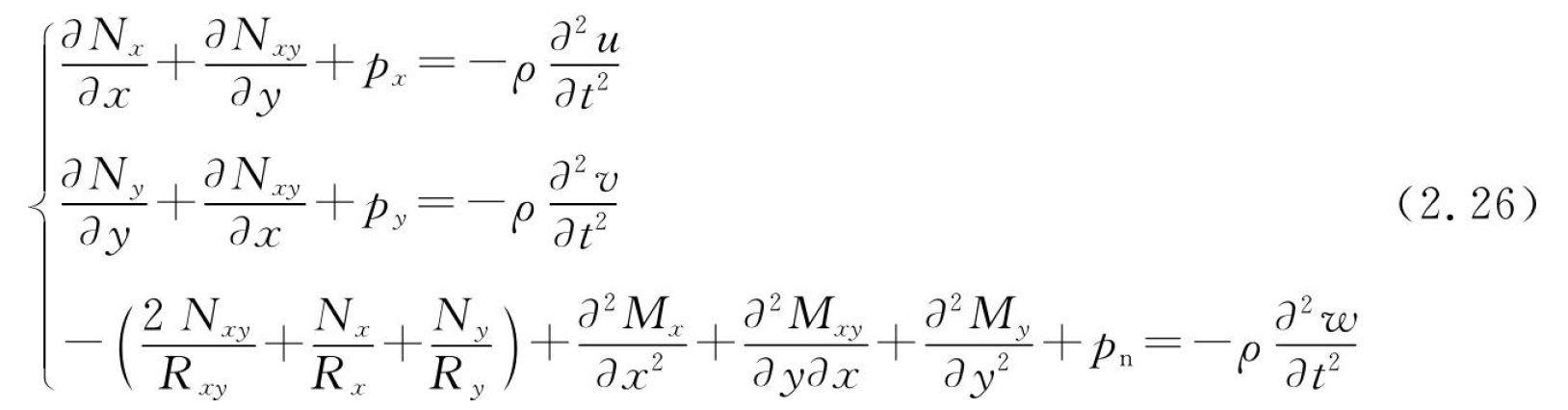
式中:px、py是外部作用力在切向方向的分力;pn是法向方向的分力;ρ为材料密度。对于各向同性的壳体材料,应变与应力的关系为
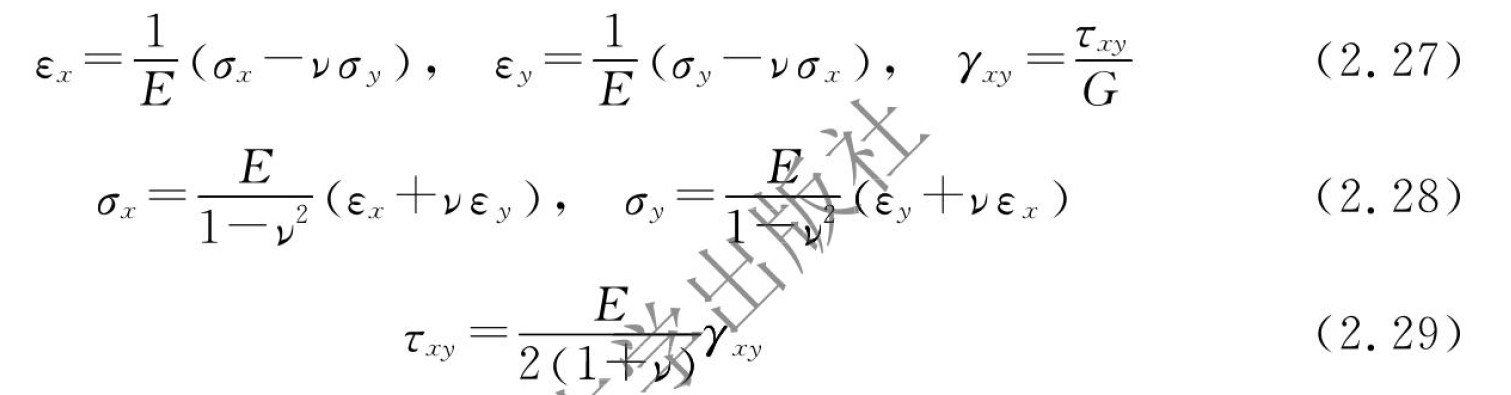
式中:σ为应力;τ为扭转应力;E为弹性模量(杨氏模量),ν为泊松比,G为剪切模量,三者满足G=E/[2(1+ν)]。在截面上对应力进行积分可以求出合力,在厚度h0上对应力进行积分可以得到弯矩,即
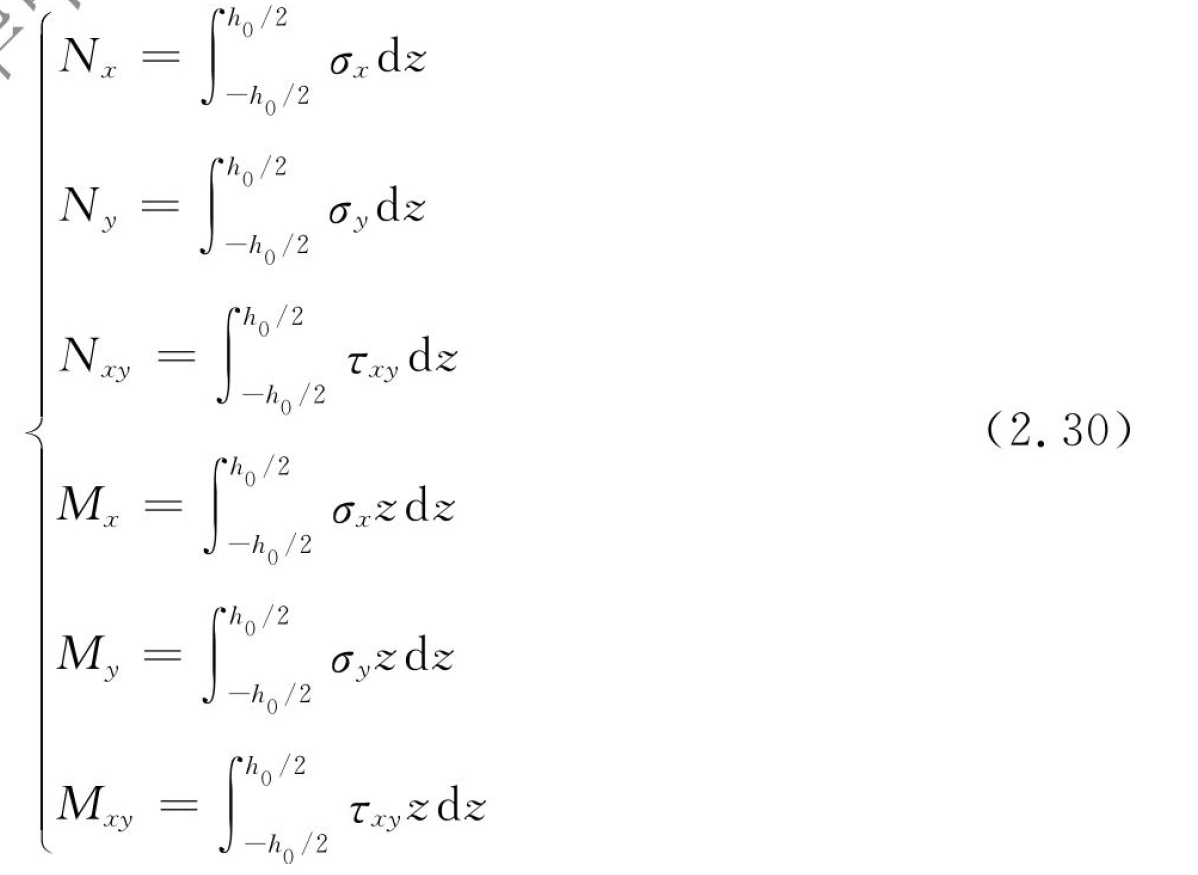
合力矩表示为

式中:
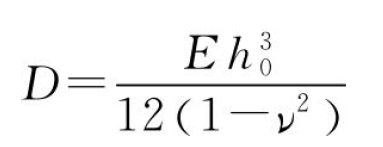
其中,D为壳体的抗弯刚度。在正交坐标系下,浅壳的运动方程用位移矩阵表示为
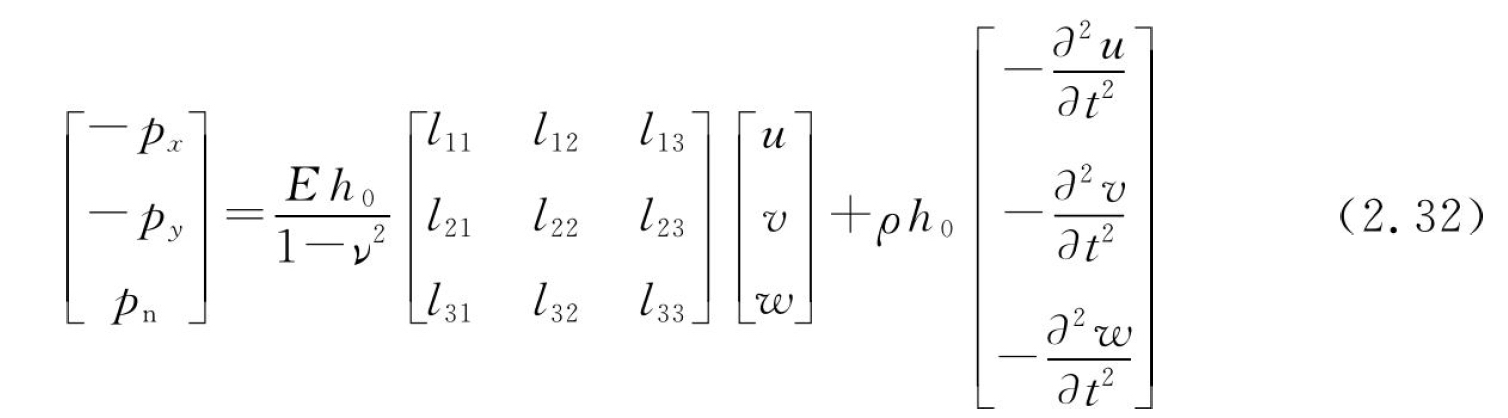
其中,lij(i,j=1,2,3)为微分算子。
根据经典的里兹能量法,壳体中的势能是由应变能产生的,表示为
式中:PEs由中间曲面受拉伸产生,PEb由弯曲产生[13],且
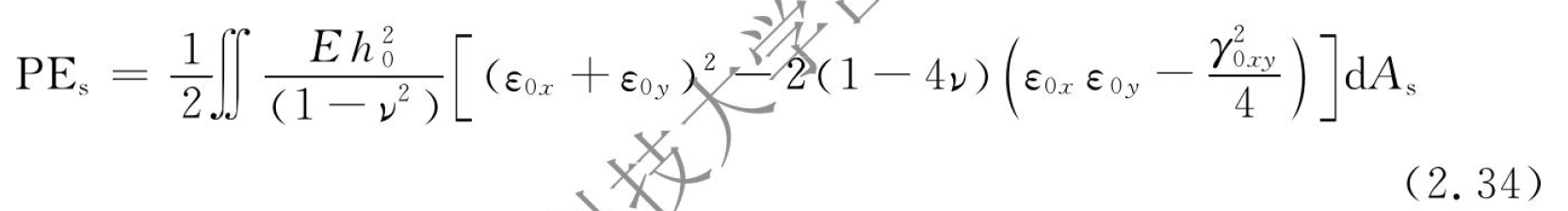
式中:As为壳体的中曲面的面积。
在壳体中,弯曲产生的势能为
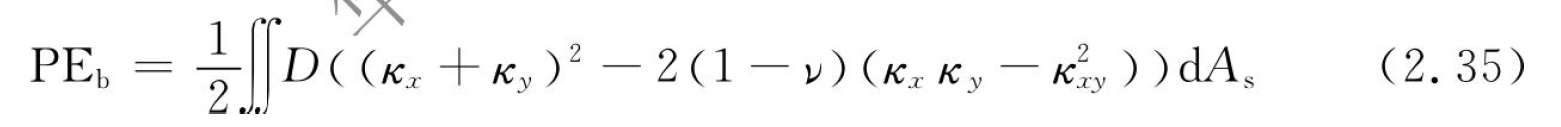
振动的动能为
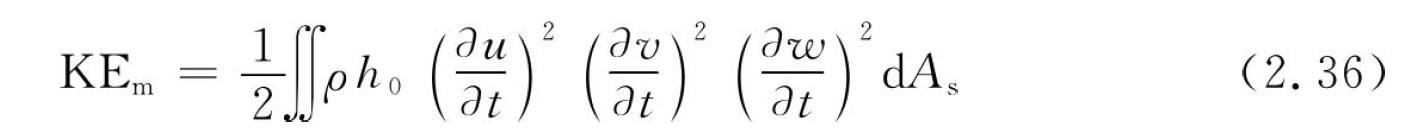
在式(2.34)至式(2.36)中,能量表达式是由包含杨氏模量E、材料密度ρ、壳体厚度h0的函数积分得到的,因此上述动能和势能的求解方法适用于变厚度或非均质材料的壳体。
对于底面固定装夹的壳体,其边界需满足在边界处x向位移为零,y向位移为零,z向位移为零,以及z向速度为零,即满足式(2.37)至式(2.41):
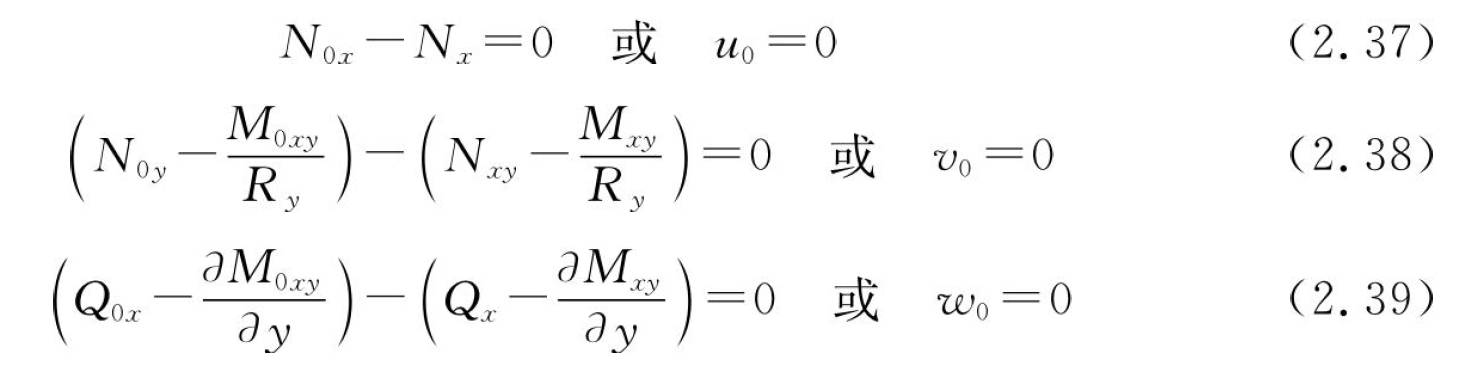
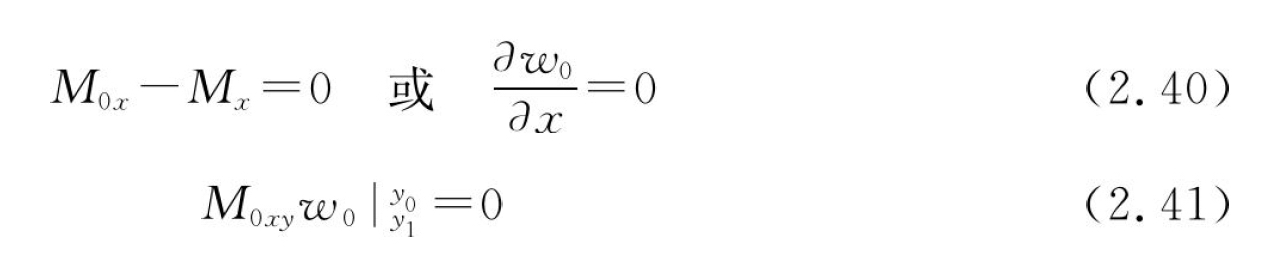
2.4.2.2 不同切削加工方案下的切削厚度建模
在浅壳的加工过程中,若采用不同的加工方案,其中间加工阶段的零件形状会不同,但是最主要的差别是切削厚度的变化不同。一般情况下主要存在三种加工方案:单向切削、往复切削、环绕式切削。
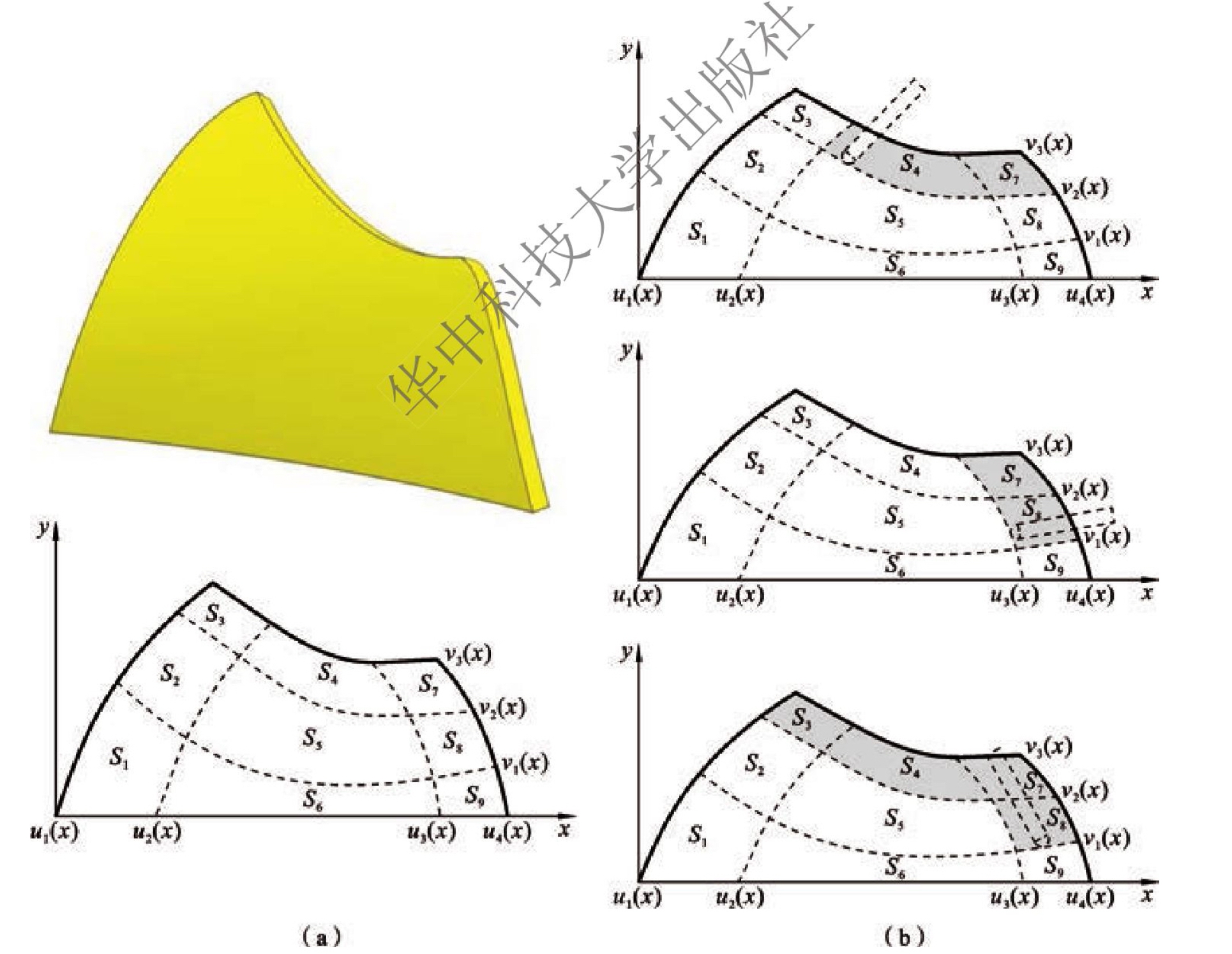
图2.20 典型的壳体结构及其在Oxy平面上的投影和切除顺序
(a)典型结构在Oxy平面上的投影(b)典型切削顺序
把浅壳投影到Oxy平面,会形成一个封闭区域。为了使分析简单,x轴和y轴被重新定义在一个不同的正交绝对坐标系,如图2.20所示。为了模拟切削过程,将浅壳的投影区域分为九个子区域。从左至右,边界曲线和分割曲线分别由u1(x)、u2(x)、u3(x)、u4(x)表示。由下往上,边界曲线和分割曲线由v1(x)、v2(x)、v3(x)依次表示。九个子区域分别标记为S1、S2、S3、S4、S5、S6、S7、S8、S9。每个子区域的厚度是H1、H2、H3、H4、H5、H6、H7、H8、H9。采用上述的参数化模型,可以调整相应的分段光滑曲线与每个区域的厚度来模拟切削加工过程。图2.20(b)中列出了一些在切削加工过程中可能的情况,其中灰色区域表示已加工区域,其厚度发生了变化。
2.4.2.3 模态频率与模态振型求解
本书使用瑞利-里兹法求解薄壳在加工过程中任一阶段的固有频率和模态振型。薄壳的振动方程假设为满足悬臂边界约束条件的正弦函数,可以用如下方程表示:
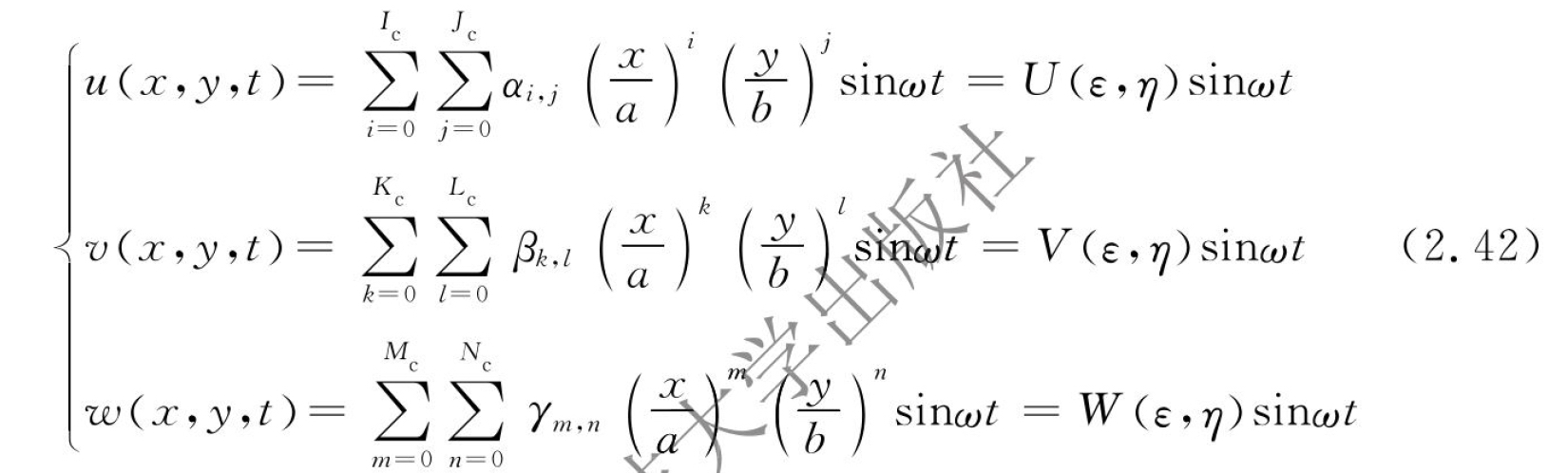
式中:a和b表示壳体相应的水平宽度和垂直高度;ε和η是对应x和y的无量纲坐标,即ε=x/a,η=y/b;Ic、Jc、Kc、Lc、Mc和Nc表示正整数。
为了求解自由振动问题,根据里兹能量法,将位移方程代入能量方程式(2.33)并将壳体的总势能相对于系数αi,j、βk,l和γm,n最小化,可以获得下面的方程式:
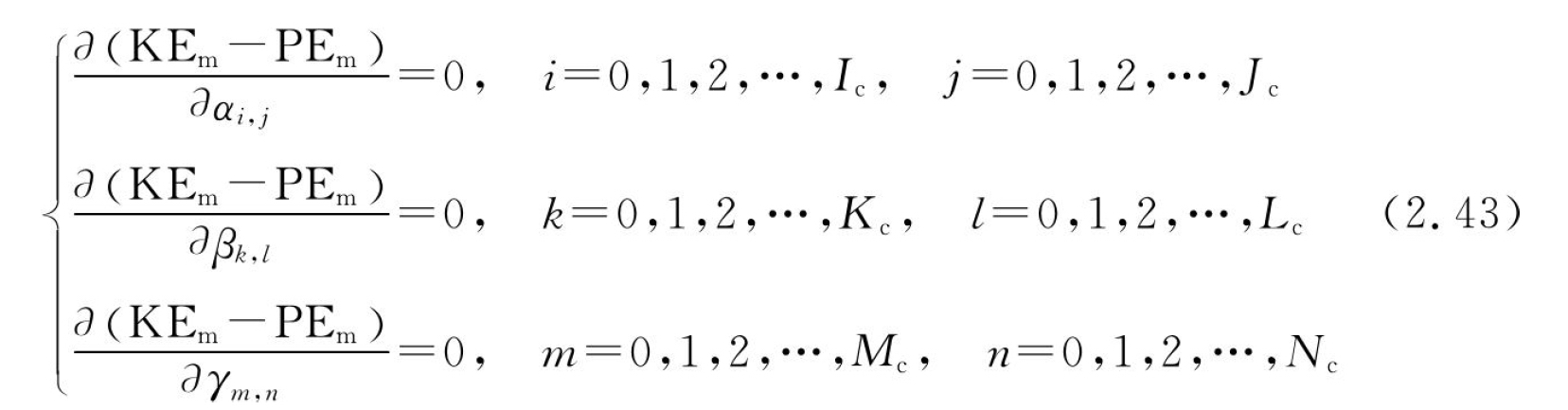
可通过求解相应方程式获得特征值。然后,将特征值代入方程式(2.43)可以计算出相应的特征向量。最后,将特征向量代入方程式(2.42),能够得到对应于各频率的模态振型。
由以上分析可知,解析方法的复杂程度取决于模型复杂度。当壳体的轮廓形状或加工过程的中间阶段的几何形状十分复杂的时候,解析方法的计算量异常大,几乎不可能实现。因此通常需要将模型简化,例如将边界曲线近似为直线或只分析特定的几个中间阶段。
