本章参考文献
第6章 薄壁零件加工残余应力变形的装夹感知
薄壁零件在实际应用中,需要很精确的装配定位基准,这就意味着要求很高的制造精度。数控加工是航空薄壁零件的主要制造技术,是决定加工质量和效率的关键因素之一。薄壁零件结构复杂,壁薄,自身刚度弱且分布不均匀,加工难度非常大。数控加工过程中切削力热载荷、装夹力载荷以及残余应力载荷等作用在工件上,导致工件发生变形,影响加工精度的控制和加工效率的提升。目前生产中采用的解决措施是使用保守的切削参数,并在加工完成之后进行二次补偿加工或者手工校形等。这都造成了生产质量和效率的降低。
数控切削加工引入的残余应力变形,是造成零件超差报废的重要原因。切削加工金属材料时,毛坯材料的初始残余应力状态被打破;同时加工过程中工件与刀具相接触部分的材料发生塑性变形,在工件加工表面下的薄层内,产生了相当大的加工残余应力。由于薄壁零件具有壁薄、刚性弱等特性,装夹释放后,极易发生残余应力回弹变形,导致零件整体变形超差。如何预测与评估薄壁零件数控加工导致的残余应力变形并对其进行工艺优化控制,是目前研究的热点问题,也是我国航空复杂薄壁零件加工质量提升面临的巨大挑战[1,2]。
6.1 切削加工中的残余应力
金属的切削过程实质上是一个金属发生挤压变形并最终屈服断裂的过程。金属受到挤压时,其内部在生成主应力的同时,还会在与挤压方向成45°角的方向产生最大剪应力,在剪应力达到金属材料的屈服极限时,材料就会屈服并产生剪切滑移,最终断裂。金属的切削加工过程可以看作刀具对工件材料的周期挤压过程,刀具不断挤压工件材料并使其沿最大剪应力方向滑移断裂从而实现材料去除。
图6.1所示为切削过程与残余应力生成机理。在切削加工时,刀尖圆弧前端的工件材料会沿两个方向流动。O点以上的材料,会从前刀面流出最终形成切屑,O点以下的部分,会受到加工刀具的挤压,留在已加工表面上,形成加工表层。留在加工表面上的这层材料的塑性变形是残余应力产生的主要原因。在刀具圆弧前端,工件材料受到刀具的切削剪切力的作用,材料晶粒沿切削方向会出现塑性收缩,而垂直于切削方向会发生塑性拉伸。这种现象称作“塑性凸出效应”,塑性凸出效应会使加工表面产生残余拉应力。随着刀具的继续切削,已加工表层材料会受到刀具后刀面的犁耕力与摩擦力的作用,刀具对表层材料产生挤压与摩擦,表层材料会进一步发生变形,这种现象称作“挤光效应”。挤光效应往往在已加工表面形成残余压应力。这两种效应主要是由切削力的作用产生的,统称为机械效应。
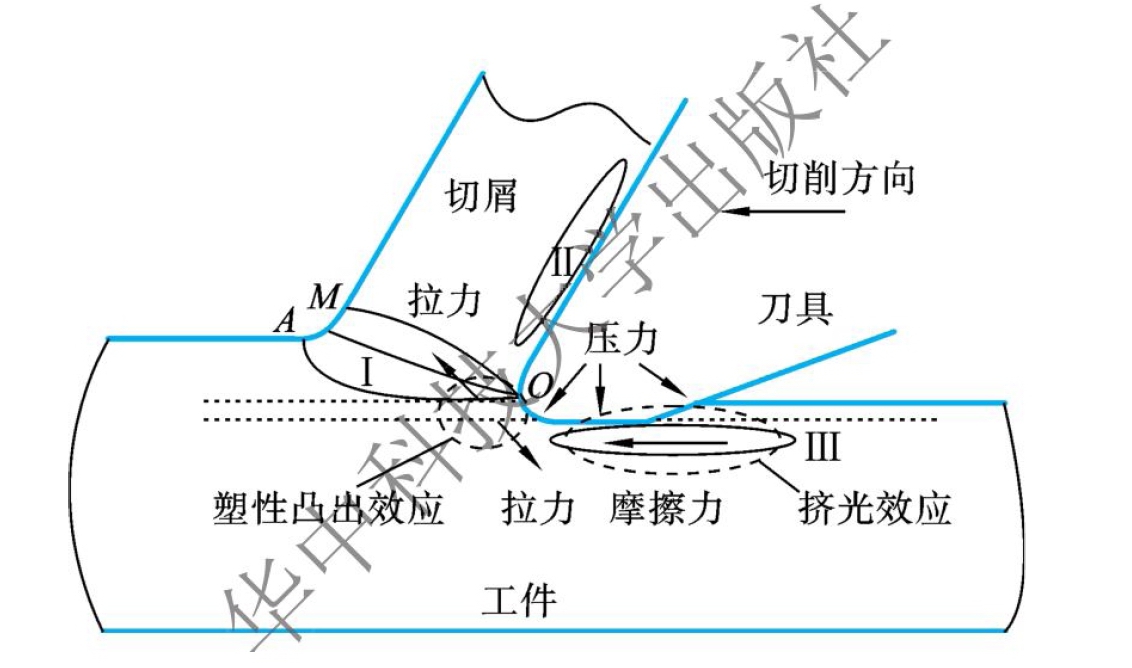
图6.1 切削过程与残余应力生成机理
金属切削加工过程中,刀具-工件接触界面上会出现剧烈的剪切、挤压、摩擦以及材料屈服流动现象,切削力做功会产生大量的切削热,刀具-工件接触区域的温度会逐渐升高。正常的切削加工中,切削区域的温度可达几百摄氏度,切削温度场存在着非常大的变化梯度。由于大温度梯度的存在,从工件表面到工件内部,温度急剧下降,切削时工件表层材料受热会发生热膨胀,产生拉伸变形,但同时表层材料又受到内部未变形材料的约束,这造成材料受压。在切削过程完成后,工件表层和内部材料的温度都会下降到室温,此时工件材料发生收缩,工件表层收缩多,内部收缩少,表层材料的收缩受到里层材料的约束,最后工件表层出现残余拉应力,里层出现残余压应力。因此,加工表面的温度场幅值越高、温度梯度越大,工件表层的残余拉应力越大。由工件内部切削温度分布不均导致的影响统称为热效应。
切削加工过程中,热效应与机械效应同时产生,在工件表层产生了相应的热应力与机械应力,两者叠加决定了切削完成后工件表层的残余应力分布状态。也就是说,热力耦合效应是切削完成后工件表层的残余应力分布的决定性因素。切削导致的工件表层残余应力分布表征为
式中:σT为切削导致的工件表层的残余应力;σMech为机械效应引入的残余应力;σTherm为热效应引入的残余应力。
铣削表层残余应力分布是由接触界面上的热力耦合效应导致的,而切削过程的热力耦合状态与切削工况密切相关。根据工件表面切削工况的不同,工件表层残余应力将会呈现不同的分布形式。
6.2 残余应力变形
根据变形机理的不同,薄壁零件的残余应力变形可以分为两种:初始残余应力变形和加工残余应力变形。一方面,毛坯材料生产制造过程中不可避免地会引入初始残余应力。虽然航空用零件毛坯大多经过了去应力处理工序,但是初始残余应力不可能完全消除,经过去应力处理后,毛坯的残余应力大多在几十兆帕左右。加工过程中,特别是粗加工过程中,材料被大量去除,毛坯的内应力平衡状态被打破,造成内应力重分布与再平衡。在此过程中,应力再平衡产生了应变,便产生了初始残余应力变形。另一方面,材料去除时,在刀具-工件接触界面上存在强烈的热力耦合作用,工件表层产生塑性变形,在热力载荷卸载后无法恢复,造成已加工区域表层存在很大的加工残余应力。这个应力在表层沿深度方向变化梯度很大,作用范围在表层几百微米以内。加工残余应力的引入产生了等效力矩,使工件发生加工残余应力变形。一般情况下,两种变形形式共同作用,决定了最终零件的变形状态。当工件壁厚较大时,工件刚度较大,由于加工残余应力作用层很薄,因此,其对零件的变形量贡献较小。但是在薄壁零件加工中,零件最终的厚度可能达到1 mm以下,工件刚度很小,这时加工残余应力作用层已经占了整个工件厚度相当大的比例,此时加工残余应力变形作用非常显著。
如图6.2所示,假设毛坯初始状态为应力平衡状态,零件未发生变形,如图6.2中的a状态。初始残余应力变形是由毛坯材料被切除造成的,这就相当于材料的去除导致部分应力弹簧(残余应力)的去除,零件内应力平衡状态发生改变,零件发生变形恢复平衡状态,造成了零件的初始残余应力变形,如图6.2中的b状态。相应的,切削加工会在工件表层引入加工残余应力,这就相当于在原工件系统上添加了应力弹簧,同样会造成内应力的失衡,引起工件变形,如图6.2中的c状态,这就是加工残余应力变形。
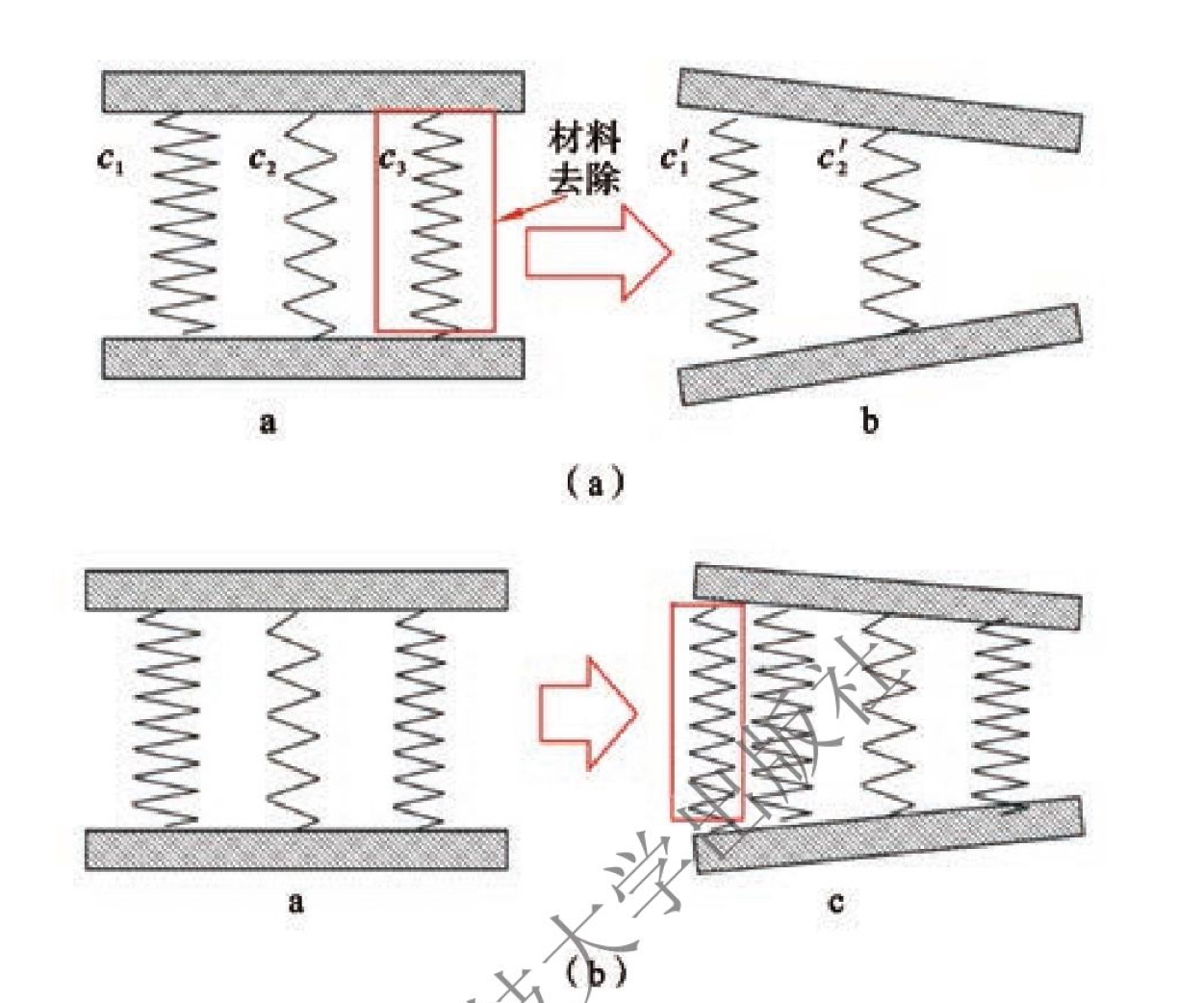
图6.2 残余应力变形的弹簧模型
(a)初始残余应力变形(b)加工残余应力变形
在零件的整个加工过程中,这两种残余应力变形同时存在,根据变形叠加原理,两者叠加表现为最终的零件残余应力变形。根据这两种变形的生成机理,可将加工过程分为粗加工过程和半精、精加工过程两个工序阶段来进行分析。如图6.3所示,对于航空发动机难加工材料薄壁零件,粗加工阶段,零件厚度比较大、刚度较大,毛坯材料被大量去除,初始残余应力变形程度与材料去除量密切相关,此时零件初始残余应力变形较大,占据绝对主导地位,可近似认为初始残余应力变形就是此过程的残余应力变形。半精、精加工阶段,特别是对精密薄壁结构件制造而言,零件多经过了去应力和校形工序,粗加工阶段的变形较少引入后续工序或在后续工序中被切除。在零件的半精、精加工阶段,材料去除量较小,此时零件将被加工至最终的零件厚度,壁厚很小,此时对变形起主要作用的是切削引入的表层残余应力,加工残余应力变形将起主导作用。
根据材料力学原理,在加工零件上建立直角坐标系,则其内部任一点的内应力可表示为如下的张量形式[3]:
图6.3 各工序阶段残余应力变形分析
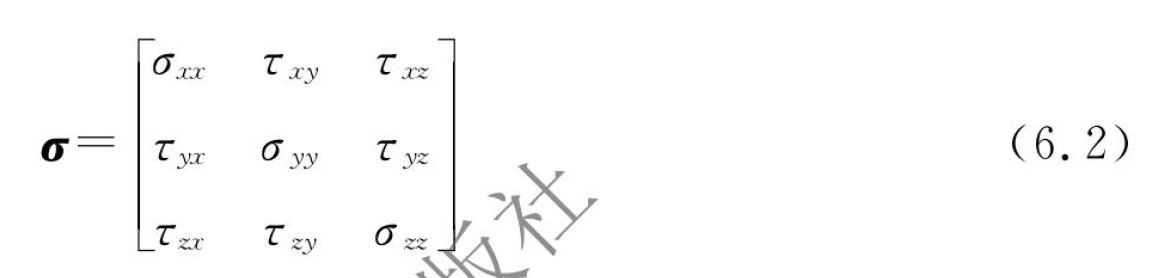
式中:σxx、σyy、σzz为正应力分量;τxy、τyx、τxz、τzx、τyz、τzy为剪应力分量。
正应力分量与剪应力分量共同构成了一点的应力状态,正应力的不平衡将导致零件的弯曲,剪应力的不平衡将导致零件的剪切扭曲。三个正应力分量中,σzz为厚度方向的正应力,对薄壁零件而言,厚度方向的抗弯刚度最大,σzz对变形的贡献非常小。另外实际生产中,采用的毛坯多为预拉伸板材或者轧制板材,且经过了去应力处理,剪应力分量非常小。因此,在目前的研究中,研究者多忽略厚度方向的正应力和剪应力分量对薄壁零件加工变形的影响,重点分析目前可以有效测量的σxx、σyy两个正应力分量。σxx和σyy为平面应力,分别对应零件沿XX方向和YY方向的弯曲变形。基于以上原因,对于初始残余应力场,可重点分析零件长宽方向的正应力对初始残余应力变形的影响;对于加工残余应力场,可重点分析刀具切削进给方向和垂直进给方向上的正应力对加工残余应力变形的影响。
6.3 残余应力变形感知预测原理
目前的初始残余应力场测量手段是对毛坯进行切片离散进而获取应力状态,测量中存在着均匀性的假设。实际加工中,对于一些复杂形状的零件毛坯,在其制造过程中由于毛坯边界的复杂性,生成的初始残余应力场分布不均,毛坯初始残余应力场的复杂性使得测量均匀性假设不成立,从而初始残余应力场难以准确测量。这使得零件毛坯初始残余应力状态难以准确获取,从而基于应力场的残余应力变形预测方法不适用。另外,铣削加工过程中,工况因素对加工质量有着重要的影响,会直接决定最终的表层加工残余应力状态,从而影响加工残余应力变形的生成。已有的加工残余应力变形预测方法是基于工况映射和应力贴合实现的,要求加工过程可以离散为定常工况。但是针对时变工况加工过程,加工残余应力场在工件表层分布不均匀,难以通过测量的手段对表层应力场进行评估。基于变形势能感知的残余应力变形预测方法就是针对这一问题提出的。所谓残余应力变形的感知预测,就是在实际的加工过程中,通过传感器对因引入残余应力而产生变化的可监测量进行监测,获得加工前后监测量的变化。在此基础上,对装夹状态下工件的残余变形势能进行感知,建立监测量与最终残余应力变形之间的映射关系,预测零件装夹卸载后自由状态下的残余应力变形。其原理如图6.4所示。
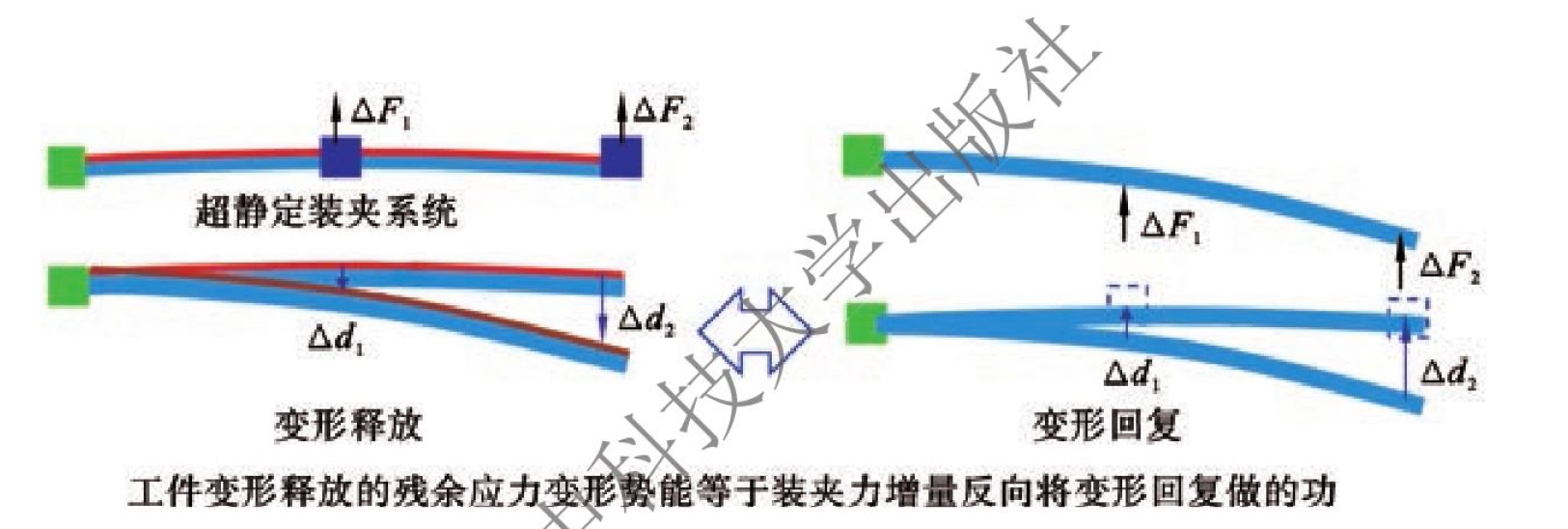
图6.4 残余应力变形势能感知原理
下面从能量的角度对残余应力变形的感知预测原理进行说明。材料去除在工件内部引入了附加应力场,这个附加应力场由初始残余应力场再平衡引入的附加应力场及热力耦合导致的加工残余应力场两部分组成。假设该附加应力场已知,且只考虑正应力作用,那么其在工件内部引入的总能量可以表示为
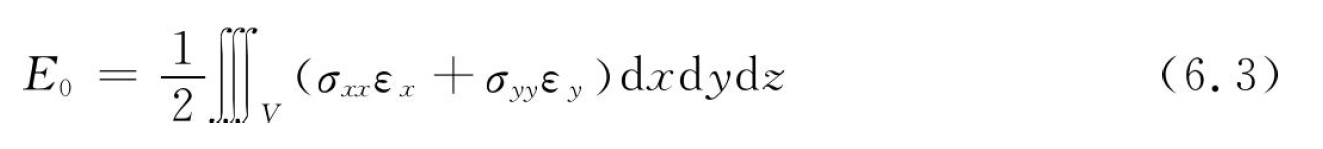
式中:E0为切削引入的能量;σxx和σyy为应力;εx和εy为应变。
装夹释放后,在残余应力等效力矩作用下工件产生残余应力变形。定义变形后工件内残余的能量为E1,E1为此时零件内部的势能。残余应力变形做功满足最小势能原理,即达到平衡状态时,在满足给定边界的位移场中,真实的位移场使得工件的势能最小[4],即

定义Ed为装夹释放后非平衡残余应力做功导致工件变形所释放的能量,可以表示为
由于装夹的限制,残余应力变形在装夹状态下不表现,能量以势能的方式存储在工件中。装夹卸载后,这部分势能做功表现为残余应力回弹变形,即回弹变形所释放的势能为残余应力变形势能。在装夹状态下,这部分能量的存在导致装夹力发生变化,装夹应力场平衡了切削造成的附加应力场。如图6.4所示,根据虚功原理,装夹点释放后,工件发生残余应力变形,工件释放的残余应力变形势能与装夹力增量反向将变形回复所做的功相等。同时工件装夹点的位移也可以近似表示为装夹力变化值的函数,即
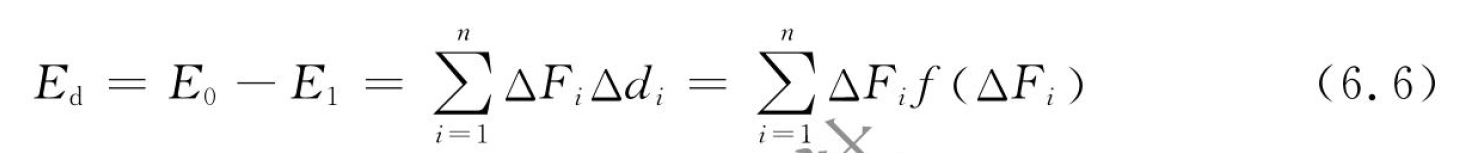
式中:ΔFi为第i个装夹位置的装夹力变化值;Δdi为第i个装夹位置释放后的变形。
根据式(6.6),装夹力的变化与残余应力变形势能存在映射关系,通过监测工件装夹力的变化即可评估整体的残余变形势能,进而达到预测零件的残余应力变形的目的。
6.4 残余应力变形感知预测模型
为了实现残余应力变形的感知预测,需要建立相应的数学模型。记D为感知目标矩阵(预测的零件残余应力变形),ΔF为感知量矩阵(装夹力的变化值),f为感知量矩阵到目标矩阵的映射关系,则残余应力变形感知预测模型的一般化表达式可以表示为
式中,各量分别为
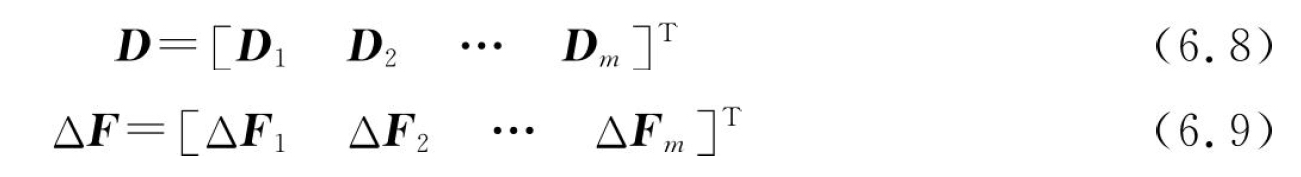
感知量矩阵ΔF代表不同感知时刻(1,2,…,m)不同感知位置(1,2,…,n)装夹力变化值。定义初始装夹力为F0=[F01 F02 … F0n],向量中各元素代表初始时刻0感知位置(1,2,…,n)的装夹力,各个元素的数值需要通过压力传感器感知来确定。零件的加工过程相当于给残余应力变形感知系统提供激励,引入残余应力变形势能,使装夹力发生变化,定义时刻1的装夹力为F1=[F11 F12 … F1n],则装夹力变化向量ΔF1=F1-F0。随着切削过程的进行,新的感知时刻不断取定,在新的时刻感知到的装夹力分别为F2,F3,…,Fm,对应扩展的装夹力变化向量分别为ΔF2,ΔF3,…,ΔFm。
目标矩阵D代表不同感知时刻(1,2,…,m)不同感知位置(1,2,…,k)零件残余应力变形矩阵。目标矩阵中各元素代表不同感知预测时刻零件的残余应力变形量,即在不同感知时刻释放装夹时零件不同感知预测位置的残余应力变形量。其中,Di=[Di1 Di2 … Dik],代表第i个感知时刻,零件不同位置的残余应力变形值。需要注意的是,各元素取值位置不一定与装夹力感知位置对应。
实现感知系统最关键的是获得感知量矩阵与目标矩阵之间的映射关系f,根据该映射关系可通过感知量矩阵求解目标矩阵,从而实现对残余应力变形的感知预测。该映射关系可通过理论推导、有限元仿真或者智能算法等获得。
在真实的加工过程中,材料的切除过程主动引入了残余应力或者造成了内部残余应力的失衡。这相当于给整个感知系统施加了一个激励,造成了感知量矩阵的变化。若对感知过程进行简化,只感知加工完成之后的装夹力变化,加工的激励造成感知量矩阵ΔF的出现,根据已经建立的感知映射关系,即感知量矩阵到目标矩阵的关系f:ΔF→D,即可完成对目标矩阵D的有效预测,相应地也就建立了感知系统的数学模型。
从以上叙述可以看到,感知系统的数学模型需要从三方面进行构建。一是感知量矩阵的定义,主要是确定感知手段、感知时刻及感知位置。残余应力变形感知手段监测装夹力的变化,主要是在特定装夹位置安装力传感器,监测加工前后装夹力的变化值;感知时刻可随着加工工艺的需求确定;而感知位置可根据仿真或者试件加工的结果,确定弱刚度位置,施加装夹感知点来确定。二是目标矩阵的定义,主要是确定残余应力变形的预测评估位置。这一点主要根据工艺要求来确定,在零件精度要求高的位置定义评估点;若精度要求一致,则在易变形的位置定义评估点,控制最大残余应力变形。三是映射关系,由于零件结构的复杂性,往往很难通过理论求解的方式获得映射关系,因此需要通过仿真或者智能算法的方式获得该映射关系。
6.5 典型装夹形式残余应力变形势能感知
图6.5所示为装夹过程中常用的两种工件-夹具接触方式,图6.5(a)所示为法向力接触,图6.5(b)所示为法向力-双向摩擦力接触。在工件中引入了残余应力变形势能之后,单纯的法向力接触较少,在残余应力等效力矩的作用下,装夹接触多为法向力-双向摩擦力接触方式。采用三向力传感器感知装夹力的变化,能够获得较为精确的结果。但在实际应用中,特别是在薄壁零件加工中,多余约束的存在大多限制工件沿壁厚方向的变形与振动,工件在壁厚方向的刚度远远小于其他方向的刚度,残余应力引入导致的变形也多为壁厚方向的变形。此时法向接触力的变化值要远远大于摩擦力的变化值,采用单向力传感器感知法向接触力的变化也能够较为准确地求解感知预测模型。

图6.5 典型的工件-夹具接触形式
(a)法向力接触(b)法向力-双向摩擦力接触
下面的分析忽略了装夹接触切向力的变化,重点分析法向弹性接触力的变化。可以采用单向压力传感器监测装夹力的变化,进而预测工件的残余应力变形。
6.5.1 多余约束中存在面约束
如图6.6所示,实际应用中,常用的多余约束中存在面约束的装夹形式有三种,分别为面支撑装夹、点对面装夹和面对面装夹。根据式(6.9),残余应力变形感知模型的求解需要感知获得特定位置的装夹力变化。对于多余约束中存在面约束的装夹方式,残余应力变形势能引入所导致的等效力矩被多余约束对工件的装夹力变化值产生的力矩抵消。其数学表达式为
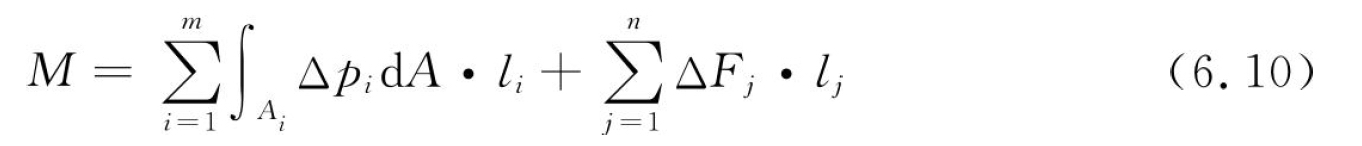
式中:M为残余应力等效力矩;m为面约束数量;Ai为面约束装夹接触面积;n为点约束数量;Δp为面约束接触面上的接触应力增量;ΔF为点约束上的接触力增量;l为装夹力力臂。
面约束接触合力数值可以通过在夹具上安装压力传感器感知得到。但是,当加工完成,工件引入残余应力变形势能之后,工件一端引入了等效力矩。由于面约束装夹接触是一个面,此时夹具对工件的装夹力并不是正对施加的,现有的技术很难直接通过传感的方法获得准确的合力位置。面接触装夹力作用位置的不确定使得感知模型无法准确求解。但在实际应用中,当夹具装夹面相对于整个工件尺寸而言足够小时,可近似认为装夹力施加位置在装夹面的正中。
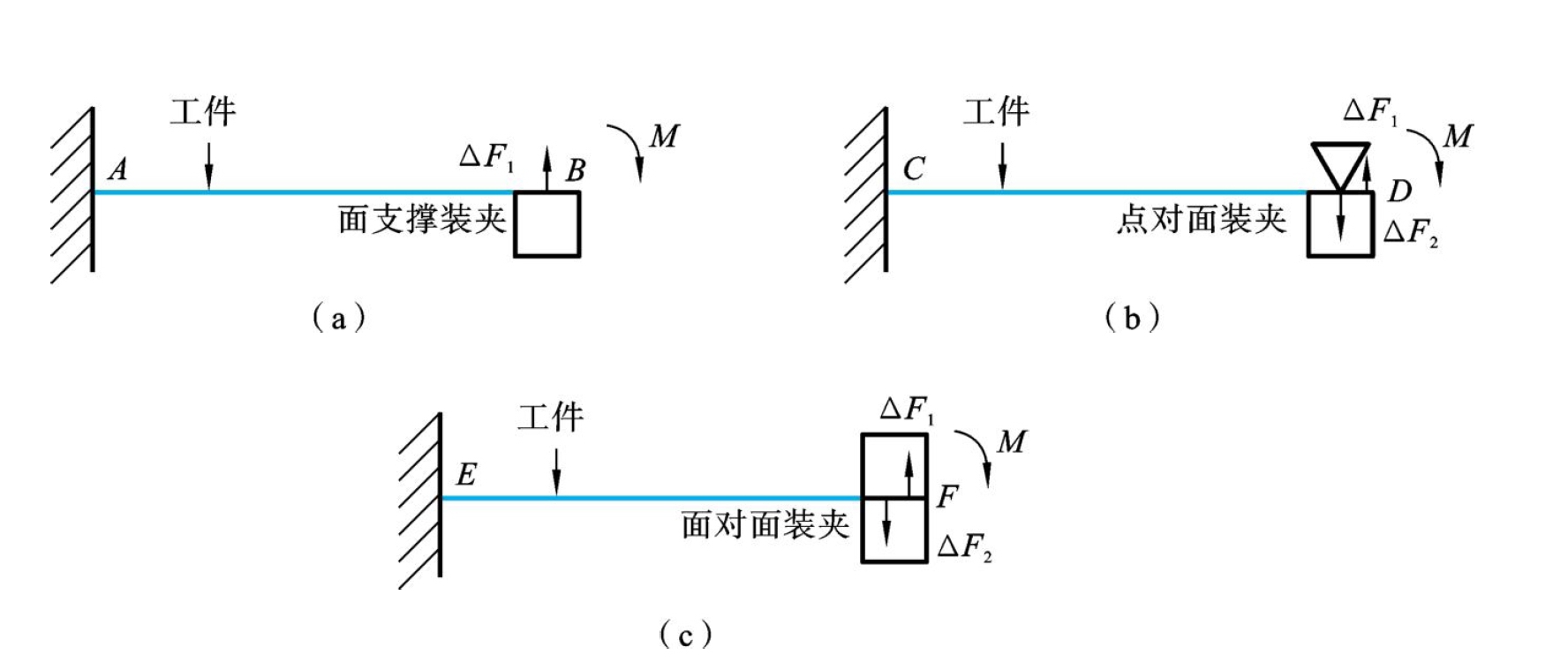
图6.6 典型面约束装夹系统
(a)面支撑装夹形式(b)点对面装夹形式(c)面对面装夹形式
6.5.2 多余约束为点约束
如图6.7所示,实际应用中多余约束为点约束存在两种装夹形式,一种是点支撑形式,另外一种为点对点装夹形式。
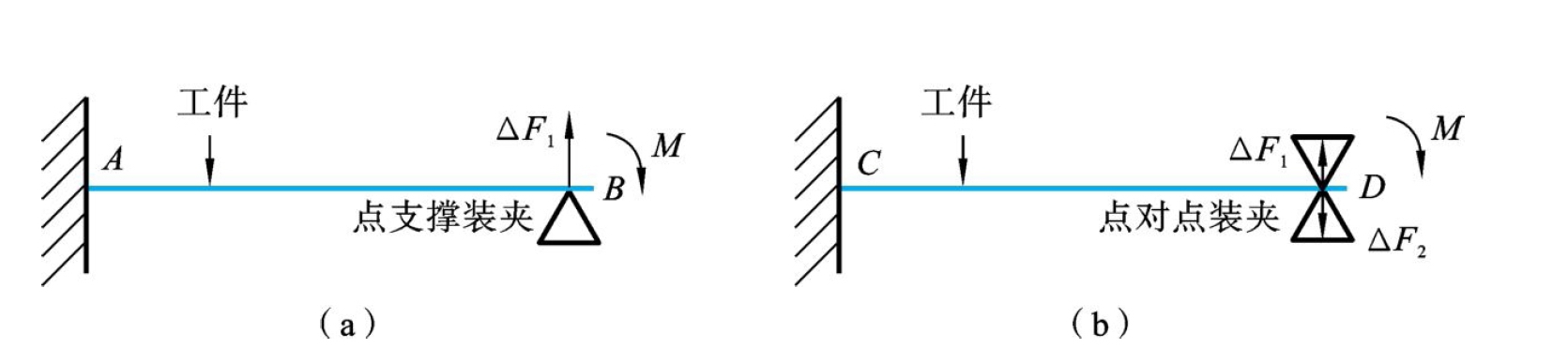
图6.7 典型点约束装夹系统
(a)点支撑装夹形式(b)点对点装夹形式
对于点约束装夹形式,其残余应力等效力矩平衡关系为

通过在点约束上安装压力传感器就可以准确感知获得特定约束位置的装夹力,即式(6.11)右侧元素均可准确感知获得。在此种装夹形式下可准确求解残余应力变形感知预测模型。但是应用支撑进行变形感知时,需要预估变形方向,使得支撑位置上工件变形压迫支撑。
如图6.8所示,在实际感知过程中,由于装夹形式的限制,以及零件结构形式和表面形状的复杂性,在装夹过程中往往难以保证传感器感知方向完全与该装夹点处的工件表面法向保持一致。此时,感知到的装夹力为实际接触力向感知杆轴向的分解数值,可通过感知力反求接触力数值用于残余应力变形感知预测模型的求解,求解公式如下:

式中:F为感知位置装夹力变化值;Fs为传感器感知到的压力变化值;α和β分别为曲面的法向量和传感器的轴向量。
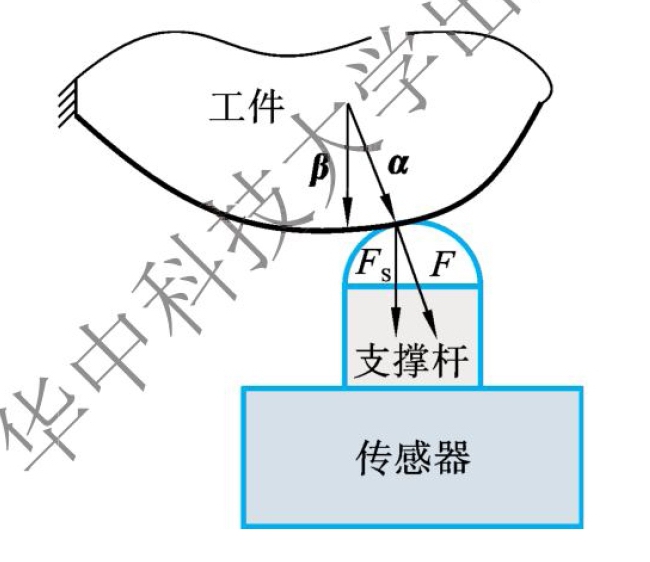
图6.8 曲面点约束示意图
6.6 残余应力变形感知预测模型求解
为保证装夹的稳定性,数控加工中工件多采用超静定装夹方式。装夹系统中除了维持几何不变的必需约束外还存在一些多余约束。定义装夹系统维持几何不变的必需约束与工件组成的结构为装夹系统的静定基。静定基可以有不同的选择,并不是唯一的。薄壁零件装夹系统的多余约束多为辅助支撑,用以提高系统的刚性,减小加工过程中机械载荷造成的振动以及变形。
在超静定装夹系统中,根据弹性力学相关理论,应用变形叠加原理和变形协调方程可以实现对残余应力变形感知预测模型的求解,求解公式为
式中:DM为零件上各变形势能感知点装夹释放后的残余应力变形;δ为零件上各感知点在任一单位装夹力作用下的变形。此式表明,工件装夹卸载后的残余应力变形等于装夹力变化值的反力单独作用在工件上引起的变形。
以平板装夹系统为例来进行一次超静定装夹系统的残余应力变形感知预测模型的求解。图6.9(a)所示为一个三维的窄板单面铣削装夹系统,工件为平板,一端采用压板或者螺栓固支,一端采用辅助支撑简支。辅助支撑上安装有压力传感器用以监测支撑力的变化。装夹结构中存在一个多余约束,它是一次超静定装夹系统。
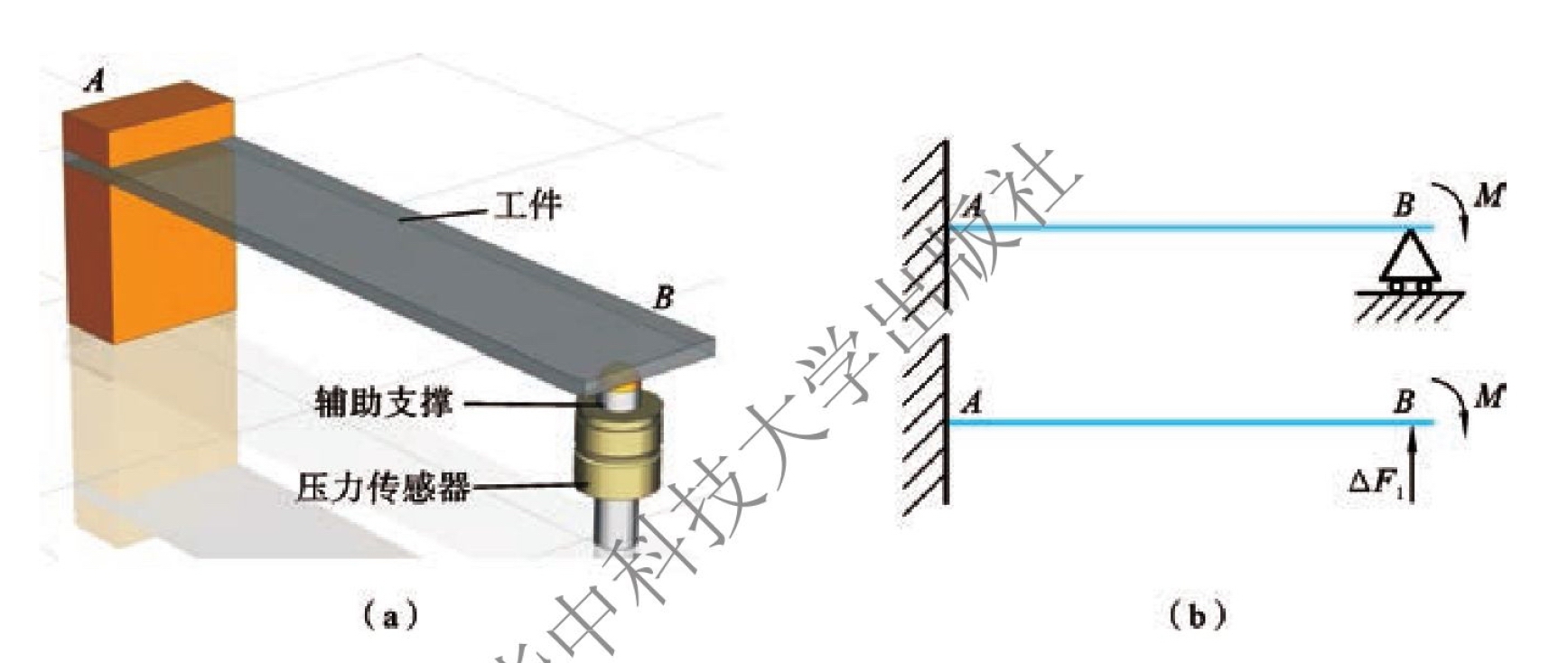
图6.9 一次超静定装夹系统分析
(a)一次超静定装夹系统(b)二维简化受力状态
铣削加工过程中刀具切削材料在工件上表层引入残余压应力,使工件发生上凸变形。将工件简化为梁,则装夹系统可简化为简支梁结构,其载荷作用情况如图6.9(b)所示。加工过程在工件中引入残余压应力,残余压应力对平板变形产生的作用可以用施加在平板一端的力矩M进行等效。若不存在多余约束B,则工件即时发生弯曲变形。由于多余约束B对工件作用多余约束力ΔF,工件在装夹状态下未发生变形。残余应力引入的能量以变形势能的形式存储在工件中。解除多余约束B,以多余约束力ΔF1代替。多余约束力ΔF1即为压力传感器感知到的支撑力变化值。在ΔF1与M的共同作用下,工件B端支撑点沿F1方向产生位移,定义为D1。可以认为D1由两部分组成:一部分是静定基在残余应力等效力矩M单独作用下产生的D1M,另一部分是静定基在多余约束力ΔF1作用下产生的位移D1F,即
式中:位移记号的第一个下标1代表位移发生在B端F1作用点且沿F1的方向。
由于辅助支撑B的存在,B端不发生位移,因此有
在计算D1F时,可以在静定基上沿F方向施加单位力,B点沿F1方向因单位力作用产生的位移记为δ11。对于线弹性结构,位移与力的大小成正比,故D1F为δ11的ΔF1倍,代入公式(6.15),可得
式(6.16)左边为多余约束释放后工件的残余应力引起的变形,右边为支撑力变化反力在静定基上引起的变形。式中ΔF1可通过装夹力监测的方式获得,δ11可通过理论推导或者仿真的方式获得。这样就建立起了感知量目标矩阵与感知量矩阵之间的映射关系,实现了一次超静定装夹系统残余应力变形感知预测模型的求解。
将上述方法推广到二次超静定装夹系统。图6.10所示的超静定装夹结构存在两个多余约束B和C,铣削完成后对其进行受力分析,加工过程引入的残余应力作用以等效力矩代替,多余约束产生两个约束反力。同样解除多余约束B和C,以多余约束力ΔF1和ΔF2代替,那么在多余约束B和C位置的变形协调方程便可以表示为
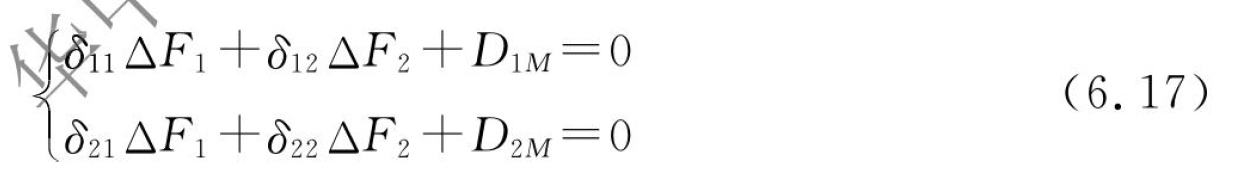
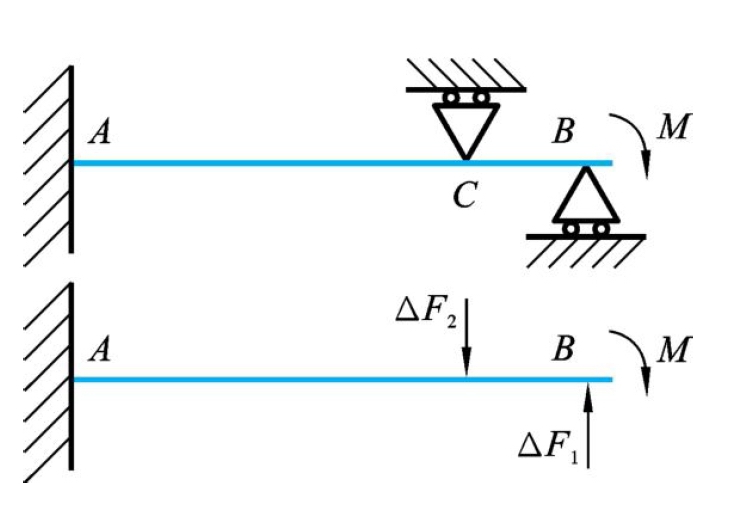
图6.10 二次超静定装夹系统分析
装夹去除后的残余应力变形即为
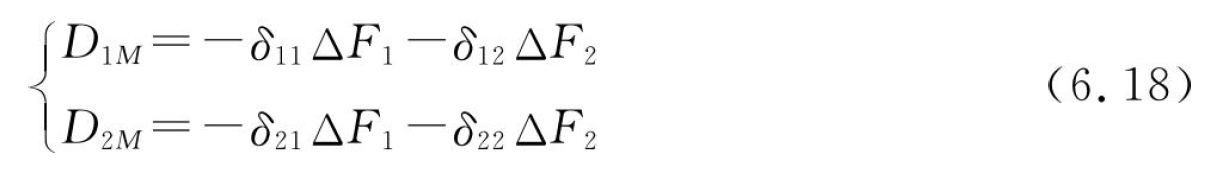
从上述求解过程可以看到,残余应力场作用下的变形协调方程的推导未涉及零件结构,因此进一步地将上述方法推广到n次超静定装夹系统残余应力变形感知的求解,如图6.11所示,则在不同的感知点有以下变形协调方程组:
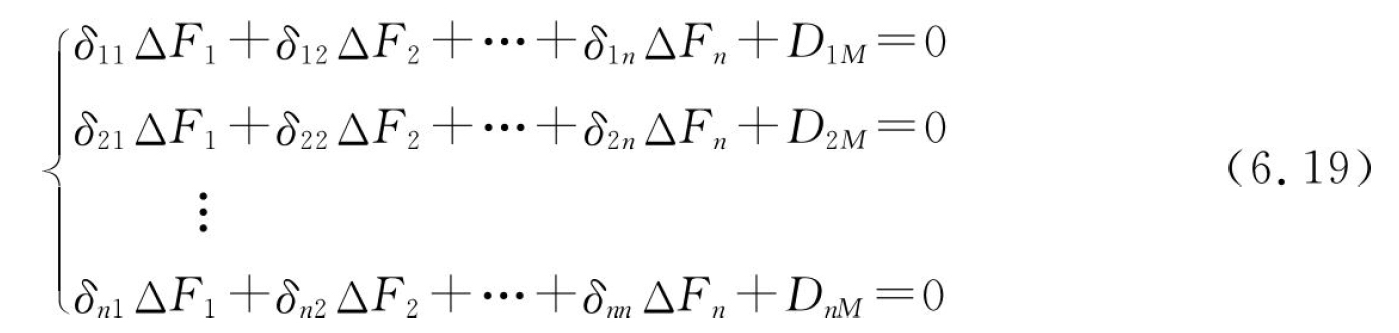
式中:ΔFi代表各多余约束上约束力的变化值;δij代表静定结构在ΔFj=1单独作用时沿Fi方向的位移;DiM代表静定基结构在残余应力单独作用下,沿Fi方向的位移。
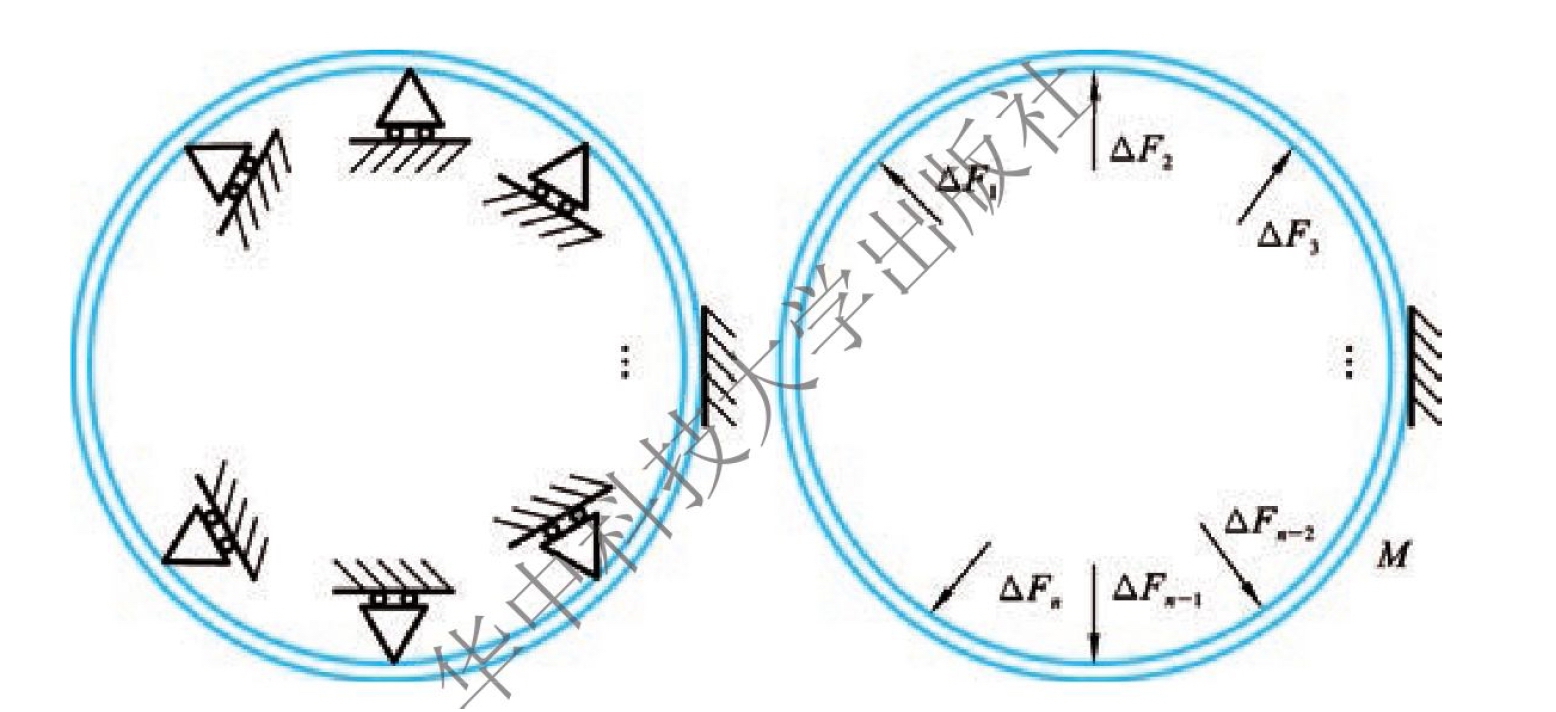
图6.11 n次超静定装夹系统
由位移互等定理,力ΔFi在Fj作用点沿Fj方向引起的位移等于力ΔFj在Fi作用点沿Fi方向引起的位移,即上述方程组中的系数存在以下关系:
应用该公式可简化方程组系数的求解,系数求解可采用理论推导或者仿真的方式进行。
从上述求解过程中可以看出,基于装夹力监测的残余应力变形感知预测方法能够准确获得感知点的残余应力变形数值,但是对非感知点的评估需要通过位移场拟合的方式获取。这就意味着,对感知距离较远的点的残余应力变形的预测效果存在一定的不确定性,因此需要合理规划感知点的分布,对精度要求高、变形刚度小的区域全面感知,确保变形不超差。
结合上述提出的感知模型、模型求解方法以及感知过程的讨论,残余应力变形的感知预测实现步骤如下。
(1)感知点选取。通过仿真或者理论分析的方法,预估工件可能的变形状态。此时可简化工件结构、残余应力分布等,大致预估变形趋势即可,在变形较大的部位施加感知点。
(2)装夹方案设计。多余约束为点接触时,感知点的残余应力变形可进行准确求解,因此在进行装夹设计时,在保证装夹稳定的同时,尽量采用点装夹形式作为多余约束,将夹紧力传感器安装于其上;若必须采用面装夹形式,则应尽量缩小装夹面面积,近似求解变形值。
(3)加工感知。装夹工件,按照给定工况完成工件的加工。在感知时间点记录装夹力的数值。
(4)变形求解。建立工件装夹系统静定基的有限元模型,在感知位置施加装夹力变化值的反力,得到工件的变形状态。此时的变形状态即为工件装夹卸载后的残余应力变形值。
6.7 薄壁零件加工残余应力变形感知应用案例
材料为GH4169材料薄板,尺寸为160 mm×20 mm×2 mm,取中间区域加工80 mm×20 mm的表面,加工深度为0.5 mm,两端各留40 mm×20 mm的区域用于装夹。薄板件在加工前经过去应力热处理,残余应力变形主要由表层加工残余应力导致。下面介绍该薄壁零件加工残余应力变形感知的实现方法。
6.7.1 感知位置的确定
为确定感知位置,在有限元分析软件中建立薄板件装夹系统静定基的加工残余应力变形预测分析有限元模型,通过仿真零件在一定应力分布下的加工残余应力变形,确定弱刚度位置,确定感知点,过程如下所述:
(1)模型的建立及设置。建立薄板的三维模型,采用薄壳绑定的方式将薄板加工面表层划分为7层,每层15μm,此为加工残余应力的作用区域。设置薄板材料为GH4169,薄板一端固定约束,采用八节点六面体实体单元划分网格,工件离散为192000个单元。
(2)残余应力的施加。将表6.1所示残余应力分布按深度施加到各层上。此残余应力为采用试验所用参数铣削加工GH4169材料块后通过X射线衍射测量得到的。若采用变工况加工,由于固定刀具在一定工况范围内切削残余应力具有相似的分布特性,可将在加工表层施加该工况范围内的某一参数下的残余应力分布用于最大变形位置的评估。
表6.1 加工表层残余应力分布

(3)残余应力变形的计算及后置处理。根据有限元计算结果,获得工件铣削加工后的变形云图,通过有限元模型获得静定装夹下工件的残余应力变形状态,如图6.12所示。从图中可以看到,薄壁零件单面加工整体呈现弯曲变形,最大变形位置位于工件长度方向边界处。考虑实际装夹限制,一端装夹与零件成为静定基,则将感知点设置在距边界10 mm宽度中点处。
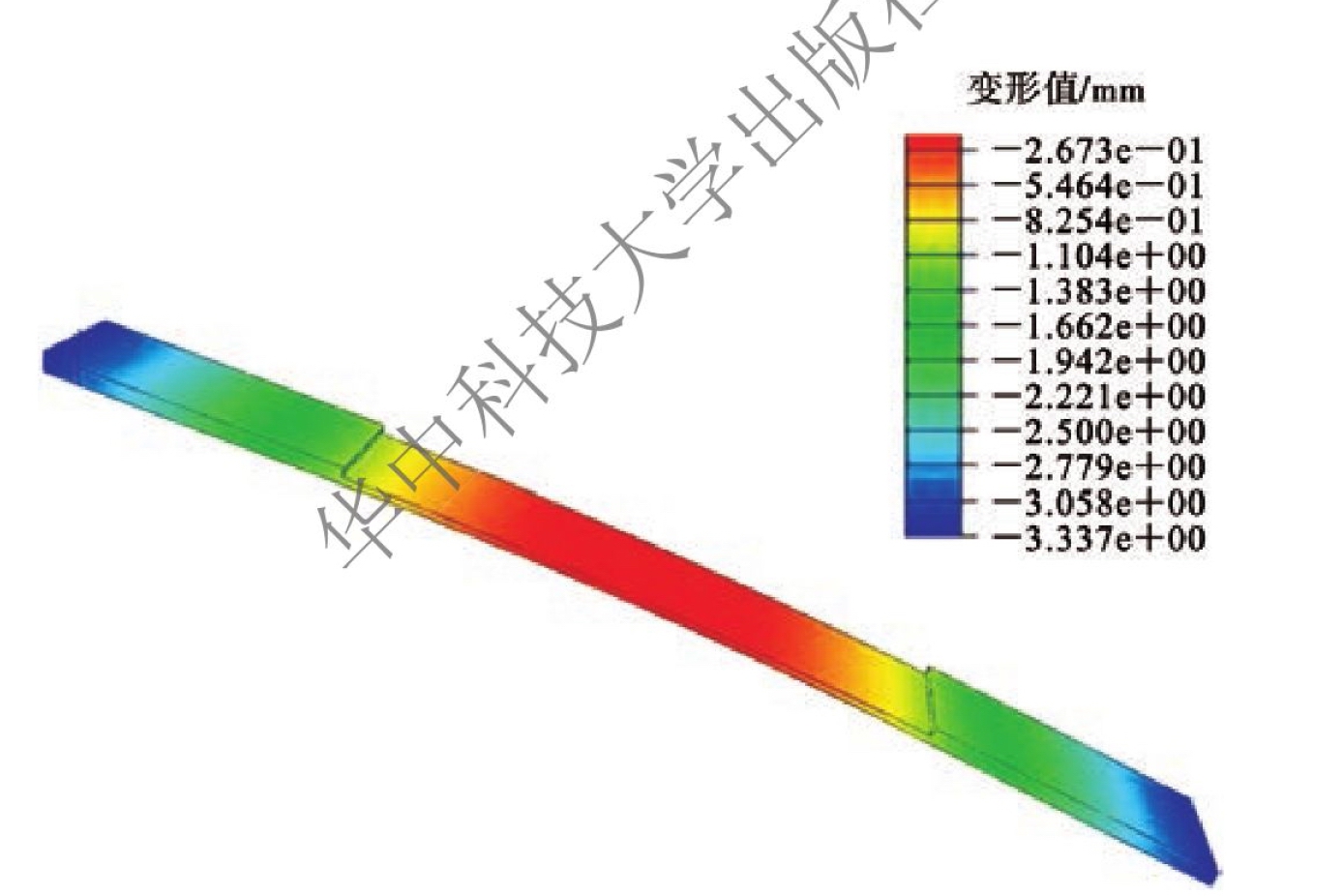
图6.12 残余应力变形云图
6.7.2 感知夹具的设计
夹具设计如图6.13所示,采用一端夹紧,一端点对点装夹的方式。点对点端上下各安装一个压力传感器,传感器与工件接触面为圆弧面点接触。为了确保点对点位置的准确定位,上下夹具部件上对应位置各有三个螺纹定位孔,与传感器上螺纹孔一起确保传感器安装位置的准确性,上下夹具部件采用嵌套的方式装配,确保点对点装夹。另外,为防止出现加工中振松装夹点的现象,螺栓采用自锁螺母固定,确保加工前后装夹力变化由残余应力引入所导致。
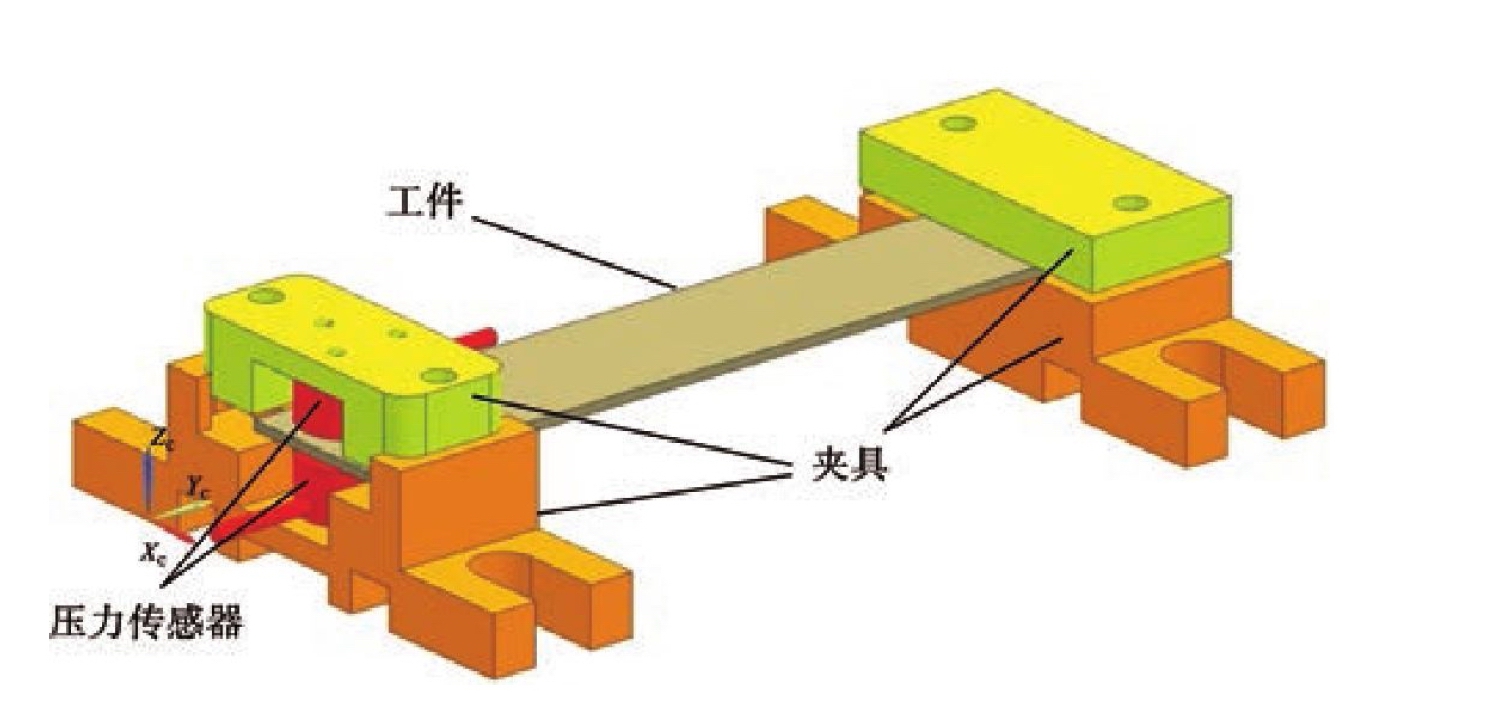
图6.13 平板装夹系统
6.7.3 加工感知实验
实验采用两齿平底铣刀加工,切深为0.5 mm,切宽为2 mm,切削速度为80 m/min。采用高精度数采仪获取夹紧力数值。加工前通过数采仪获得夹具上部传感器感知值为31.6 N,下部传感器感知值为32.8 N。经传感器校核,上下夹紧力的偏差是由传感器线性度偏差导致的。偏差值较小,且实验需要获取的是数值较小的装夹力的变化值,该偏差对实验结果影响很小。加工后,上传感器感知值为31.3 N,下传感器感知值为33.2 N。加工完成后卸载感知端装夹,利用变形测量设备测量工件沿长度中线方向的变形。
6.7.4 变形的求解
由感知结果可知,薄壁零件上部点装夹对平板的作用力变化为-0.3 N,方向向下;下部点装夹对平板的作用力变化为0.4 N,方向向上。按照求解公式,薄壁零件残余应力变形等效为在工件上下表面感知位置各施加向下的0.3 N和0.4 N的载荷产生的变形值。在有限元分析软件中建立有限元仿真模型,在感知点施加向下的载荷获得工件的变形云图,提取沿长度中线的变形数值。感知预测结果与实测结果对比如图6.14所示,实测最大变形为1.07 mm,感知预测最大变形为0.93 mm,最大感知预测误差为13%。
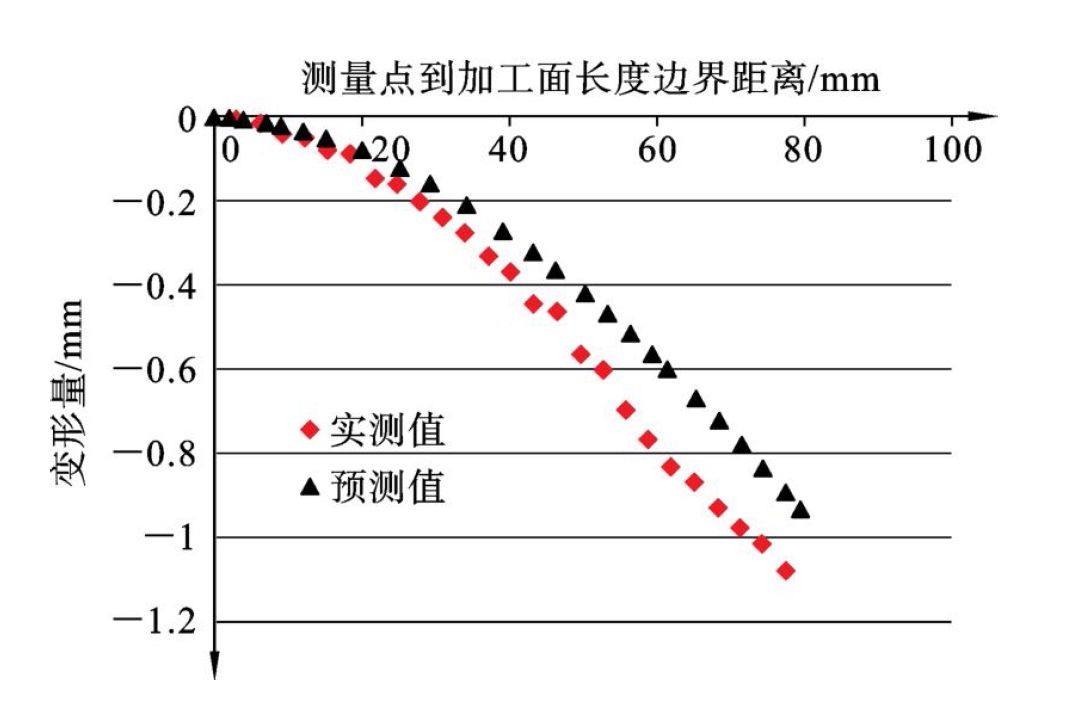
图6.14 感知预测结果与实测结果对比
本章参考文献
[1]王骏腾.薄壁件铣削残余应力变形的感知预测与工艺优化方法[D].西安:西北工业大学,2019.
[2]WANG J T,ZHANG DH,WU B H,et al.Prediction of distortion induced by machining residual stresses in thin-walled components[J].The International Journal of Advanced Manufacturing Technology,2018,95(9):4153-4162.
[3]杨吟飞.基于内应力场的整体结构件加工变形预测和控制技术研究[D].南京:南京航空航天大学,2010.
[4]张培信.能量理论结构力学[M].上海:上海科学技术出版社,2010.
