三、证券市场线
资本市场线反映的是有效组合的预期收益率和标准差之间的关系,任何单个风险证券由于不是有效组合因而一定位于该直线的下方。因此,资本市场线并不能告诉我们单个证券的预期收益与标准差之间存在怎样的关系。为此,我们有必要做进一步分析。投资组合的标准差可用公式10-2表示。
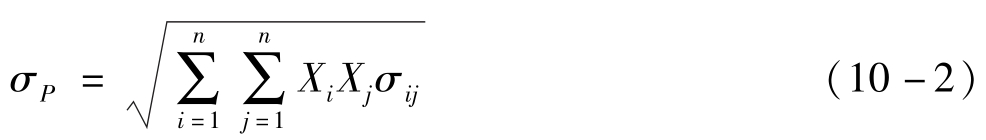
根据公式10-2可以得出市场组合标准差的计算公式为10-3。
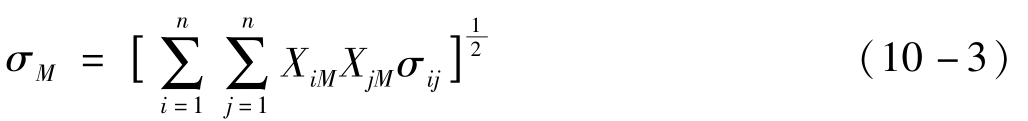
其中,XiM和XjM分别表示证券i和j在市场组合中的比重。10-3可以展开为公式10-4。
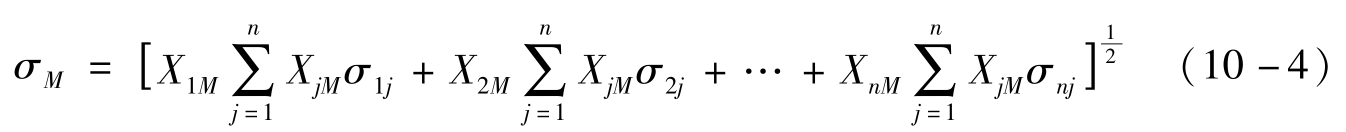
根据协方差的性质,证券i与市场组合的协方差σiM等于证券i与市场组合中每种证券的协方差的加权平均数,如公式10-5所示。

如果将协方差的这个性质运用于市场组合中的每一个风险证券,并代入式子中,可以得到公式10-6。
其中,σ1M表示证券1与市场组合的协方差,σ2M表示证券2与市场组合的协方差,依此类推。上式表明,市场组合的标准差等于所有证券与市场组合协方差的加权平均数的平方根,其权重为各种证券在市场组合中的比例。
由此可见,在考虑风险时,重要的不是各种证券自身的整体风险,而是其与市场组合的协方差。这就是说,自身风险较高的证券,并不意味着其预期收益率也应较高;同样,自身风险较低的证券,也并不意味着其预期收益率也就较低。单个证券的预期收益率水平应取决于其与市场组合的协方差。
因此,可以得出如下结论:具有较大σiM值的证券必须按比例提供较高的预期收益率以吸引投资者。由于市场组合的预期收益率和标准差分别是各种证券的预期收益率和各种证券与市场组合的协方差(σiM)的加权平均数,其权重均等于各种证券在市场组合中的比例。因此,如果某种证券的预期收益率相对于其σiM值太低的话,投资者只要把这种证券从其投资组合中剔除就可提高其投资组合的预期收益率,从而导致证券市场失衡。同样,如果某种证券的预期收益率相对于其σiM值太高的话,投资者只要增持这种证券就可提高其投资组合的预期收益率,从而也会导致证券市场失衡。在均衡状态下,单个证券的风险和收益的关系可以表示为公式10-7。
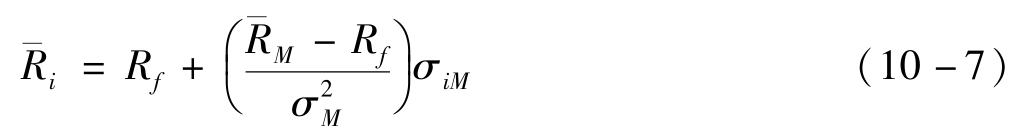
上式所表示的就是著名的证券市场线(security market line,SML),它反映了单个证券与市场组合的协方差和其预期收益率之间的均衡关系,如果用纵轴表示![]() 用横轴表示σiM,则证券市场线在图上就是一条截距为Rf、斜率为
用横轴表示σiM,则证券市场线在图上就是一条截距为Rf、斜率为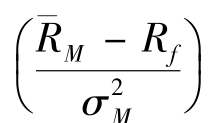 的直线,如图10-3(a)所示。
的直线,如图10-3(a)所示。
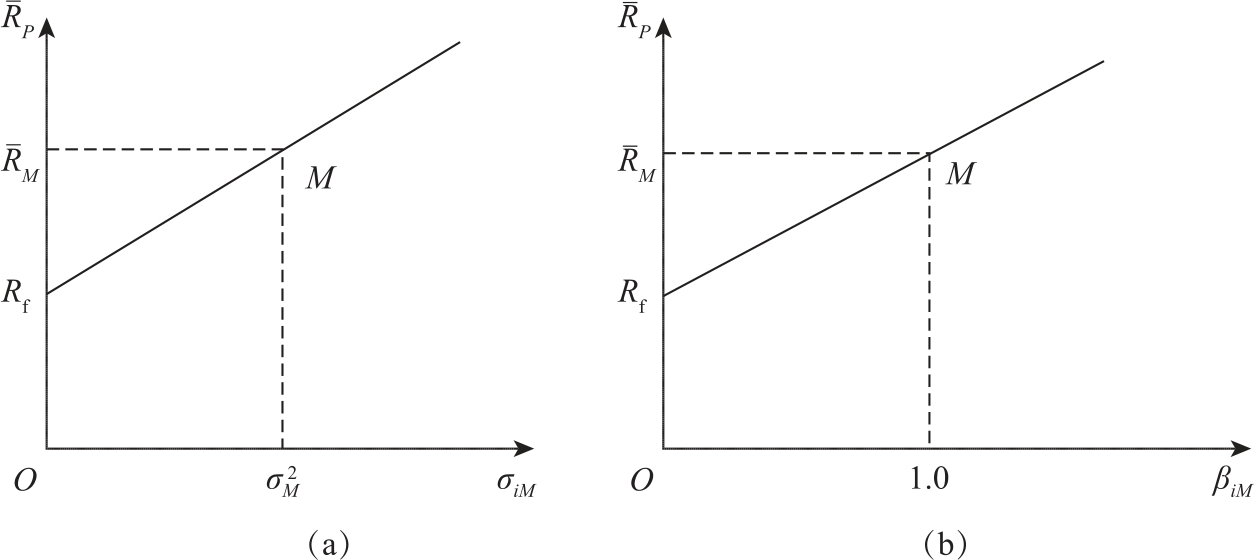
图10-3 证券市场线
从上式可以发现,对于σiM等于0的风险证券而言,其预期收益率等于无风险利率,因为这个风险证券与无风险证券一样,对市场组合的风险没有任何影响。更有趣的是,当某种证券的σiM<0时,该证券的预期收益率甚至低于Rf。
令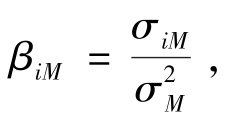 可以得到公式10-8。
可以得到公式10-8。
其中,βiM称为证券i的β系数,它是表示证券i与市场组合协方差的另一种方式。上式是证券市场线的另一种表达形式。如果用纵轴表示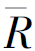 i,用横轴表示βiM,则证券市场线也可表示为截距为Rf,斜率为(
i,用横轴表示βiM,则证券市场线也可表示为截距为Rf,斜率为(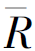 M-Rf)的直线,如图10-3(b)所示。
M-Rf)的直线,如图10-3(b)所示。
β系数的一个重要特征是,一个证券组合的β值等于该组合中各种证券β值的加权平均数,权重为各种证券在该组合中所占的比例,即如公式10-9所示。

其中,βPM表示组合P的β值。
由于任何组合的预期收益率和β值都等于该组合中各个证券预期收益率和β值的加权平均数,其权重也都等于各个证券在该组合中所占比例,因此,既然每一种证券都落在证券市场线上,那么由这些证券构成的组合也一定落在证券市场线上。
通过比较资本市场线和证券市场线可以看出,只有最优投资组合才落在资本市场线上,其他组合和证券则落在资本市场线的下方。而对于证券市场线而言,无论是有效组合还是非有效组合,它们都落在证券市场线上。
既然证券市场线包括了所有证券和所有组合,那么它也一定包含了市场组合和无风险资产。在市场组合那一点,β值为1,预期收益率为![]() 因此其坐标为
因此其坐标为![]() 在无风险资产那一点,β值为0,预期收益率为Rf,因此其坐标为(0,Rf)。证券市场线反映了在不同的β值水平下,各种证券及证券组合应该实现的预期收益率水平,从而反映了各种证券和证券组合系统性风险与预期收益率的均衡关系。由于预期收益率与证券价格成反比,因此证券市场线实际上也给出了风险资产的定价公式。
在无风险资产那一点,β值为0,预期收益率为Rf,因此其坐标为(0,Rf)。证券市场线反映了在不同的β值水平下,各种证券及证券组合应该实现的预期收益率水平,从而反映了各种证券和证券组合系统性风险与预期收益率的均衡关系。由于预期收益率与证券价格成反比,因此证券市场线实际上也给出了风险资产的定价公式。
资本资产定价模型所揭示的投资收益与风险的函数关系,是通过投资者对持有证券数量的调整并引起证券价格的变化而达到的。根据每一证券的收益和风险特征,给定一个证券组合,如果投资者愿意持有的某一证券的数量不等于已持有的数量,投资者就会通过买进或卖出证券进行调整,由此对这种证券价格产生上涨或下跌的压力。在实现一组新的价格水平后,投资者将重新估计对各种证券的需求,这一过程将持续到投资者对每一种证券愿意持有的数量等于已持有的数量为止,此时证券市场达到均衡。
