7.4.2　稳健性检验

Order Probit模型的ML和简单线性回归模型的OLS在参数估计的方向和显著性上存在一致性。因此，本文试图尝试使用Order Probit模型验证模型的稳定性。根据研究需要，本文将应答者在5项融入指标上的得分加总，然后再重新赋值，划分出5类来度量被公众所感知和认可的移民融入度，如表7-13所示。

表7-13　移民融入度指标等级重构

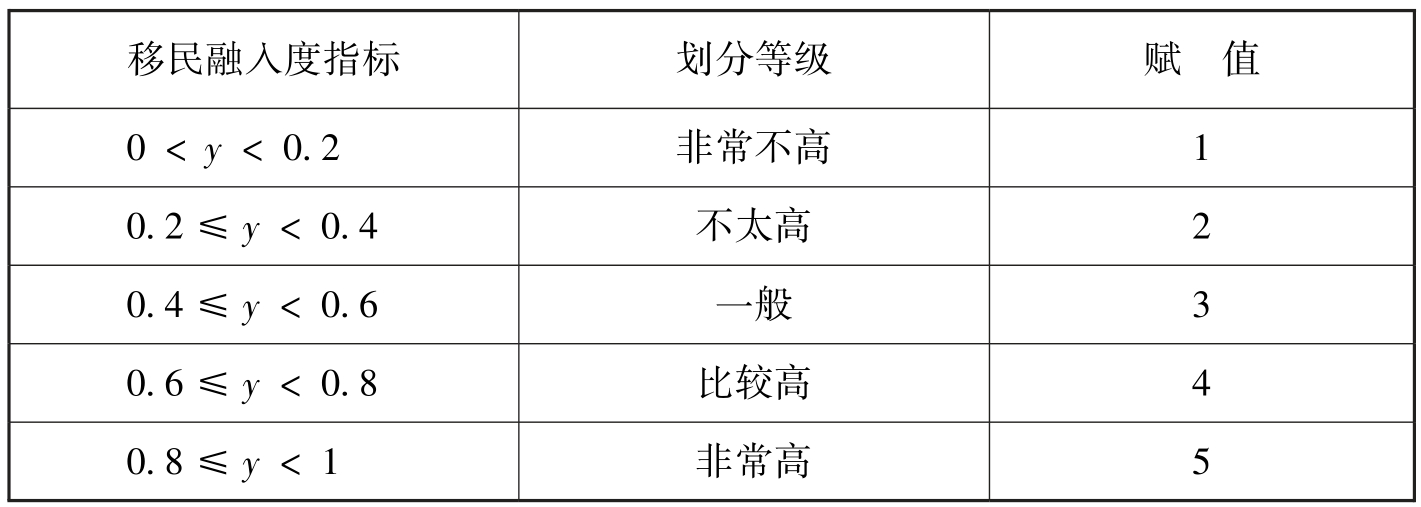
通过对移民融入度与移民个体和宏观因素间的关系的探讨，得出了一些基本的理论。但利用主观评价度量移民融入度，会存在一个问题，即被访者可能存在谎报选择，比如出于免费搭便车动机而策略性地低报，也可能出于对访谈者的礼貌而高报。在不能观测到具体哪些受访者会“高报”或“低报”时，借鉴高琳的做法对移民融入度的评价等级重新赋值。赋值规则是，受访者“低报”时，将非常高、比较高和一般的得分者合并为“高移民融入度者”且赋值为1，将非常不高、不太高的得分者合并为“低移民融入度者”且赋值为0。受访者“高报”时，将非常高、比较高的得分者合并为“高移民融入度者”且赋值为1，将一般、不太高、非常不高的得分者合并为“低移民融入度者”且赋值为0。进行重新赋值后应用二值Order Probit模型进行估计。回归结果见表7-14，无论受访者存在“低报”或“高报”，个体因素和宏观变量对移民融入度的影响系数仅是发生了大小上的微弱改变，符号方向和显著程度都没发生改变。这说明了受访者谎报满意度水平不是值得担忧的问题，本文的估计结果是稳健可靠的。

除了改变验证模型的方法，本文还从数据出发，根据不同的标准调整分类，检验结果是否依然显著。在移民年龄划分标准中，基本回归时考察了相比五六十年代移民，其余年代的移民融入呈显著性。为深入考察移民代际问题对于融入度的影响，将1980年前出生者赋值为0，将1980年后出生者细分，分为1980—1990年出生和1990年后出生两个阶段，分别赋值为1，纳入回归方程。稳健性检验结果如表7-15所示，关键解释变量的回归系数和p值变动细微，说明模型稳健性良好，在针对1980—1990年出生者的回归中，系数显著为正，拟合优度出现上升，其他控制变量的显著度并未发生改变。这说明1980—1990年出生者融入度略高于1980年前出生的人。对1990年后出生者的回归中拟合优度出现下降，但浮动比率变化不大，这与符合划分标准的样本数量骤减存在一定关系，且控制变量中的显著度基本无变化，说明模型较为稳健。

表7-14　基于Order Probit回归模型的稳健性检验

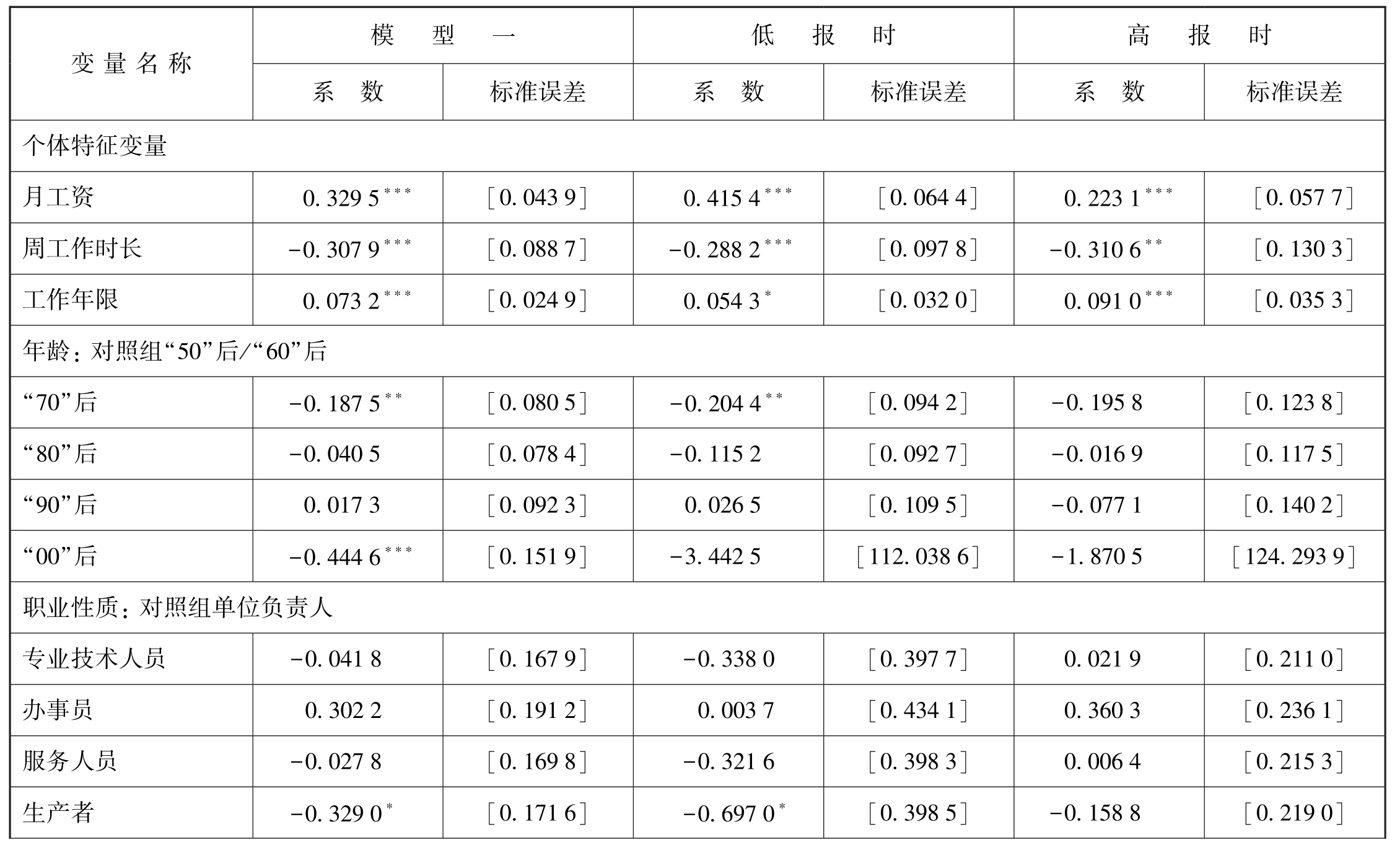
续　表

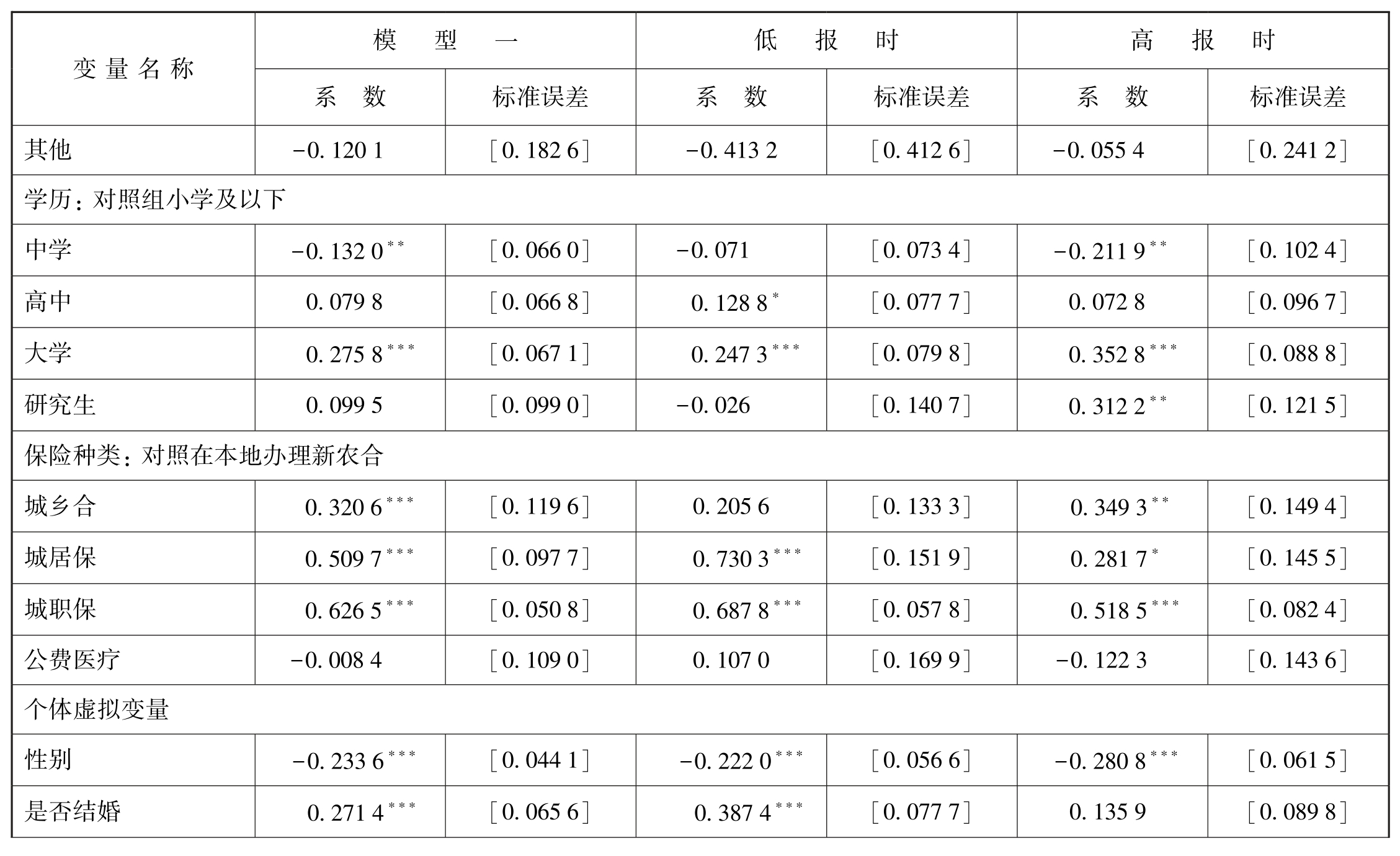
续　表

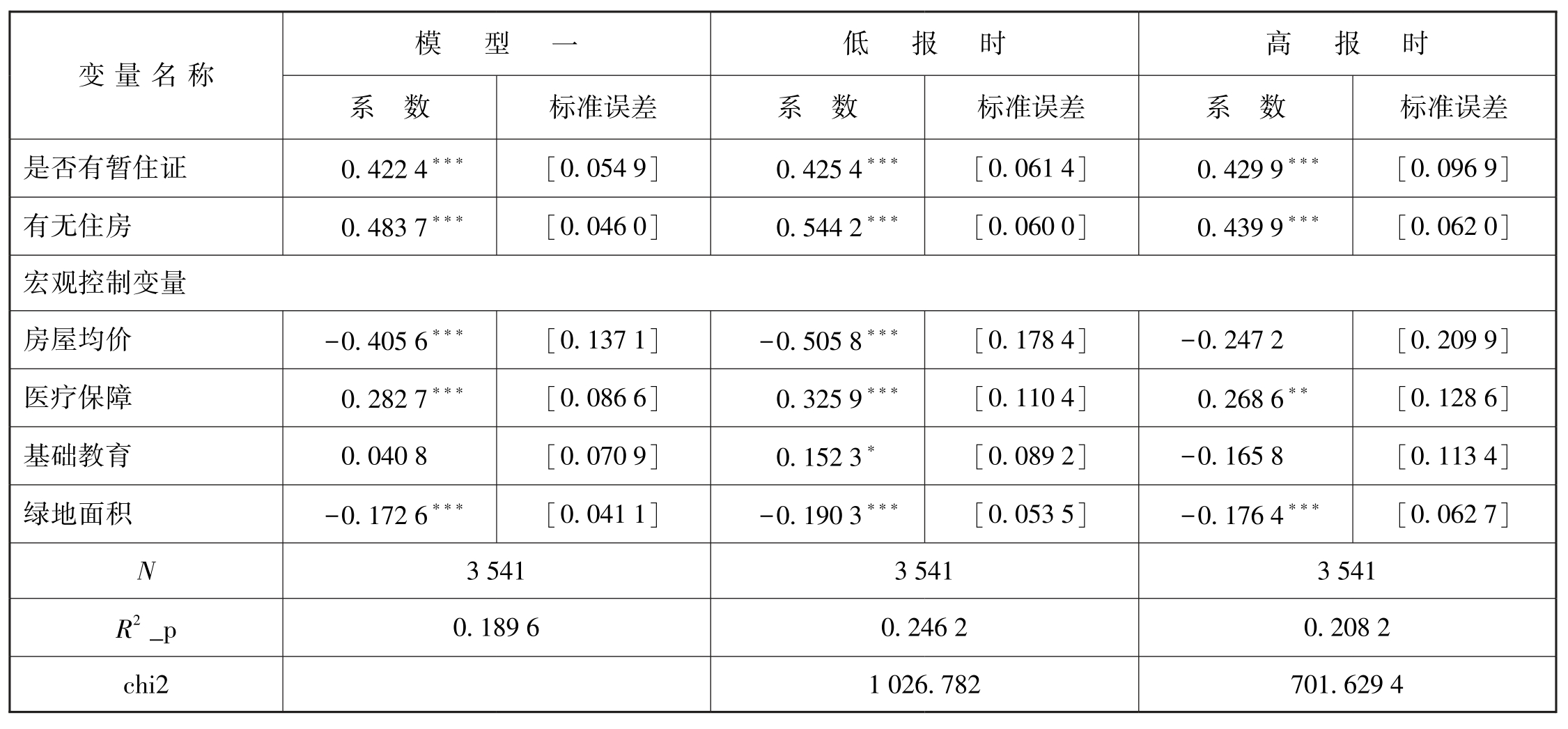
表7-15　基于改变代际划分的稳健性检验

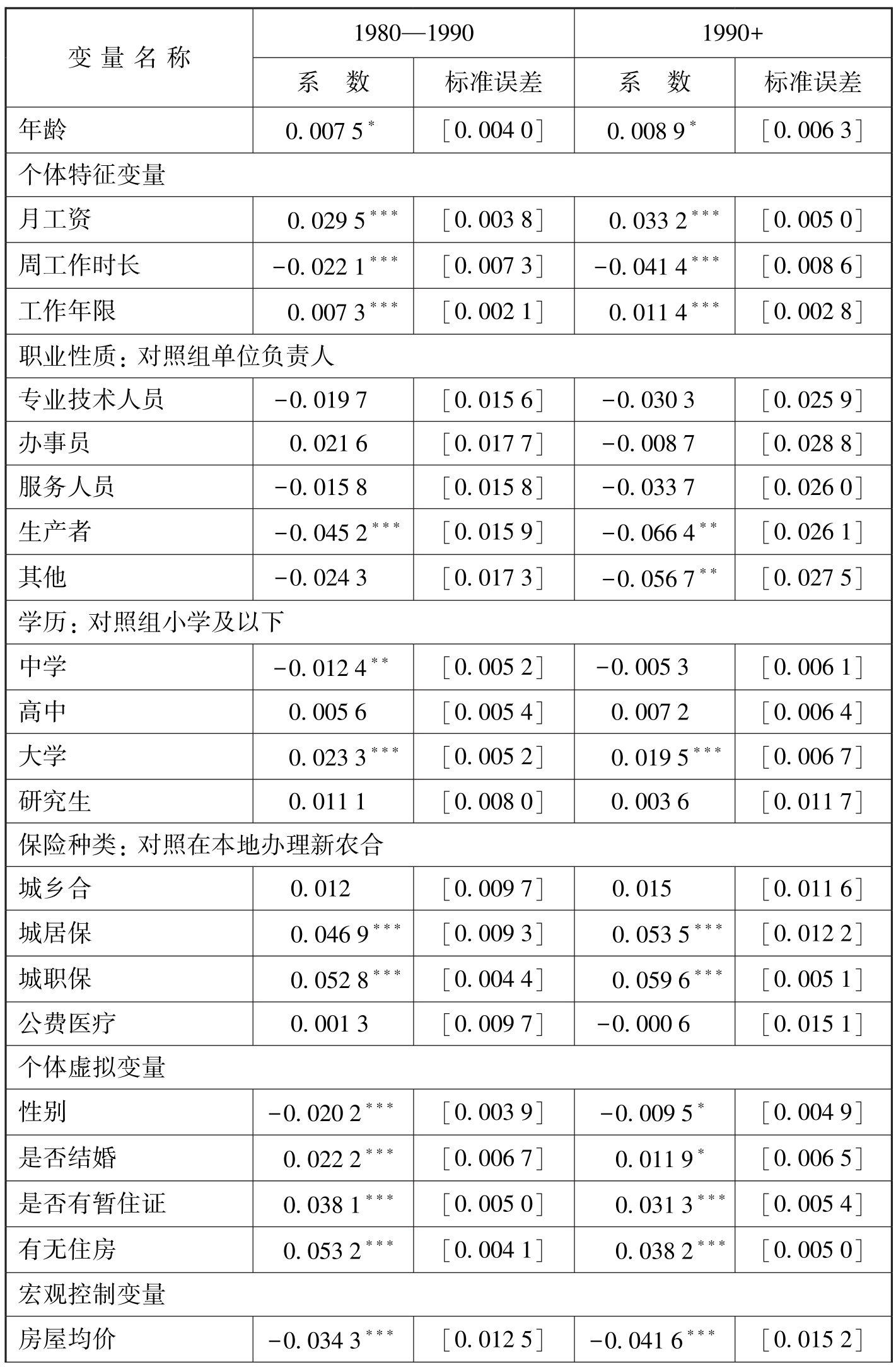
续 表

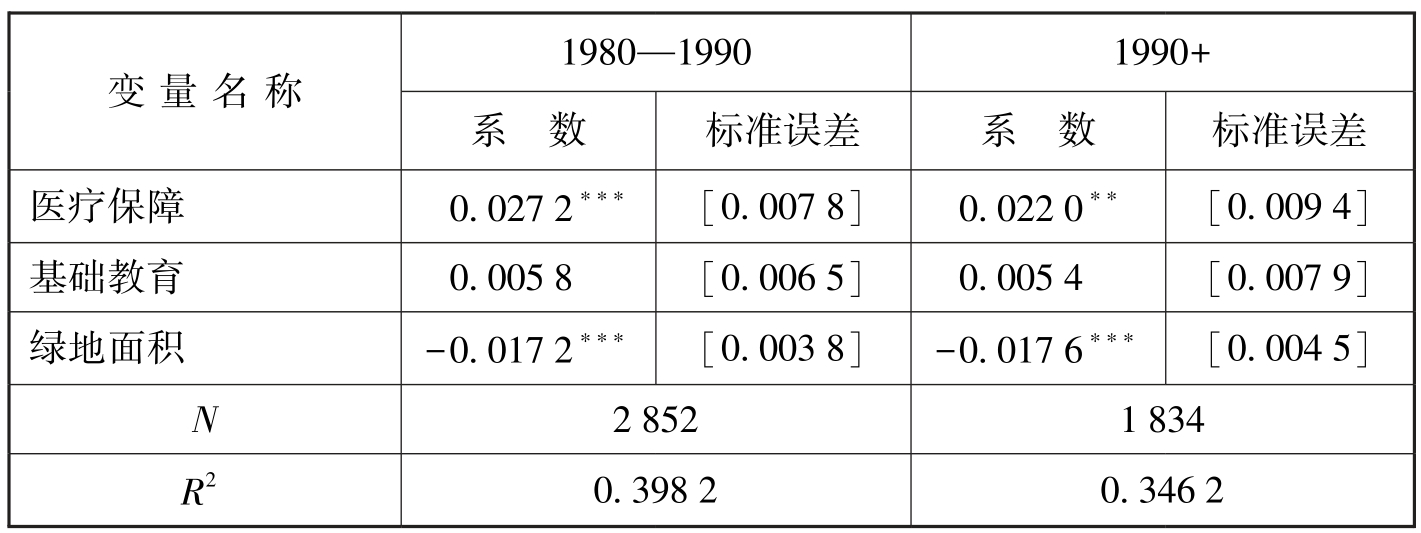
注： 括号中为p值，∗∗∗p<0.01，∗∗p<0.05，∗p<0.1。