2.3.2 海流运动方程
海水的各种运动都是在力的作用下产生的,其运动规律同其他物体的运动规律一样,遵循牛顿运动定律和质量守恒定律。为达到定量地研究海水运动规律,以下将简要地介绍一下海水的运动方程及求解方程的边界条件等。
所谓海水运动方程,实际上就是牛顿第二运动定律在海洋中的具体应用。单位质量海水的运动方程可以写成

式中 u——流速;
t——时间;
F——受到的外力。
只要给出作用力,便可由方程了解海水的运动状况。
作用在海水上的力有多种,归结起来可分为两大类:一类是引起海水运动的力,如重力、压强梯度力、风应力、引潮力等;另一类是由于海水运动后所派生出来的力,如地转偏向力(Coriolis force,亦称为科氏力)、摩擦力等。以下首先对海水所受各种力进行分析,并给出其解析表达式。
1)重力和重力位势
地球上任何物体都受重力的作用,当然海水也不例外。所谓重力是地心引力与地球自转所产生的惯性离心力的合力。习惯上人们将单位质量物体所受的重力称为重力加速度,以g表示。在海洋研究中,一般把g视为常量,取为9.80 m/s2。
对于静态的海洋,重力处处与海面垂直,此时的海面称为海平面。处处与重力垂直的面也称为水平面。从一个水平面逆重力方向移动单位物体到某一高度所做的功叫做重力位势,即
![]()
式中 dΦ——所做的功;
d z——物体铅直移动的距离。
位势相等的面称为等势面。静态海洋的表面是一个等势面。在海洋学中,两个等势面之间的位势差单位为gpm,其定义为
![]()
式中,g=9.80 m/s2,d z的单位为m。从上等势面向下计算的位势差称为位势深度。反之,从下等势面向上计算的位势差称位势高度。
由式(2-3)可见,两等势面的位势差,如果以gpm表示,则其量值恰与长度所表示的高度值相等,这在海洋学动力计算过程中是十分方便的。
2)压强梯度力
海洋中压力处处相等的面称为等压面。海洋学中把海面视为海压为零的等压面(以往称为一个大气压,大约为1013.25 hPa)。
在右手直角坐标系中,坐标原点取在海面,z轴向上为正,那么海面以下-z深度上的压力则为
![]()
式中 ρ——海水密度。
式(2-4)写成微分形式则有
![]()
在静态的海洋中,当海水密度为常数或只是深度的函数时,海洋中压力的变化也只是深度的函数,此时海洋中的等压面必然是水平的,即与等势面平行。这种压力场称为正压场。
根据牛顿运动定律,当海水静止时,水质点所受到的合力必然为零。但海水却总是处在重力的作用之下,且指向下方。由此可以推断,一定还存在一个与重力方向相反且与重力量值相等的力与其平衡。由式(2-5)知,该力为

它与压强梯度成比例,故称其为压强梯度力;与等压面垂直,且指向压力减小的方向,式中负号则表示与压强梯度的方向相反;1/ρ则表示计算的力是对单位质量而言的。图2-7a表示了正压场中压强梯度力与重力平衡的情况。当海水密度不为常数,特别在水平方向上存在明显差异(或者由于外部的原因)时,此时等压面相对于等势面将会发生倾斜,这种压力场称为斜压场,如图2-7b所示。
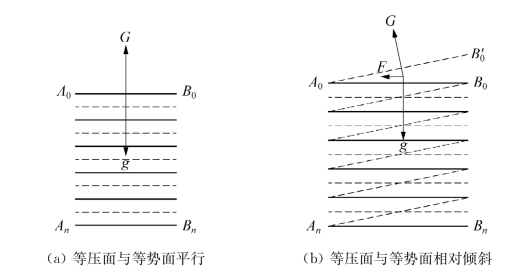
图2-7 等压面与等势面的关系
在斜压场的情况下,海水质点所受的重力与压强梯度力已不能平衡,由于等压面的倾斜方向是任意的,所以压强梯度力一般与重力方向不在同一直线上。其一般表达式为

式中 n——等压面的单位法向量。
因为海洋常常处在斜压状态,所以压强梯度力水平分量也就经常存在。尽管它的量级很小,但由于海水本身是流体,在水平方向上极小的力也会引起流动,它成了引起海水运动的重要作用力。
可以证明,海水质点所受的压强梯度力的广义定义就是单位质量海水所受静压力的合力。由式(2-5)知,两等压面之间的铅直距离为

显然它与海水密度成反比,说明在两等压面之间海水密度越大,则铅直距离越小;反之亦成立。因此,当海水密度在水平方向上存在明显差异时,必然导致两等压面之间的距离不等,使其相对于等势面而发生倾斜。这种由海洋中密度差异所形成的斜压状态,称为内压场。因为海洋上部的海水密度在水平方向上变化较大,而在大洋深处变化极小,甚至趋于均匀,因而由其决定的压力场,即内压场,在大洋上部的斜压性一般很强,随深度的增加斜压性逐渐变弱,到大洋某一深度处,等压面基本上与等势面平行,其水平压强梯度力也就不存在了。
此外,由于海洋外部原因,如海面上的风、降水、江河径流等因子引起海面倾斜所产生的压力场称为外压场。在外压场的作用下,等压面也可倾斜于等势面,因而也能使海水产生流动。外压场自海面到海底叠加在内压场之上,一起称为总压场。
3)地转偏向力
研究地球上海水或大气的大规模运动时,必须考虑地球自转效应,或称为科氏效应。人们把参考坐标取在固定的地表,由于地球不停地在以平均角速度ω=7.292×10-5 rad/s绕轴线自西向东自转,参考坐标系也在不断地旋转,因此它是一个非惯性系统。在研究海水运动时,必须引进由于地球自转所产生的惯性力,方能直接应用牛顿运动定律作为工具,从而阐明其运动规律。这个力即称为地转偏向力或科氏力。
由于地球自转所产生的惯性力是三维的。取x-y平面在海面上,x轴指向东为正,y轴指向北为正,z轴向上为正,科氏力的三个分量为
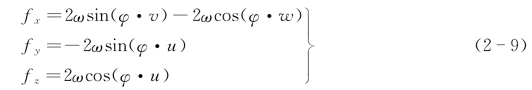
式中 ω——地球自转角速度。
在海洋中,由于海水的铅直运动分量w很小,故通常忽略与w有关的项,即简化为

式中,f=2ωsinφ,称为科氏参量,它是行星涡度的一种量度。
对海洋环流而言,科氏力与引起海水运动的一些力,如压强梯度力,相比量级相当,因此它是研究海洋环流时应考虑的基本力。
4)切应力
切应力是当两层流体作相对运动时,由于分子黏滞性,在其界面上产生的一种切向作用力。它与垂直两层流体界面方向上的速度梯度成正比,因此,当两层流体以相同的速度运动或处在静止状态时,是不会产生切应力的。单位面积上所产生的切应力为

式中 n——界面的单位法向量;
μ——分子黏滞系数,它的量值与流体的性质有关。
实际海洋中的海水运动总是处于湍流状态。由湍流运动所导致的运动学湍流应力比分子黏性引起的分子黏性应力大很多量级。在讨论海水运动时,将分子黏滞系数μ以湍流黏滞系数K代替。但μ与K的物理意义不同,μ只取决于海水的性质,K则与海水的湍流运动状态有关,其量级大于μ,且自身在各个方向的量值也有很大差异。
同时考虑海水在各方向的速度梯度,则单位质量海水所受应力合力的三个分量表达式可分别写为
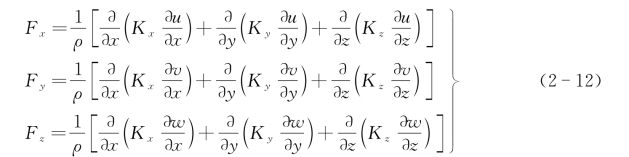
在海洋中,由于海水在水平方向的运动尺度比铅直方向上的大得多,所以水平方向上的湍流黏滞系数K x与K y比铅直方向上的K z也大得多。但鉴于海洋要素的水平梯度远小于铅直梯度,因此铅直方向上的湍流对海洋中的热量、动量及质量的交换起着更重要的作用。
海面上的风与海水之间的切应力,称为海面风应力,它能将大气动量输送给海水,是大气向海洋输送动量的重要方式之一。风应力目前只能以经验公式给出。
![]()
式中 ρa——海面以上空气的密度,一般取1.225 kg/m3;
W a——观测高度上的风速;
C a——阻尼系数(拖曳系数),它与海面上气流的运动状态有关。
在讨论海洋与大气之间的动量交换时,阻尼系数C a的确定常常因人而异。目前在数值计算中,只能依靠经验取值,不过在量级上差异不大。
5)引潮力及其他
引潮力是日、月等天体对地球的引力,以及它们之间作相对运动时所产生的其他力共同合成的一种力。它能引起海面的升降与海水在水平方向上的周期性流动。关于引潮力的确切定义、产生的机理及其解析表达式等,将在2.5节中介绍。
另外,引起海水运动的力还可以来自火山爆发和地震等。
以上分别讨论了海水运动所受的力及其表示形式,将它们分别代入式(2-1)中,则有
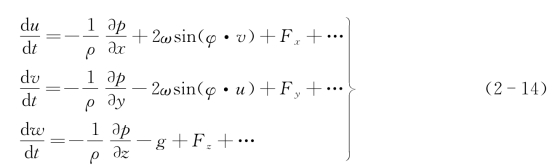
海水加速度=压力梯度力+科氏力+重力+切应力(海面风切应力和内部切应力),这就是海水运动方程的具体形式,在讨论海水的不同运动形式时,经常按实际情况对方程简化,以便求解。
此外,海流运动还要满足连续方程。所谓连续方程实质上是物理学中的质量守恒定律在流体中的应用,即流体在运动过程中,它的总质量既不会自行产生,也不会自行消失,由此导出连续方程:)

研究海洋环流时,通常考虑以下几种边界,一种是海岸与海底的固体边界,一种是与大气之间的流体边界,它们构成与海水之间的不连续面,因此,在运用运动方程和连续方程讨论海水的运动时,在边界上应附以边界条件。例如,在海岸与海底,由于它们的限制,海水垂直于边界的运动速度必然为零,至多只能存在与边界相切的速度。实际上,由于海水与海底的摩擦作用,离边界越近的海水运动速度应该越小,在边界上的运动速度理论上也应当为零。这些规定边界上海水运动速度所遵循的条件称为运动学边界条件。在大气和海洋交界面(海面)处的运动学边界条件为
![]()
式中 η——海面相对于平均海平面的起伏。
在海-气界面这一海面边界上,大气压力、风应力等直接作用于海面,然后通过海面影响下部海水。这些规定边界上海水受力所遵循的条件,称为动力学边界条件。另外,在研究局部海区的环流时,往往还需考虑与其毗连的海水侧向边界条件。
海水的真实运动规律是十分复杂的,实际工作中,人们往往采取各种近似或假定,对各种条件加以简化,从不同角度分别对海水运动情况进行讨论,从而阐明海水运动的基本规律。
