2.4.2 波浪理论简介
描述简单波浪运动的理论很多，其中最著名的理论有两个：一个是艾利（Airy，1845）提出的微幅波理论；另一个是斯托克斯（Stokes，1847）提出的有限振幅波理论。微幅波理论是基本的波浪理论，它较清晰地表达出波浪的运动特性，易于应用于实践，是研究其他较复杂的波浪理论及不规则波的基础。在数学上，微幅波理论可以看作是对波浪运动进行完整的理论描述的一阶近似值。对于某些情况，用有限振幅波理论来描述波浪运动会得到更加符合实际的结果。应该提到，第一个有限振幅波理论是Gerstner（1802）提出的，称为余摆线波理论，这一理论虽负有历史盛名，但由于它所描述的水质点运动并不符合实际观测的结果，而失去实用价值。斯托克斯提出的有限振幅波理论远较余摆线波理论优越，因而至今仍获得广泛的应用。
对于浅水区，Kortweg和De Vries（1895）提出了椭圆余弦波理论，它能很好地描述浅水条件下的波浪形态和运动特性。近年来许多学者根据这一理论编制出各种专门图表和计算程序，以便于应用。Rusell（1834）发现了孤立波的存在，这种波可视为椭圆余弦波的一种极限情况，在近岸浅水中，应用孤立波理论可获得满意的波浪运动的描述，因而亦被广泛应用。
随着计算机和计算技术的迅速发展，不少研究工作者提出了许多直接数值计算波理论。Dean（1965）提出了流函数波理论，这是一种类似高阶斯托克斯波理论的有限振幅非线性波理论。Reinercker和Fenton（1982）在流函数波理论的基础上，提出了一种傅里叶（Fourier）级数数值计算波理论，该理论不仅给出了便于工程上应用的各种波浪运动特性的表达式，而且适用于各种水深情况，对于波高较大的陡波，精度也较高。
在微幅波理论中，为了使问题简化，假设波动的振幅a远小于波长L或水深h，将非线性的水面边界条件作了线性化处理。如果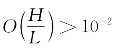
或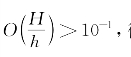
微幅波理论的误差较大。为此需要寻求更为精确的理论，这就是非线性的有限振幅波理论所要解决的问题。
有限振幅波包括斯托克斯波、椭圆余弦波和孤立波。有限振幅波的波面形状不是简单的余弦（或正弦）曲线，而是波峰较陡、波谷较坦的非对称曲线，这是由于非线性作用所致。非线性作用的重要程度取决于波高H、波长L及水深h的相互关系，具体来说取决于3个特征比值，即波陡δ=H/L、相对波高ε=H/h和相对水深h/L。在深水中，影响最大的特征比值是波陡δ，δ越大，非线性作用越大；在浅水中最重要的参数是相对波高ε，相对波高愈大，非线性作用愈大。
1）线性波理论
为把复杂的波动问题线性化，假设波高和波长（或水深）相比为无限小；水质点的运动速度较缓慢，速度的平方项和其他项相比可以忽略。在这些简化下，有关的流体力学方程组都成为线性的。这种简化的波浪理论称为微幅波理论、小振幅波理论或线性波理论。
（1）波面方程。现研究一列沿x方向以波速c向前传播的二维微幅波，如图2-12所示，x轴位于静水面上，z轴竖直向上为正。波浪在x-z平面内运动。
其波面方程式可以表示为
式中 η——波面距离静水面的高度；
a——波浪振幅。
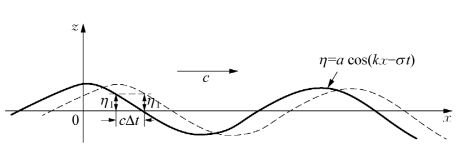
图2-12 微幅波传播示意图
式中，波数k=2π/L、圆频率σ=2π/T，式中σt前面采用正号或负号分别表示波浪沿正x方向或负x方向传播。
（2）速度势及色散关系。有限水深时微幅波势函数的表达式为
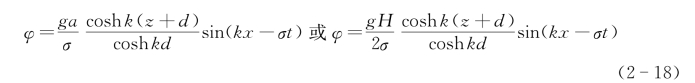
波速等于波长除以周期，即c=L/T或按c=L/T=σ/k。
因此，为了求得波速c，可从分析常数k和σ的关系入手，得到
式（2-19）称为色散关系。根据c=L/T可以得到与式（2-19）等价的波速和波长表达式
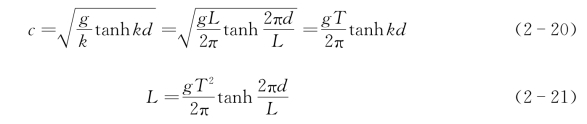
由式（2-20）可知，不同周期（波长）的波在传播过程中，由于波速不同将逐渐分散开来，这种现象称为波浪的色散现象，因此上述方程被称为波浪色散方程。
在深水和浅水条件下，波浪的弥散关系分别可以有近似表达式，见表2-3。
表2-3 波浪的分类
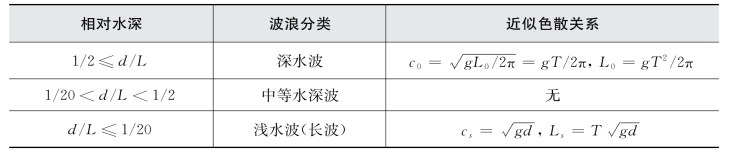
由表2-3中色散关系的深水和浅水近似可知，在深水情况下，波长和波速只与波周期有关，而与水深无关；在浅水情况下，波速变化只与水深有关，与波周期或波长无关。
（3）水质点运动的速度和加速度。流体内部任一点（x，z）处水质点运动的水平分速u和垂直分速w分别为
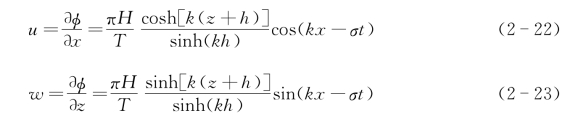
以z为变量的双曲函数cosh和sinh在水面处最大，海底处最小，因此水平和垂直分速沿水深以指数函数规律而减小。当相位ω=kx-σt=2nπ（n=0，1，2，…）时，发生最大的正水平速度；ω=（2n+1）π时，出现最大的负水平速度；ω=（2n+1/2）π时，出现最大的正垂直速度；ω=（2n+3/2）π时，出现最大的负垂直速度（图2-13）。
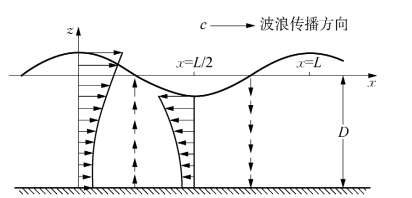
图2-13 微幅波质点运动速度在不同相位时的情况
流体内部任一点（x，z）处水质点运动的加速度可由下式求得
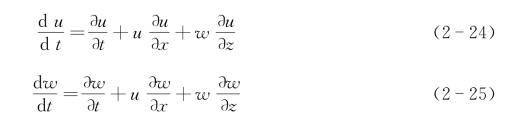
在微幅波理论中，可将流速场内由于各点速度不同而引起的加速度项，即式（2-24）和式（2-25）右边的第2、3两项略去，于是各点处水质点运动的加速度为
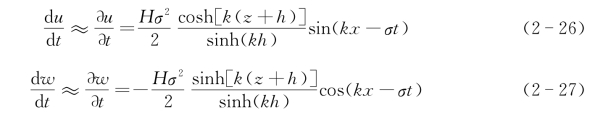
（4）波压力分布。微幅波场中任一点的波浪压力可由线性化的伯诺里方程求得，即
将式（2-18）代入式（2-28）得
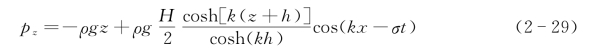
式（2-29）表明，波浪压力由两部分组成，等号右边第1项为静水压力部分，第2项为动水压力部分。波浪场静压和动压分布如图2-14所示。
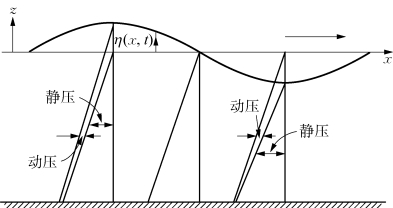
图2-14 微幅波的静压和动压分布图
（5）波能量。微幅波单宽波峰线长度一个波长范围内平均的波浪动能和势能相等，且都等于总波能的一半。单宽波峰线长度一个波长范围内的平均总波能，即单位海面面积上的总波能为
表明微幅波平均总波能与波高的平方成正比，其单位为焦耳/米2（J/m2）。
2）斯托克斯波浪理论
斯托克斯在1847年发表的论文把波浪运动的速度势函数用一个级数表示，然后将此级数在水面处展开使其满足非线性边界条件，得到了有限水深条件下的二阶近似解和无限深水的三阶近似解。1880年，斯托克斯又给出了有限水深的三阶近似解和无限深水五阶近似解。本书只简单介绍斯托克斯波理论的二阶近似解。
（1）速度势。
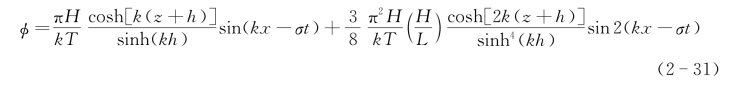
（2）波面高度。
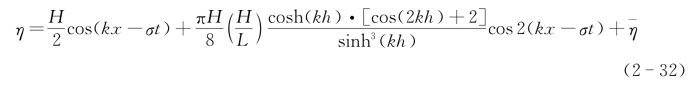
因此，斯托克斯二阶波的势函数和波面与线性波不同，分别增加了一个二阶项，但波长和波速却仍与线性波相同。
（3）水质点速度。
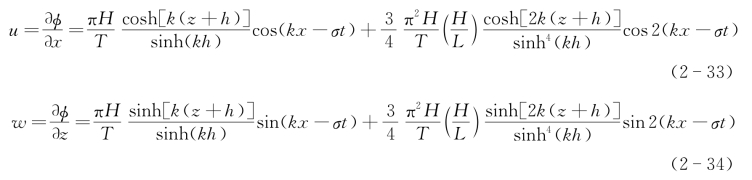
3）浅水非线性波理论
斯托克斯波不能适用水深很浅（如h＜0.125L）的情况，这时就应采用浅水非线性波理论。椭圆余弦波理论是最主要浅水非线性波理论之一，该理论首先由Kortweg和De Vries（1895）提出，其后由Keulegan、Patterson、Keller和Wiegel等人进一步研究并使之用于工程实践。在这一理论中波浪的各特性均以雅可比椭圆函数形式给出，因此命名为椭圆余弦波理论。典型的椭圆余弦波波面曲线如图2-15a所示。椭圆余弦波的一个极限情况是当波长无穷大时，趋近于孤立波（Solitary wave），其波面曲线如图2-15b所示。当振幅很小或相对水深h/H很大时，得到另一个椭圆余弦波的极限情况，称为浅水正弦波，其波面曲线如图2-15c所示。
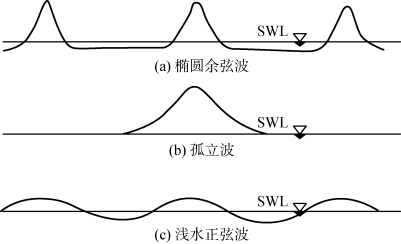
图2-15 椭圆余弦波及其两种极限情况的波面曲线
4）随机波浪理论
前面所叙述的都是在确定性意义上的规则波理论。实际的海洋波浪则是随机的，在一定的时间及地点，波浪的出现及其大小完全是任意的，预先无法确知，这种波浪称为随机波或不规则波。以波高为例，每次观测可测得一个确定的结果，但每次观测的结果彼此是不相同的，是随时间随机变化的。这种变化必须用随机函数，也叫随机过程，加以描述。
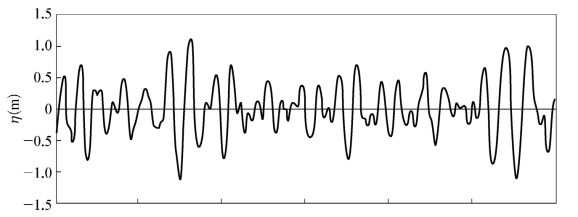
图2-16 海面波动的时间历程
不规则波系各波高值相差很大。那么如何描述这个波系的大小呢？一般有两种方法：一是特征波法，即对波高、周期等进行统计分析，采用有某种统计特征值的波作为代表波；二是谱方法。这里只讨论前一种描述方法。
对于特征波的定义，欧美国家多采用部分大波的平均值法，俄罗斯等国采用超值累积率法，我国则两者兼用。通常采用大约连续观测的100个波作为一个标准段进行统计分析。
（1）按部分大波平均值定义的特征波。
①最大波H max、T H max：波列中波高最大的波浪。
②十分之一大波H 1/10、T H 1/10：波列中各波浪按波高大小排列后，取前面1/10个波的平均波高和平均周期。
③有效波（三分之一大波）H 1/3、T H 1/3：按波高大小次序排列后，取前面1/3个波的平均波高和平均周期。
④平均波高¯H和平均波周期¯T：波列中所有波高的平均值和周期的平均值。
⑤均方根波高H rms定义为
这些特征波中最常用的是有效波，西方文献中泛指海浪的波高、周期时多指H 1/3和T H 1/3。
（2）按超值累积概率定义的特征波。
常用的有H 1%、H 5%、H 13%。以H 1%为例，其定义是指在波列中超过此波高的累积概率为1%。其他特征波的定义可以类推。
上述各特征值可由对实例资料进行统计分析予以确定，大波特征值和累积特征值可以相互转换，H 13%约相当于H 1/3，H 1/10约等于H 4%。
累积率波高H F%与平均波高¯H的关系，即
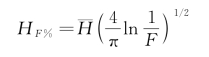
例如
常用部分大波的平均波高与平均波高关系为
