The CIP condition
Consider an investor who has initial capital, K, and faces two alternatives: (i)domestic investment, whereby the investor buys domestic assets, earning the domestic interest rate, i; and (ii)foreign investment, whereby the investor converts the domestic currency into foreign currency to buy foreign assets, earning the foreign interest rate, i*.Since domestic investment does not involve currency conversion, it does not involve foreign exchange risk (the risk arising from changes in the exchange rate).On the other hand, foreign investment produces exposure to foreign exchange risk, but this exposure can be covered by selling the foreign currency (buying the domestic currency)forward.Foreign exchange risk is eliminated because the forward exchange rate is known in advance, although it is used to settle transactions involving delivery of the currencies some time in the future.Thus, the investor knows in advance the domestic currency value of his or her foreign investment.If the position is not covered in the forward market, the investor has to wait until maturity and apply the spot exchange rate prevailing then to determine the domestic currency value of the foreign investment.
Suppose that we are considering a one-period investment starting with the acquisition of a financial asset (for example, a deposit)and ending with the maturity of this asset (see Figure 5.1).When the investor chooses domestic investment, the invested capital is compounded at the domestic interest rate and the investor ends up with the initial capital plus the interest income, that is K(1+i).If the investor chooses foreign investment, the initial capital is converted to foreign currency at the current spot exchange rate, obtaining K/S units of the foreign currency, where S is measured as domestic currency units per one unit of the foreign currency.If K/S worth of the foreign currency is invested in foreign assets, this capital is compounded for one period at the foreign interest rate such that the foreign currency value of the investment on maturity is (K/S)(1+i*).The domestic currency value of this investment is obtained by converting this amount into the domestic currency at the forward rate, F, to obtain (KF/S)(1+i*).
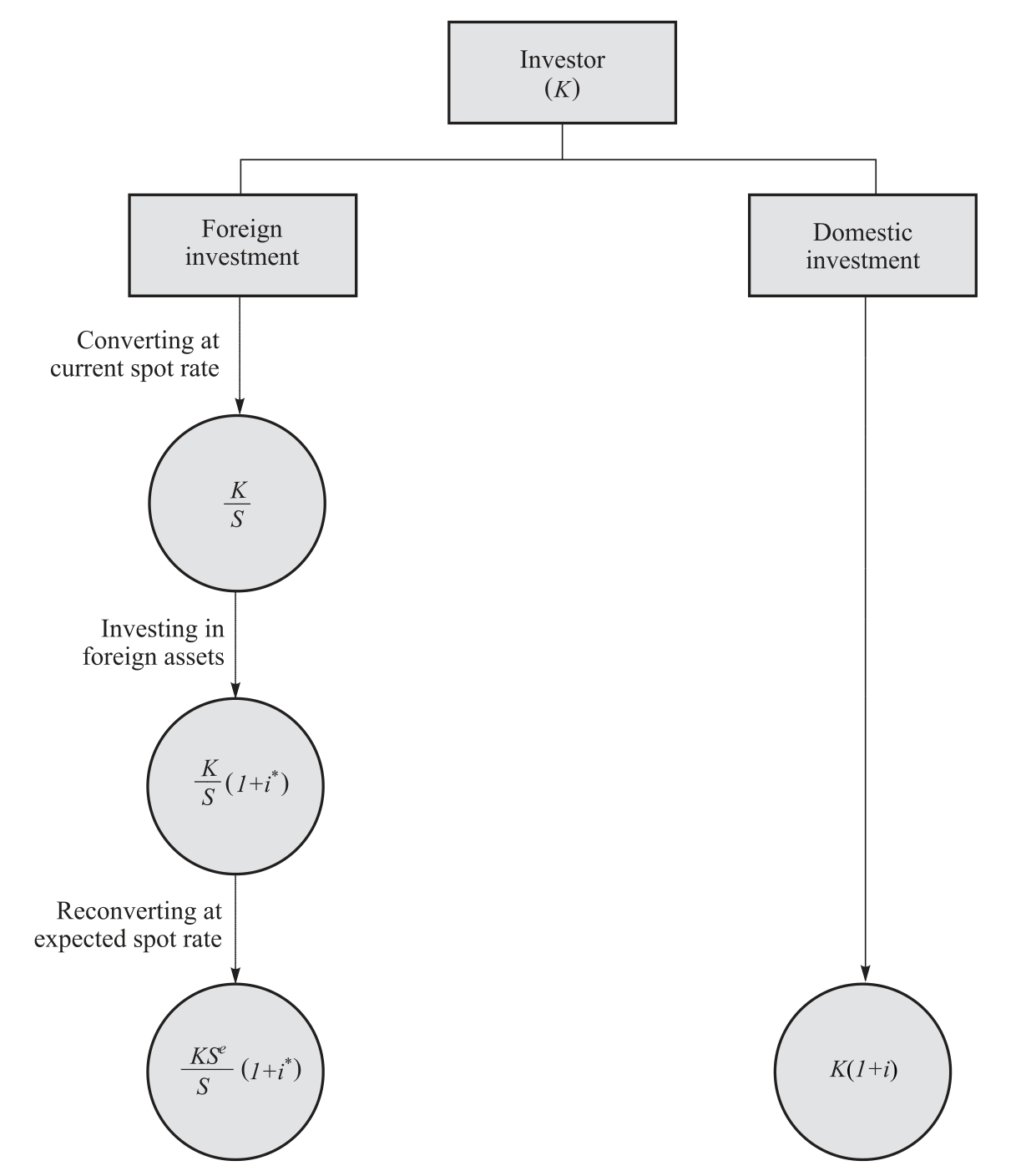
Figure 5.1 Return on domestic investment and foreign investment (with uncovered position)
Let us now assume that there are no restrictions on the movement of capital and that there are no transaction costs.We also assume that agents are risk-neutral, in the sense that they are indifferent between holding domestic and foreign assets if these assets offer equal returns.The equilibrium condition that precludes the possibility of profitable arbitrage is that the two investments must be equally profitable, in the sense that they provide the same domestic currency amount of capital plus interest.Hence

By expressing the condition in terms of one unit of the domestic currency, we obtain

This equilibrium condition tells us that gross domestic return is equal to gross covered foreign return.The left-hand side of Equation (5.11)is the gross domestic return: it is “gross” because it includes the amount invested (one unit of the domestic currency)and the interest earned, i.
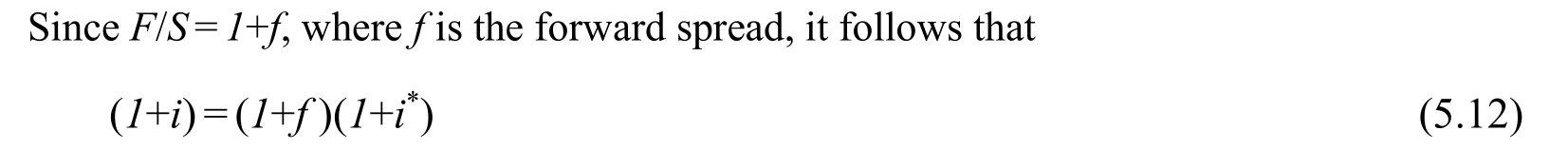
By simplifying Equation (5.12), ignoring the term f (because it is numerically negligible), we obtain the approximate CIP condition
which tells us that in equilibrium the interest differential must be equal to the forward spread.Equation (5.13)implies that the currency offering the higher interest rate must sell at a forward discount, and vice versa.This is because if i > i*, then f > 0, which means that the foreign currency (offering a lower interest rate)sells at a forward premium whereas the domestic currency (offering a higher interest rate)sells at a forward discount.On the other hand, if i < i*, then f < 0, implying that the foreign currency sells at a discount while the domestic currency sells at a premium.
