The spot exchange market
Spot quotations
● Direct dollar quotes
Most financial centers quote the number of units of domestic currency for one unit of foreign currency.Thus, in the euro-zone the spot exchange rate between the dollar and the euro will be quoted:
which means that it takes EUR 1.1 to buy USD1.In Switzerland the spot exchange rate will be quoted:
which means it takes CHF 2 to buy USD1.If we want to know how many dollars it takes to buy one euro or one Swiss franc, we simply take the reciprocal of the dollar rate:
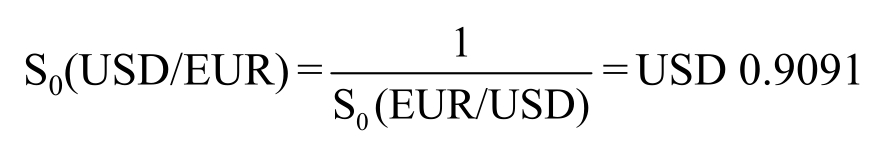
which means it takes 90.91 US cents to buy one euro and
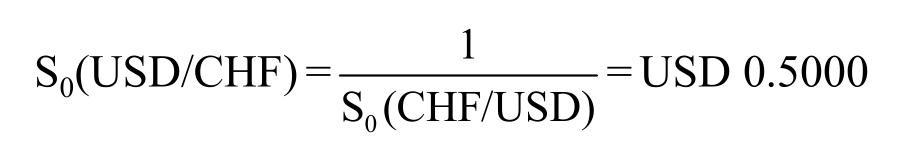
which means it takes 50 US cents to buy one Swiss franc.
Unfortunately all countries do not respect this convention.In the United Kingdom and Ireland, among others, quotes are made in the number of units of foreign currency it takes to buy one unit of domestic currency.Starting in 1979 New York banks also went on what is called European terms, which involves giving the number of units of foreign currency it takes to buy one dollar.American terms refer to giving the number of dollars it takes to buy one unit of foreign currency.French-speaking countries call quotes in the number of units of domestic currency for one unit of foreign currency as the “in-certain” and quotes in the number of units of foreign currency for one unit of domestic currency as the “certain”.In any case, what is important is to know which currency is in the denominator because the currency in the denominator is the unit currency.You will have noticed that our notation, although somewhat cumbersome, makes that clear.When reading foreign currency tables, however, you must take care to avoid errors.
The rates set out in Table 6.1 are inter-bank rates and the column labeled “Closing midpoint” refers to the spot rate taken towards the end of London trading.Notice in the column labeled “Bid/offer spread” that there are two rates for each currency.The first rate refers to the bid rate and the second to the ask rate.Banks were willing, for example, to buy dollars and pay CHF 1.6374 per dollar.On the other hand, they would sell dollars and charge CHF 1.6380 per dollar.The difference is the spread and it represents the banks’ gain.In this case we can see that it is very small, at less than 0.04%.
Table 6.1 Selected US dollar spot and forward rates, 27 December 2000
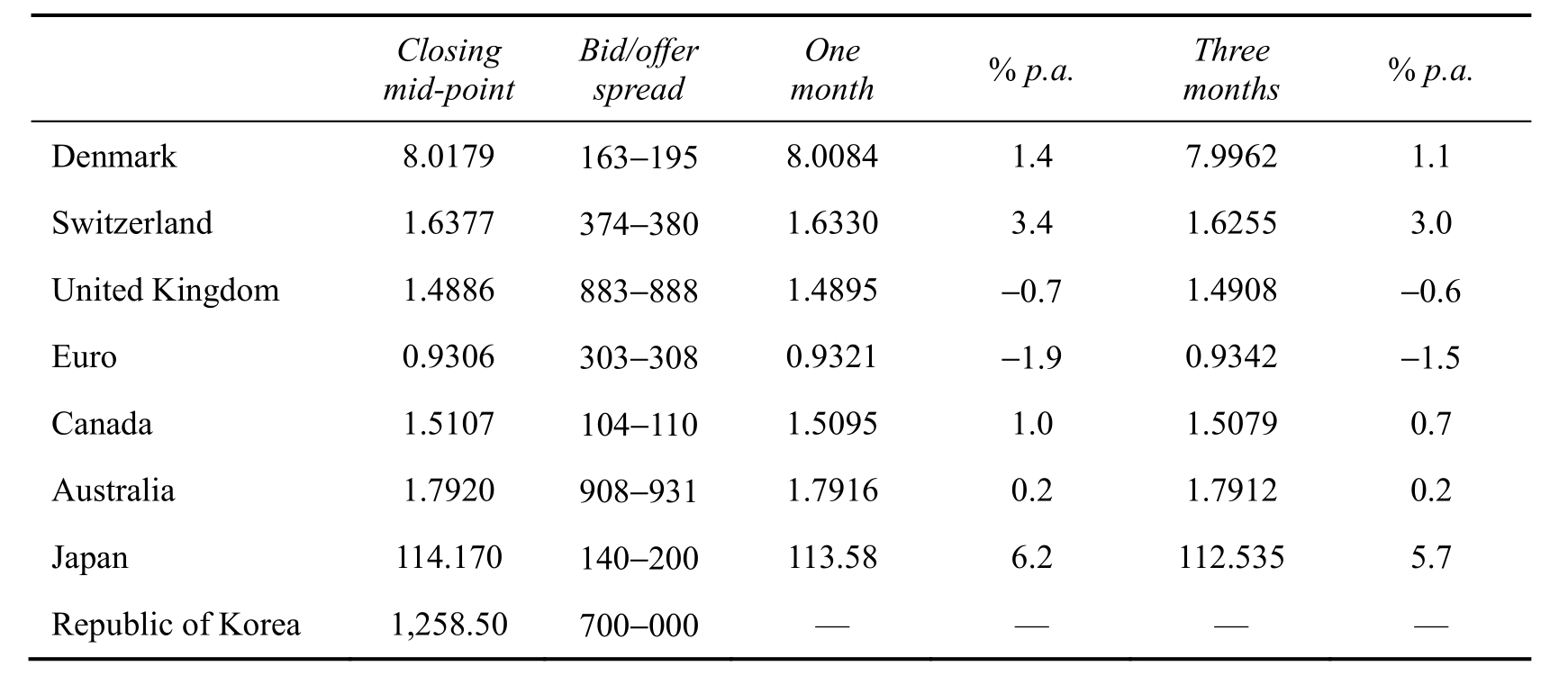
Note: Bid/offer spreads in the dollar spot column show only the last three decimal places.The UK pound and the Euro are quoted in US currency.
Source: Financial Times.
Spreads make it a little more complicated when going from European to American quotes or from the “certain” to the “uncertain” by taking the reciprocal as we did above.Just remember that foreign exchange quotes are symmetrical.Buying one is the same as selling the other.For example, buying dollars for Swiss francs is the same as selling Swiss francs for dollars.Hence, the reciprocal of the bid price for dollars is the ask price for francs:
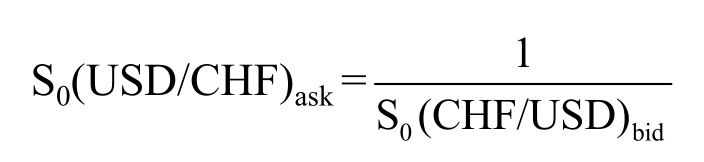
By the same token, selling dollars for francs is the same thing as buying francs for dollars.Therefore, the reciprocal of the ask price for dollars is the bid price for francs:
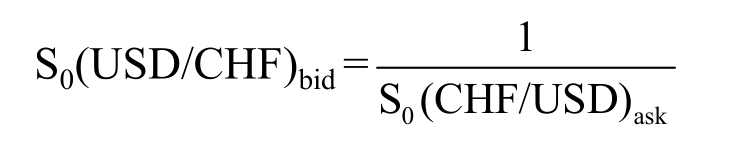
We can use these two formulae to calculate the bid-ask dollar rates on the Swiss franc from the information in Table 6.2.
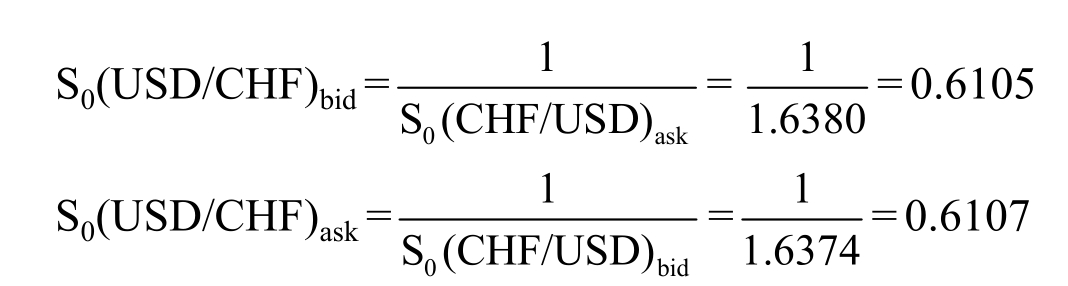
Thus, the bid-ask dollar rates on the Swiss franc would be 0.6105-0.6107.
One last remark is in order.Professional traders have a shorthand way of quoting prices.Rather than quote the rate as 0.6105-0.6107, or even 0.6105-07, they will only quote the last two digits, 05-07.For non-traders quotes like this seem somewhat mysterious.However, because traders follow the market continuously, they know what the missing figures are.Just to make sure that there is no confusion, we shall continue to give the full quote.
● Cross rates
For currencies that are traded frequently like the US dollar, the Swiss franc and the Japanese yen, the system is fairly straightforward.But what about the rate of the Vanuatuvatu (VUV)for the Vietnamese dong (VND), or the Malawi kwacha (MWK)for the Maldivian rufiyaa (MVR)? The IMF records exchange rates for 152 countries, which means that there are (152×151)÷2 = 11,476 different pairs of currencies and the same number of possible exchange rates.Most of these possibilities are likely never to come up for a trade and many only once in a blue moon.If they do come up, however, how can the trader arrive at a price?
The answer is that all currencies are quoted against the US dollar.Knowing the price of any two currencies against the dollar means that the price of one currency for the other can easily be found.The exchange rate between two currencies not involving the dollar is called the cross rate.
Let’s forget about the spread for a moment and take a simple example.Suppose the following information is available:
S0(CHF/USD)= CHF 2.0000
S0(JPY/USD)= JPY 120.0000
The number of Japanese yen for Swiss francs or the number of francs for yen can easily be found.If you had yen and wanted francs, you could pay JPY120 and get USD1.Then you could sell the dollar and buy CHF 2.For each franc you would have paid JPY 120/CHF 2= JPY 60.If you had Swiss francs and wanted yen, you could sell CHF 2 first and receive USD1.Then you could sell the dollar and buy JPY 120.For each yen you would have paid CHF 2/ JPY 120 = CHF 0.0167.
Suppose, then, that you have USD 1 million and the following information:
In New York USD1 = CHF 2.0000
In London USD1 = JPY 120.000
In Tokyo CHF1 = JPY 59.000
Something is wrong in Tokyo.You know that the JPY/CHF rate should be JPY 60 but it is only 59.As an astute trader, you could sell your dollars and buy JPY 120 million in London.You could sell your yen for CHF 2,033,898 in Tokyo and then use them to buy USD 1,016,949 in New York, making a profit of USD 16,949.This is called “triangular arbitrage”, which in an efficient market should keep the exchange rates from getting out of line.Buying yen in London would raise the price of yen for dollars.Selling yen in Tokyo would lower the price of yen for Swiss francs and buying dollars in New York would lower the price of francs for dollars.This would continue until the arbitrage opportunity disappeared.In today’s world of sophisticated telecommunications and round-the-clock trading, arbitrage opportunities such as this should be short-lived.
When spreads are involved, the reasoning is the same but the calculations are a little more complicated.Suppose you are a trader and you are asked for a quote on Philippine pesos for the Australian dollar.This is a combination that you don’t see too often and is not being quoted directly.Therefore, you get the quotes of pesos for dollars and AUD for dollars, which are:
Philippine peso (PHP): 49.9000-50.0000
Australian dollar: 6.8475-6.8525
You then make the following argument.If my client wants to buy pesos, he could obtain pesos for AUD by first buying dollars and paying NOK 6.8525 and then selling the dollars and receiving PHP 49.90.The price per AUD would then be 49.90/6.8525 = PHP 7.2820 per AUD.My bid price can’t be any lower than this, otherwise my client will by-pass me and take this route.On the other hand, if he wants AUD my client could obtain AUD for pesos by buying dollars with pesos for PHP 50.00 per dollar and then selling the dollars for AUD 6.8475.The price of each AUD will then be 50.00/6.8475 = PHP7.3019 per AUD.My ask price cannot be any higher than this otherwise my client will by-pass me and take this route.Thus my direct quote has to be somewhere between the limits of:
So (PHP/AUD): 7.2820-7.3019
The reason that it could be somewhere between the two limit quotes is that calculating the cross rate from the bid-ask price effectively includes the transaction cost of buying and selling against the dollar.Some banks may want to buy or already be holding pesos or AUD or both, and thus be willing to reduce their spread.Consequently, a better situation than the limit quotes is likely to exist, especially with a bank that is a market-maker in the direct exchange under consideration.When dealing in cross rates, it will probably pay to shop around for a price better than the limit quotes.
Arbitrage within the spot exchange market
We have pictured foreign exchange as a single market for trading between two currencies.Yet we have also noted that trading occurs in different locations around the world.For instance, for a period of time each day, trading is occurring in both New York and London as well as in other money centers in Europe.Will the rates in the different locations be essentially the same at a point in time, or can they diverge as local supply and demand conditions differ? Furthermore, exchange rates exist for many different currencies, both rates representing the dollar price of various foreign currencies and the cross-rates between foreign currencies.Are these exchange rates and cross-rates related in some way, or can they have independent levels?
Arbitrage, the process of buying and selling to make a (nearly)riskless pure profit, ensures that rates in different locations are essentially the same, and that rates and cross-rates are related and consistent among themselves.What would happen if pounds were being exchanged at $1.70 per pound in London, and $1.60 per pound at the same time in New York? If foreign exchange trading and money transfers can be done freely, then there is an opportunity to make a riskless profit by arbitraging between the two locations.Buy pounds where they are cheap (in New York)and simultaneously sell them where they are expensive (in London).For each pound bought and sold at the initial exchange rates, the arbitrage profit is 10 cents.Such arbitrage would occur on a large scale, increasing the demand for pounds in New York and increasing the supply of pounds in London.The dollar-pound exchange rate then would increase in New York and/or decrease in London, and the two rates would be driven to be essentially the same (that is, within the small range reflecting transactions costs that prevent any further profitable arbitrage).
What would happen if the exchange rate for the pound in terms of dollars is $1.60, the exchange rate for the Swiss franc in terms of dollars is $0.50, and the cross-rate between the franc and the pound is 3 franc per pound? Although it is more subtle, there is also an opportunity to make a riskless profit by arbitrage through the three rates—a process called triangular arbitrage.To see this, start with some number of dollars, say $150.Your $150 buys 300 francs (100/0.50).Use these francs to buy pounds at the cross-rate, and you have 100 pounds (300/3).Convert these pounds back into dollars and you end up with $160 (100×1.60).Your triangular arbitrage has made $10 profit for each $150 you start with.This profit occurs almost instantly and with essentially no risk if you establish all three spot trades at the same time.
As a large amount of this triangular arbitrage occurs, pressures are placed on the exchange rates to bring them into line with each other.The extra demand for francs tends to increase the dollar-franc exchange-rate.The extra demand for pounds (paid for by francs)tends to increase the franc-pound cross-rate.The extra supply of pounds (to acquire dollars)tends to reduce the dollar-pound exchange-rate.One or more of the exchange rates will change (due to demand and supply pressures)so that the cross-rate of francs per pound essentially equals the ratio of the dollar-pound exchange rate to the dollar-franc exchange rate.For instance, if only the cross-rate changes, then its value must shift to 3.2 francs per pound (1.60/0.50).At this cross-rate there is no further opportunity for profits from triangular arbitrage.
Just the threat of arbitrage of these types usually keeps the exchange rate between two currencies essentially the same in different locations, and keeps cross-rates in correct alignment with other exchange rates.Opportunities for actual arbitrage of these types are rare.
