The mechanics of covered arbitrage
Covered interest arbitrage consists of going short on (borrowing)one currency and long on (investing in)another currency, while covering the long position via a forward contract (selling the currency forward).Upon the maturity of the investment (and the forward contract)the proceeds are converted at the forward rate and used to repay the loan (covering the short position).The difference between the proceeds from the investment and the loan repayment (principal plus interest)is net arbitrage profit or the covered margin.For arbitrage to be profitable the covered margin must be positive.This process is illustrated in Figure 5.2.
Arbitrage from the domestic currency to a foreign currency
Arbitrage in this case consists of the following steps:
1.The arbitrager borrows domestic currency funds at the domestic interest rate, i.For simplicity, we assume that the amount borrowed is one domestic currency unit.
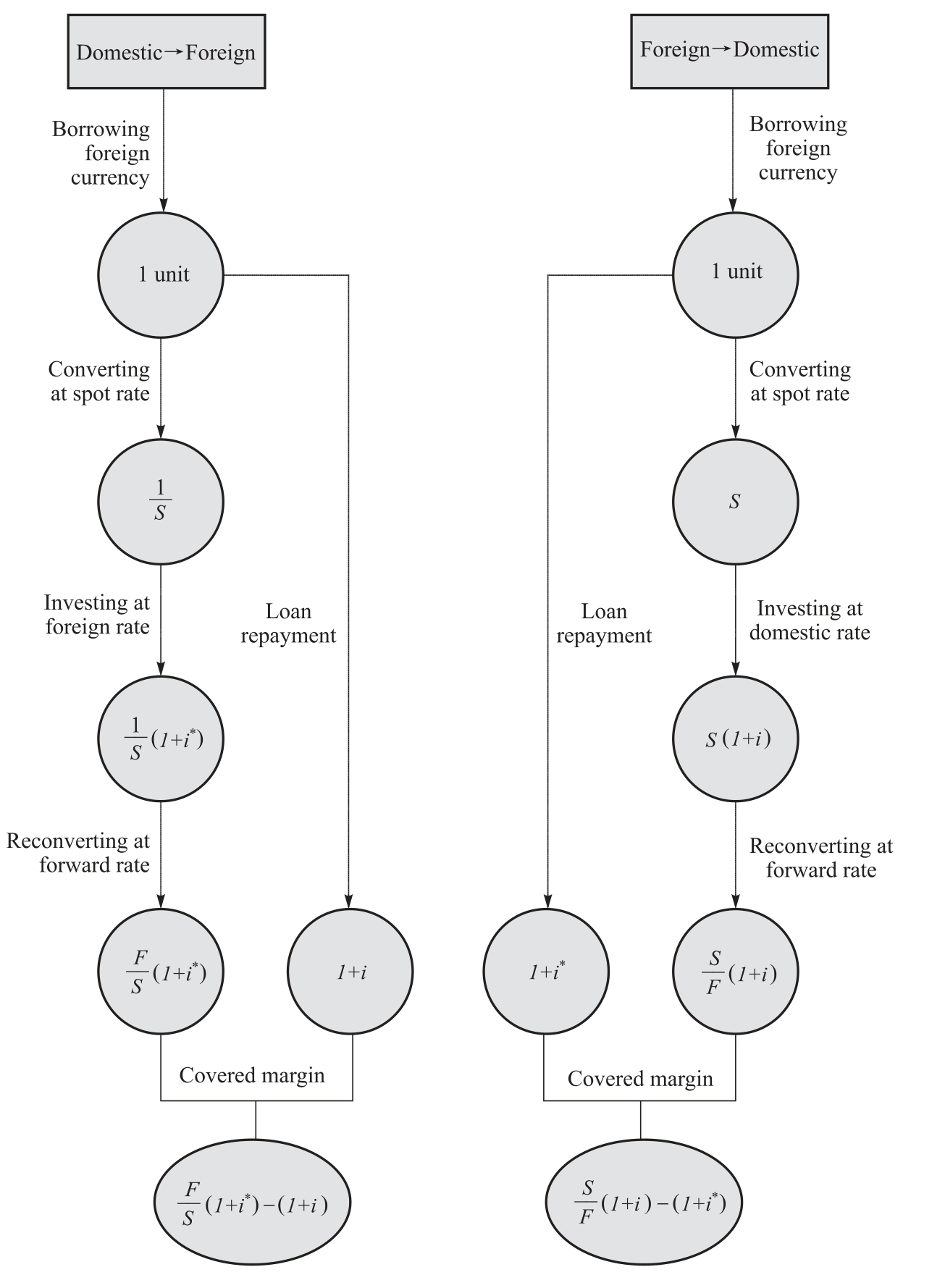
Figure 5.2 Covered interest arbitrage
2.The borrowed funds are converted at the spot exchange rate, S, obtaining 1/S foreign currency units.This amount is invested at the foreign interest rate, i*.
3.The foreign currency value of the invested amount at the end of the investment period is (1/S)(1+i*).
4.This amount is reconverted into the domestic currency at the forward rate, F, to obtain (F/S)(1+i*)domestic currency units.
5.The value of the loan plus interest is (1+i)domestic currency units.
The covered margin, π, is the difference between the domestic currency value of the proceeds and the loan repayment, which gives

or approximately
Equation (5.15)tells us that the covered margin on arbitrage from the domestic to a foreign currency consists of the interest rate differential (foreign less domestic)and the forward spread.
Arbitrage from a foreign currency to the domestic currency
Arbitrage in this case consists of the following steps:
1.The arbitrage borrows foreign currency funds at the foreign interest rate, i*.For simplicity we again assume that the amount borrowed is one foreign currency unit.
2.The borrowed funds are converted at the spot exchange rate, S, obtaining S domestic currency units.This amount is invested at the domestic interest rate, i.
3.The domestic currency value of the invested amount at the end of the investment period is S(1+i).
4.This amount is reconverted into the foreign currency at the forward rate, F, to obtain (S/F)(1+t)foreign currency units.
5.The value of the loan plus interest is (1+i*)foreign currency units.
The covered margin is again the difference between the foreign currency value of the proceeds and the loan repayment, which gives

or approximately
Equation (5.17)tells us that the covered margin on arbitrage from a foreign to the domestic currency consists of the interest rate differential (domestic less foreign)and the negative of the forward spread.
The no-arbitrage condition
The no-arbitrage condition is obtained when the covered margin is zero.By substituting in Equation (5.14)or (5.16), we obtain

Where F is the interest parity forward rate, which is the value of the forward rate that is consistent with the no-arbitrage condition.If CIP holds, then F= F (that is, the interest parity forward rate is equal to the actual forward rate).
Suppose that you approach your banker, requesting a quote for the forward rate between the domestic currency and foreign currency, perhaps because you want to buy the foreign currency forward to cover future payables.The banker may not know what CIP is, but will search in a manual for a formula that provides an expression for the forward rate.This formula would look like Equation (5.18).Why would the banker use this formula to calculate the forward rate? Simply because if the banker chose any other forward rate, you could make (riskless)profit out of your banker by indulging covered arbitrage.
