7.2.4 降雨径流关系
降雨径流关系是水文实践中推求产流量常用的一种方法。在水文水资源分析计算和水文情报预报中,为了推求一定降雨量所产生的径流量,必须建立降雨量与产流量,以及与其他影响因素之间的关系。一般常用的有降雨径流经验相关图与降雨径流模型两种途径。
1.蓄满产流模式的降雨径流关系
(1)降雨径流相关图。根据形成一次洪水的降雨量和相应径流量所建立的降雨径流相关关系,简称为次降雨径流关系。以此类推,根据月、季、年的降雨与相应径流量建立的降雨径流关系,分别称为月、季和年的降雨径流关系。至于如何建立降雨径流相关图将在水文情报预报课程中介绍,下面仅介绍次降雨径流关系的有关规律和特性。
以蓄满产流为主的地区,影响产流量大小的因素为降雨量和初始土壤含水量,即
![]()
式中 R——产流量,mm;
P——降雨量,mm;
W0——降雨开始时刻的流域平均土壤含水率,mm。
就整个流域而言,W0很难用实测土壤含水量值来表示,在建立经验相关图时,常用反映前期流域土壤含水量大小的指标Pa来表示,Pa又称为前期影响雨量。它可根据前期的降雨和蒸发来间接推算,至于推算的具体方法也将在水文情报预报中作详细介绍。相关图的形式如图7.11所示。其中,图7.11(a)为以Pa为参数的形式,即R=f(P,Pa);图7.11(b)为R=f(P+Pa)形式。
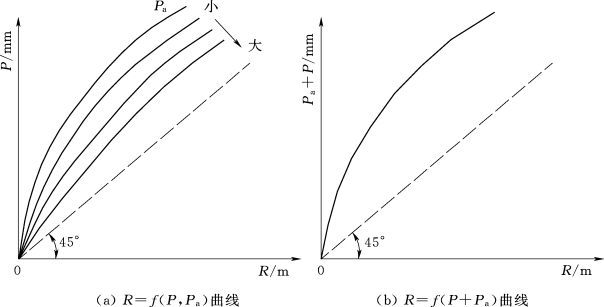
图7.11 蓄满产流的降雨径流相关图
此类相关图应用起来比较方便,可以由P、Pa直接查算出R,进而根据降雨过程求得产流量过程。但是它仅在湿润地区和半湿润地区使用才有较好效果。因为在这些地区,地下水埋藏较浅,前期土壤缺水量不大,一次降雨很容易使包气带饱和,其产流量大小主要取决于降雨量的大小和土壤初始缺水量的大小,而与降雨强度的变化关系不大。
降雨径流经验相关图,是根据实测的雨洪资料并考虑一些主要影响因素建立的相关关系,虽然在水文水资源分析计算和水文情报预报中有一定的实用价值,但是它缺乏物理基础,难以揭示产流过程中各要素的成因关系,所以其应用特别是外延时受到限制。如果以产流过程的物理概念为基础,探求产流各因素之间的数学关系,从而建立降雨径流关系的数学模型,则称为产流模型。当掌握了产流过程的理论概念以后,完全有可能从理论的角度来探求这种关系的基本形式,流域蓄水容量面积分配曲线和下渗能力面积分配曲线是建立降雨径流关系的理论基础。
(2)蓄满产流计算模型。用特定数学方程描述流域蓄水容量面积分配曲线,如抛物线方程或指数方程,对于任一给定的降水量P和已知初始土壤含水率W0,可依据图7.7和图7.8所示的面积关系,用积分的方法求得相应的径流量R。当雨前流域平均初始蓄水量W0=0时,对于特定降雨量P,可按上述方法求得相应的R,从而可获得一条以W0=0为参数的P-R关系曲线,如图7.12所示。若流域平均初始蓄水量W0=W1,对于特定降雨量P,可利用蓄水容量面积分配曲线,采用上述同样的方法,也可求得相应的R,从而得到一条以W1为参数的P-R关系曲线,以此类推,可建立W0=W1,W2,W3,…时的P-R关系曲线簇,如图7.12(b)所示。
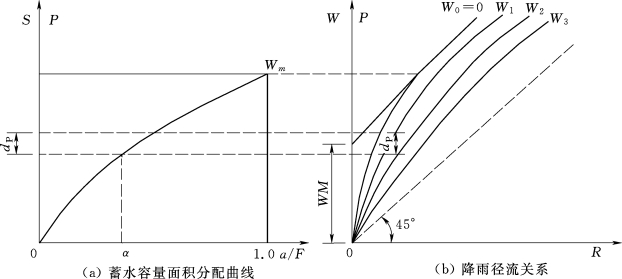
图7.12 蓄水容量面积分配曲线与降雨径流关系
由流域蓄水容量面积分配曲线的概念可知,曲线的上部为平行于P=R(即45°线)的直线,相当于全流域产流的情况,如雨前初始流域蓄水量为W0,全流域最大蓄水量为WM,当全流域都产流时,有
![]()
这表明,当全流域产流时,其产流量与蓄水容量面积分配曲线的线型无关,仅取决于流域的缺水量(WM-W0)。若雨前W0=0,全流域产流时的产流量为R=P-WM,因此,对于W0=0的P-R关系曲线,其上部直线部分向下的延长线在纵轴上的截距即为WM。关系线的下部为曲线,相当于流域部分产流的情况,在这一范围内,产流量除了与降雨量有关以外,还与蓄水容量面积分配曲线的线型有关。如降雨开始,全流域已蓄满,即W0=WM时,R=P,它是一条通过原点的45°的直线。从图7.12中可以看出,W0=0和W0=WM对应的两条线的上部的水平距离为WM,因为对于W0=0时,曲线上部的方程为R=P-WM,而W0=WM时的方程为R=P,也就是W0=0时曲线的上部是由R=P线向左平移WM得到的。
利用蓄水容量面积分配曲线,还可以说明一个重要的概念,即相对产流面积等于径流系数。设对应于某一W0值,产流面积为(a/F),若有降雨增量d P,其产流量为d R,由图7.12可见,d R=d P(a/F),故得
![]()
也就是蓄满产流的径流系数等于其产流面积的相对值。而由P-R关系曲线可知,(d R/d P)为P-R关系曲线上某点斜率的倒数,即
![]()
式(7.16)表明,降雨径流关系曲线上任一点的斜率的倒数,等于在该点处的径流系数。由图7.12可见,曲线的下部,其切线的倾角θ>45°,即tanθ>1,所以径流系数α<1,并且越向上,由于斜率越小,所以径流系数越大,而在上部直线部分,θ=45°,径流系数α=1,表示已达到全流域产流。
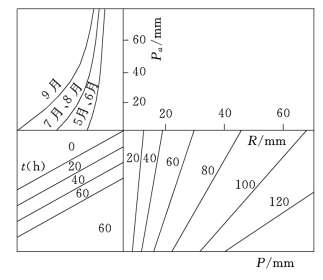
图7.13 五变量合轴降雨径流相关图
上面所介绍的降雨径流模型有两个待定参数,一般可通过实测降雨、径流资料率定。这些参数一旦确定,上述降雨径流关系即可确定。
2.超渗地面径流产流的降雨径流关系
(1)降雨径流相关图。超渗地面径流的产流量,除了与当时的土壤含水量有关以外,还与降雨强度有关。所以其降雨径流相关图,需要加入反映雨强的参数,实际工作中常以一次暴雨的历时或有效历时表征该次暴雨的平均雨强。图7.13为五变量合轴降雨径流相关图,其关系可表达为R=f(P,Pa,t,月份),Pa为前期影响雨量,t为暴雨历时用于表征该次降雨的平均强度。但是实践证明,对于超渗地面径流产流类型,该相关图应用效果不好。原因在于,超渗产流的产流量主要取决于降雨过程中下渗强度与降雨强度的对比,而下渗强度受到很多随机因素的影响,相关图很难全面反映这些因素,所以这种相关图往往精度较差。
(2)下渗曲线法与超渗产流计算模型。超渗产流计算的基本依据是建立流域下渗能力与土壤含水量之间的关系,常称为下渗-储量关系,即(https://www.daowen.com)
![]()
式中 fp——下渗能力,mm/h或mm/min;
W——土壤含水量,mm。
建立了f-W关系后,只要知道雨初土壤含水量W0,根据各时段雨量Pi,就可以推求出各时段产流量Rsi。
当Pi≤fpΔt,则 ![]()
当Pi>fpΔt,则 ![]()
式中 fp——时段平均下渗能力,由时段土壤含水量Wi确定,mm/h或mm/min;
ΔW——时段土壤含水量的增量,mm;
Δt——计算时段长,h或min。
由此可见,超渗产流计算,关键在于确定fp-W关系。如果已知流域的下渗能力曲线fp-t,则可以由下式转换为fp-W关系,即

式中 Wt——t时刻的土壤含水量。
式(7.20)表明,若自供水开始时刻(t=0)起,给定不同的时刻t,计算其累积下渗量Wt,就可建立fp-W关系,其转换关系如图7.14所示。
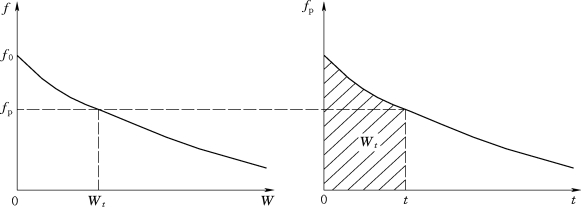
图7.14 ft-W与ft-t间的转换关系示意图
下渗能力曲线fp-t的确定,目前常用的有水文分析法及下渗模型法两种途径。水文分析法是根据实测的降雨过程和流量过程,求得fp-W关系和fp-t关系;下渗模型法是应用下渗公式中fp-t的函数关系,再由式(7.20)转换为fp-W关系。常用的下渗公式为
霍顿公式 ![]()
菲利普公式 ![]()
为便于计算,可将其转换为fp-W关系,对于霍顿公式
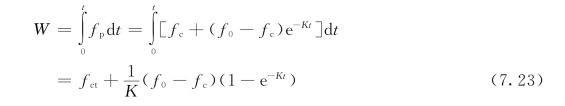
与式(7.21)联立,消去t,得
![]()
从上述式子可以看出,下渗模型有3个待定参数:初始下渗能力f0、稳定下渗率fc和系数K。这些参数可以由实测资料进行率定,然后就可以用于产流计算。
对于菲利普公式,则有
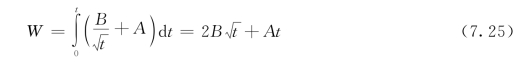
与式(7.22)联立,消去t,得
![]()
式中 A、B——模型的两个待定系数。
上面所介绍的超渗产流计算模型并没有考虑产流面积在流域上的变化,因为计算时采用的是流域的下渗能力曲线。如果考虑产流面积在流域上的变化,计算还要复杂得多,在下渗公式中,还要增加反映下渗能力在流域面积上的分配与变化的参数。
