三、物体的三视图
如图2-7所示,将两个物体向投影面作正投影,所得到的投影完全相同。如果单纯由这个投影图来想象物体的话,既可想象为物体Ⅰ,也可想象为物体Ⅱ,还可以想象为其他物体。这说明什么呢?说明仅有物体的一个投影不能确定物体的形状。这是因为物体有长、宽、高3个方向的尺寸,而一个投影仅反映两个向度,对于上图投影,就只反映长和宽,而不反映物体的高度。由此可见,仅凭物体的一个投影不能确切、完整地表达物体的形状。而在工程设计时,使用的投影图必须能够确切地表达物体的形状,为此,必须采用增加投影面的数量得到一组投影图,来完全确定物体的形状。
确定物体的空间形状,一般需要3个投影,因此用3个投影面,为方便使用,采用3个互相垂直的投影面,如图2-8所示。
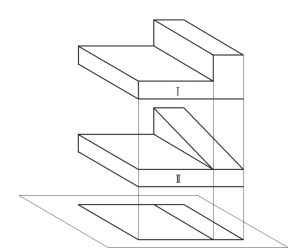
图2-7 物体的三视图
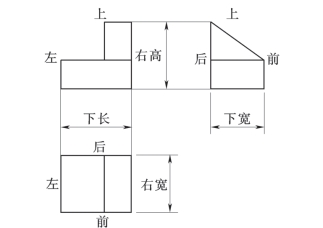
图2-8 三面投影及对应关系
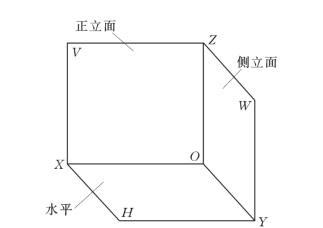
图2-9 三面投影体系
(一)三面投影体系
如图2-9所示,3个互相垂直的投影面,称为三面投影体系,其中:
正立投影面,简称正立面,用V标记;
侧立投影面,简称侧立面,用W标记;
水平投影面,简称水平面,用H标记。
三投影面之间两两的交线,称为投影轴,分别用OX、OY、OZ表示,3根轴的交点O称为原点。
OX轴反映物体的长度,OY轴反映宽度,OZ轴反映高度。
(二)三视图的形成
现将物体放在三面投影体系中,并尽可能使物体的各主要表面平行或垂直与其中的一个投影面,保持物体不动,将物体分别向3个投影面作投影,就得到物体的三视图。注意:三视图是以正投影法为依据的,但具体绘制时,是用人的视线代替投影线的,将物体向三个投影面作投影,即从3个方向去观看。从前向后看,即得V面上的投影,称为正视图;从左向右看,即得在W面上的投影,称为侧视图或左视图;从上向下看,即得在H面上的投影,称为俯视图,如图2-10所示。
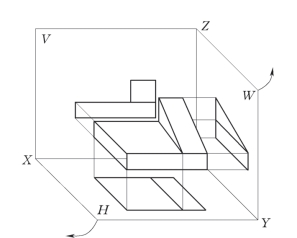
图2-10 物体在三面投影体系中的投影
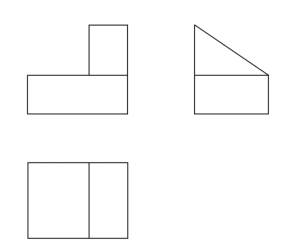
图2-11 展开后的三示图
为方便绘图,使三视图位于同一平面内,需将3个互相垂直的投影面摊平。方法是:V面不动,将H面绕OX轴向下旋转90°,W面绕OZ轴向右旋转90°。
如图2-11所示,由于投影面的边框及投影轴与表示物体的形状无关,所以不必画出。
虽然用这种方法绘制的工程图样直观性差,但作图方便且便于度量,因此它是工程中应用最广的一种图示方法,也是本课程的研究重点。
(三)三视图的投影特征
由三视图可以看出,俯视图反映物体的长和宽,正视图反映它的长和高,左视图反映它的宽和高。因此,物体的三视图之间具有如下的对应关系:
(1)正视图与俯视图的长度相等,即“长对正”;
(2)正视图与左视图的高度相等,即“高平齐”;
(3)俯视图与左视图的宽度相等,即“宽相等”。
在三视图中,无论是物体的总长、总宽、总高,还是局部的长、宽、高(如上面的棱柱)都必须符合“长对正、高平齐、宽相等”的对应关系。这是绘制和阅读三视图必须遵循的对应关系。
物体的三视图与6个方向的关系:
当物体与投影面的相对位置确定之后,就有上下、左右和前后6个确定的方向,由图可看出:
正视图反映物体的左右、上下关系;
俯视图反映物体的左右、前后关系;
左视图反映物体的上下、前后关系。
注意前后位置关系,这是同学们容易出错的地方。在俯视图和左视图中,远离正视图的一边是物体的前面,靠近正视图的一边是物体的后边。
无论何种形状的物体,总是由基本的几何元素点、线、面,依据一定的几何关系组合而成的。为了提高对物体视图的分析和表达能力,我们从构成物体表面的最基本要素点、直线、平面来研究。
