1.4.1 单雨滴碰撞行为模拟
单个雨滴和土壤表面碰撞行为可分为雨滴渗透、雨滴变形及雨滴碰撞前表面速度分布、颗粒加速及起跳等(Furbish, et al., 2007)。
单个雨滴和土壤接触后会向具有一定孔隙度的土表渗透。这里设雨滴的直径为Dr,密度为ρr,雨滴碰撞速度为Vim, 则在液固界面的碰撞压力P可满足式(1-1):
单个雨滴渗入土壤孔隙中(土壤粒径为Ds)的深度δ与碰撞界面雨滴的压力和土壤孔隙之间空气压力差值有关(设孔隙度为φ),假定入渗过程中空气被完全排出,则根据达西定律可有式(1-2):
根据渗透性和孔隙度的关系有式(1-3):其中A为常数。
考虑碰撞时间t正比于
,则对式(1-2)积分后可得无量纲渗透距离式(1-4):
根据雨滴深度可计算雨滴渗透剩余体积(excess volume)σ(总体积减去渗透体积),见式(1-5):
雨滴和土壤表面碰撞后发生了复杂变形,此过程伴随着雨滴动量传递到碰撞点周围的土壤颗粒。为了表征动量传递过程,这里给出雨滴表面各处速度的分布函数式(1-6):其中斜面倾角为α,θ为雨滴径向速度Vims的方位角,径向速度是指雨滴碰撞速度在碰撞界面上以雨滴中心为坐标原点,任意方位角对应的速度,其大小满足Vims~1/3Vimcosα,当θ=0时径向速度为下坡向速度。无量纲径向速度
, 其中γ为雨滴碰撞速度在径向和法向(垂直于碰撞平面)投影速度的比值,据此,V(θ)概率密度函数可表示为式(1-6):当α=0时,雨滴动量的径向分布具有均匀分布特征;当碰撞界面倾斜时雨滴下坡向的动量随着坡度的增大而增大。
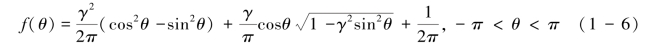
在平坦的溅蚀表面,根据动量定理,单雨滴溅射的土壤颗粒的动量满足msΔVs=FΔt,F为雨滴变形过程对土壤颗粒的作用力,Δt为作用时间。考虑到流体对颗粒作用力与流体碰撞过程中压力成正比,运用量纲分析有式(1-7)、式(1-8)和式(1-9):其中ζ为无量纲数,反映了雨滴动量传递给溅射颗粒的份额。单雨滴与单粒径沙粒的碰撞数据显示该参数的数量级为0.001 (Furbish, et al., 2007)。
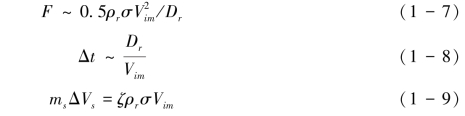
假定ΔVs的数量级受水平面上平均实测的溅射径向距离Ψ∗和时间间隔τ的控制,利用量纲分析则存在式(1-10)的关系:其中实测数据拟合表明ζτ的数量级为0.001 s (Furbish, et al., 2007)。
结合相关溅射距离的数据,假定平面上径向溅射距离L满足式(1-11)的负指数分布函数:其中Ψ0为L的平均值,r0为排除距离,它可以看作是雨滴碰撞足迹的半径,其意味着在雨滴碰撞中心,溅射径向距离的分布特征不符合负指数分布函数。
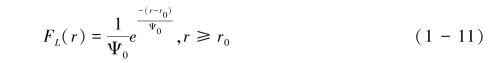
函数式(1-11)反映了在平坦的土壤表面上,溅射距离的概率与θ无关。在坡度为α的斜面上,任意θ的径向溅射距离Ψ(θ)可用式(1-12)表示:
函数式(1-12)是基于这样的假定:①在任意θ情形下所有溅蚀颗粒的动量是与θ方位的雨滴平均动量成正比且与α无关;②在溅蚀质量一定情况下,溅射距离正比于雨滴的动量如式(1-10),这样就可以用无量纲径向速度来修正式(1-11)从而得到式(1-12)。注意式(1-11)的积分结果就是Ψ0。
据函数式(1-6)、式(1-11)和式(1-12)可求得斜面上径向溅射距离L和方位角的联合概率密度函数FLΘ式(1-13):
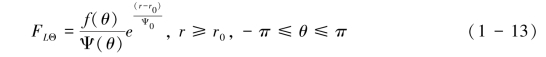
通过极坐标和直角坐标系的转化,式(1-13)可变化为式(1-14),FX(x)表示与斜坡平行的溅射距离X的边缘概率分布,FXY(x,y)为任意dxdy内溅射距离的联合概率。
下坡向平均溅射距离ΨX可表示为式(1-15),该积分可获得数值解。鉴于在计算方面ΨX的困难,这里引入无量纲溅射距离Ψα,它可定义为式(1-16):
根据ΨX的数值结果、Ψα和斜面坡度的正切值tanα近似服从线性关系的事实,则用线性系数ξ、Ψα和Ψ0来表示ΨX为式(1-17):
模拟实验表明(Furbish, et al., 2007),分别在10 mm·h-1降雨强度和3 mm雨滴的情况下,每个雨滴平均溅射72颗中沙沙粒,对应的Ψ0=2 cm,ξ′=1.74。
设单位面积单位时间内雨滴的数量为Nr,每个雨滴能溅射、移动的土壤颗粒数Ns,则下坡向单位宽度的溅蚀输沙率qN可表述为式(1-18):
式(1-18)为溅蚀颗粒数输送通量函数,其还可以转换为质量通量和体积通量函数。
Furbish et al(2007)模式建模思路可归纳为:引入经验参数γ表征雨滴碰撞速度在径向和法向的比值(其近似地与tanα成正比),建立无量纲径向速度的概率分布函数以模拟单个雨滴动量在液固界面的分布概率;基于无量纲径向速度概率分布模式、斜面上溅射距离和方位角联合概率分布模式模拟溅射距离径向分布趋势及平均溅射距离;根据平均溅射距离、降雨强度和单雨滴动量定义溅蚀输送通量。