3.3.1 风洞观测的粗糙床面风廓线特征
为了研究粗糙床面的空气动力学粗糙度及其对跃移起动的影响,这里设计了38组粗糙床面来观测其风廓线特征、空气动力学粗糙度和跃移起动过程。具体的几何参数见表3-2和表3-3。所有粗糙床面的铺设面积为1 m2。粗糙元密度、方向比率、高度与行间距比等参数的定义分别如下:
表3-2 密实粗糙元模型结构参数(梅凡民等,2010)
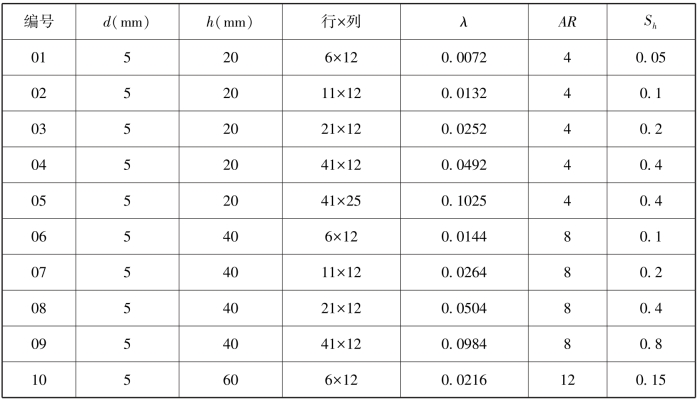
续表
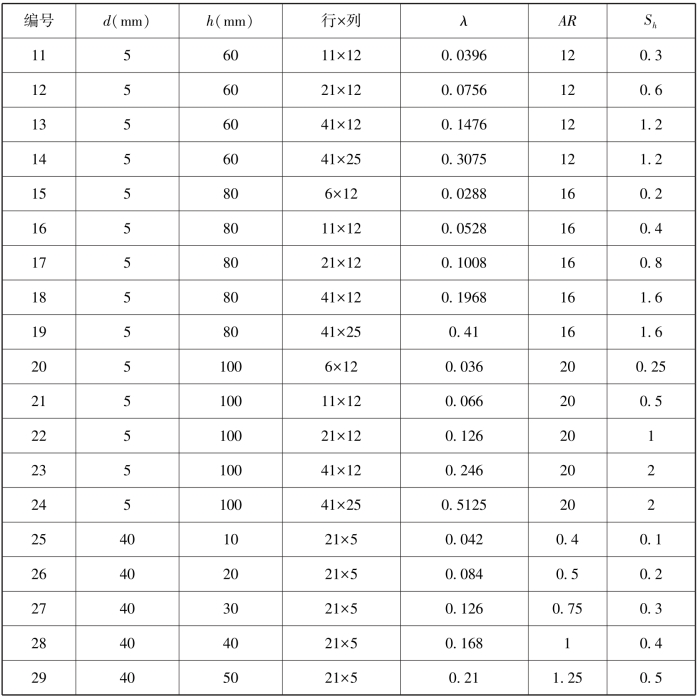
表3-3 孔隙粗糙元模型结构参数(梅凡民等,2010)
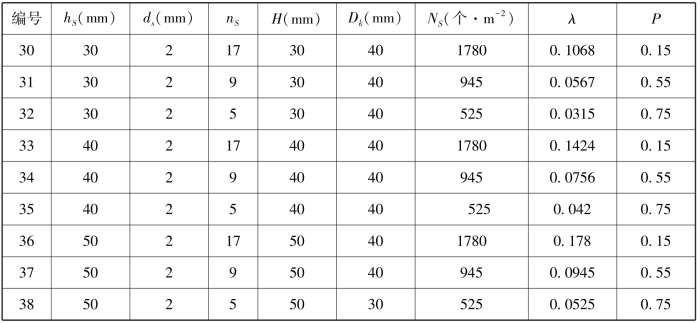
粗糙元密度λ或称侧影盖度指直立植被的总迎风面积与覆盖地面面积之比:

其中,λ为密度,n、h、d分别为植被粗糙元的个数,高度和直径;S为覆盖地面面积。
方向比率AR定义为圆柱形粗糙元的高度与直径比:
![]()
高度与间距比Sh定义为式(3-27),其中,Sp为两个相邻粗糙元之间的距离:

粗糙元孔隙度定义为单个植株孔隙度粗糙元的迎风面积与此粗糙元中所有分散粗糙元总迎风面积的比值,以式(3-28)表示:

其中,H、Dk为孔隙植被高度与直径;ns, hs, ds为分散在孔隙粗糙元中单个粗糙元的个数、高度与直径(见图3-8)。
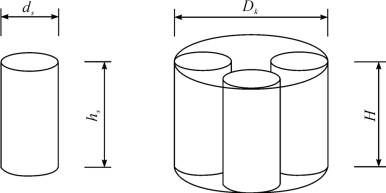
图3-8 粗糙元孔隙度计算示意图(梅凡民等,2010)
为了保证风洞模拟实验结果和野外实际情况的可比性和相似性,这里用相似准则参数雷诺数(Rep)来判定实验模型几何高度选择的合理性。雷诺数(Rep)定义为式(3-29):
![]()
式中,U为风速;L为特征长度;ν为动力黏滞系数(常温常压下ν≈0.15 cm2·s-1)。在我国干旱、半干旱地区,植被的高度约为40~120 cm之间,气象站典型风速500 cm·s-1, 根据式(3-25)计算得雷诺数Rep=1.33×105~4.0×105。本次风洞实验的最大风速为20 m·s-1,植被模型的最大高度10 cm,计算得此种实验条件下的Rep=1.33×105,与野外情况相似。实验使用风洞Rep=105~106,其流态是完全湍流的达到模拟要求。风洞实验段的风速廓线符合对数分布律,其与自然界相似。根据雷诺数限制和风洞边界层厚度,所有模型高度在10~100 mm是合适的。(https://www.daowen.com)
考虑到粗糙元覆盖床面的异质性特点和床面湍流边界层发育状况对风廓线的影响,分别在粗糙床面前段、中段和末段布置测点以了解床面气流特征,另外布置了下风向相邻粗糙元之间及相邻两列之间的风廓线测点,以了解气流的测向差异。分别将设计并制作好的植被模型按编号依次放入环境风洞实验段,模型底面与风洞的底面重合。每种模型在9种自由风速(4、6、8、10、12、14、16、18、20 m·s-1)下测定风速廓线。风速廓线仪由基本上按对数律布置于不同高度上(3.0、6.0、10.0、15.0、30.0、60.0、120、200、350、500 mm)的10个精细毕托管组成,使用前经标准毕托管标定。风洞中心线风速U,即来流风速用置于实验段入口处轴线位置的毕托管测定。所有毕托管都通过微压差传感器与计算机相连,实验时气温和大气压用计算机键盘键入风压测量系统程序中,实现风速实时自动采集(见图3-9)。本实验风速采集频率为2 s,采集时长60 s,以获得各个高度上的平均风速。
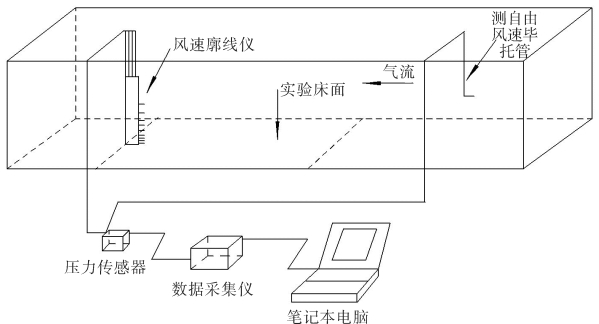
图3-9 环境风洞实验段及实验布置示意图(梅凡民等,2010)
粗糙床面的空气动力学粗糙度根据风速梯度数据来计算:

其中,Z0为植被覆盖地表的空气动力学粗糙度;D为零平面位移高度,其相当于将粗糙元覆盖条件下的零风速高度向上移动的位移量(D),表征了湍流平均动量损失的高度(Jackson,1981)。零平面位移高度也反映了地表对气流的反馈作用,与下垫面特征存在紧密地联系,粗矮和稀疏植被的零平面位移高度较小,甚至接近零, 但随着植被高度和密度增加而增加(刘小平, 2002)。有研究者指出,D值随着地表植被覆盖状况0.02~0.07 m之间变化(Gilles, et al., 2006)。刘小平(2002)计算了大量的风洞实验数据后发现,即使高大粗糙元覆盖床面时,各种床面的Z0和D处于同一数量级。因此,认为D、Z0其中一个参数就能反映地表对气流的反馈作用。由于Z0具有明确的物理意义,所以,在本文中不考虑D的影响,让D=0将使问题得到简化,则式(3-30)得以简化为式(3-31),就可利用多个高度风速值通过最小二乘法计算Z0。
用最小二乘法拟合风速廓线计算Z0已得到很多研究者的认同。风速廓线拟合方程为:
![]()
式中,UZ为高度Z处的风速;a,b为回归系数,则Z0和U∗分别表示为式(3-32)和式(3-33):

其中,К为卡曼常数,取0.4。
拟合结果R2>0.97控制,计算精度。
图3-10和图3-11是测定的部分粗糙元覆盖的床面在9种自由风速(4 m·s-1、6 m·s-1、8 m·s-1、 10 m·s-1、 12 m·s-1、 14 m·s-1、 16 m·s-1、 18 m·s-1、 20 m·s-1)下的风速廓线。从图3-10可以看到在粗糙元高度、直径相同情况下,粗糙元密度对风廓线影响是显著的,密度在0.1以下整个高度风廓线服从对数律,密度大于0.1,植被高度以下风速廓线偏离对数规律,而且这个趋势会随着粗糙元高度和直径增加表现得更加明显。另外在粗糙元密度和直径较小的情况下,风速廓线基本遵循对数规律;粗糙元密度增大时,粗糙元高度以下气流速度会急剧减小。粗糙元直径较大时,在植被后面形成大范围尾流区,从而造成粗糙元高度以下风速趋向为零。
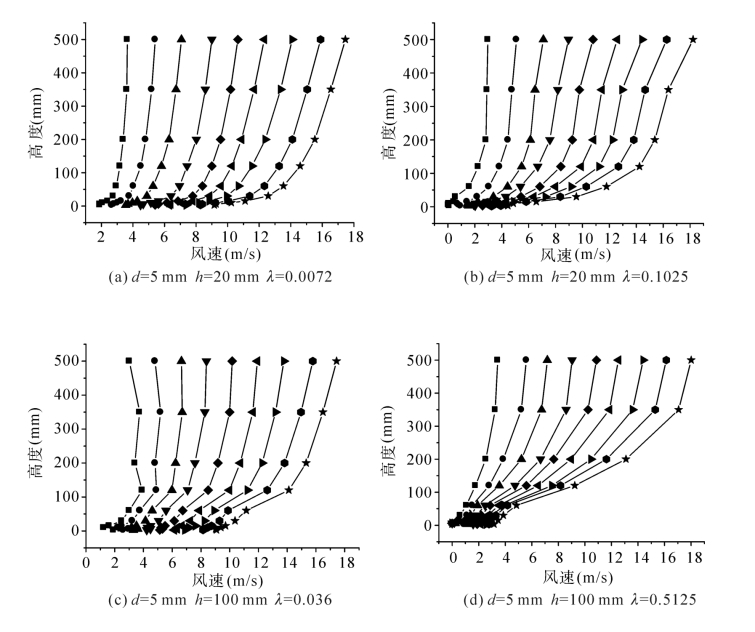
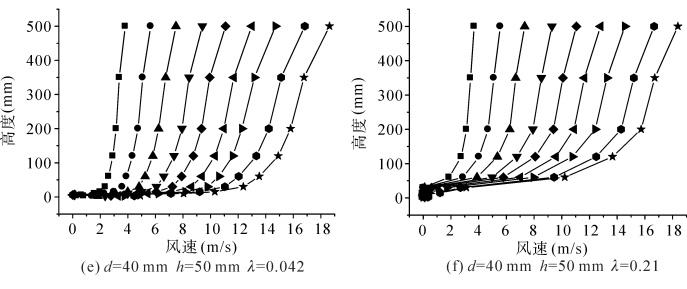
图3-10 密实粗糙元覆盖床面的风速廓线(梅凡民等,2010)
粗糙元孔隙率对风速廓线的影响是显著的,当孔隙度为0.75时(图3-11),粗糙元高度以下风速梯度很小,这主要是由于湍流涡经过大孔隙过滤和分散而导致风速梯度减小;反之当孔隙度为0.15时(图3-11),粗糙元高度以下风速急剧减小,并且与粗糙元以上高度风速形成较大的梯度。
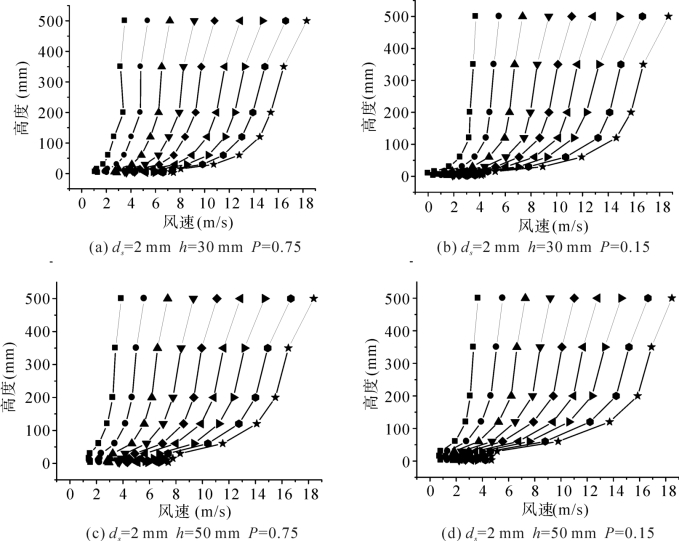
图3-11 孔隙度粗糙元覆盖床面的风速廓线
前人认为植被覆盖床面的气流结构可以分为2部分,植被高度以下为粗糙亚层,以上为惯性亚层(Raupach, et al., 1980)。粗糙亚层气流受植被尾涡的影响较为强烈,植被密度较小时,此层风速梯度随植被特征变化呈明显的随机特征,而当植被密度较大时,此层几乎无气流通过,形成植被顶部掠流;在惯性亚层,气流主要受制于整个植被层,风廓线服从对数律,并受植被特征的影响。
考虑到粗糙床面风廓线具有多个转折段的特征(见图3-10和图3-11),这里给出不同的分析和拟合方法,见3.2.2内容。
