4.4.3　粒-床碰撞模拟计算原理、方法的比较与分析

4.4.3　粒-床碰撞模拟计算原理、方法的比较与分析

粒-床碰撞的计算模式主要包括硬球模式、软球模式以及对硬球模式参数化的解析模式(Lämmel, et al., 2017; Comola ＆amp; Lehning, 2017)等。这里分别介绍硬球模式和软球模式。

4.4.3.1 硬球模型原理及初步计算结果分析

根据线动量和角动量定理,两球碰撞的动量方程组可表示为式(4-56)~式(4-63):

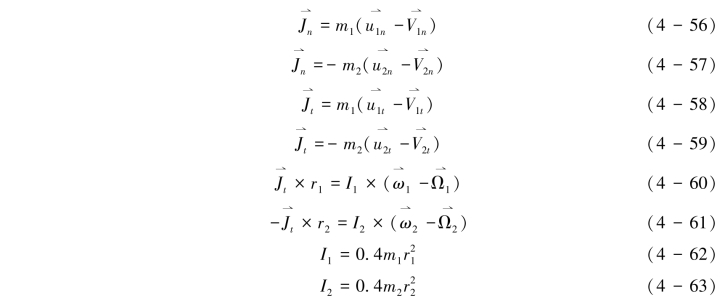
, 是法向和切向的动量, ,分别是颗粒1和颗粒2碰撞前和碰撞后的线速度和角速度, m1, m2, r1, r2, I1, I2 分别是颗粒1和颗粒2的质量、半径和转动惯量。

显然,上述方程组是不封闭的。为了让上述方程组封闭,前人通过引入不同的物理假定和经验参数来封闭方程组,便形成了硬球模式的几个参数化的方案(见表4-8)。

表4-8　硬球模型的参数化方案(kn,kt,μ 分别为法向和切向恢复系数及滑动摩擦系数)

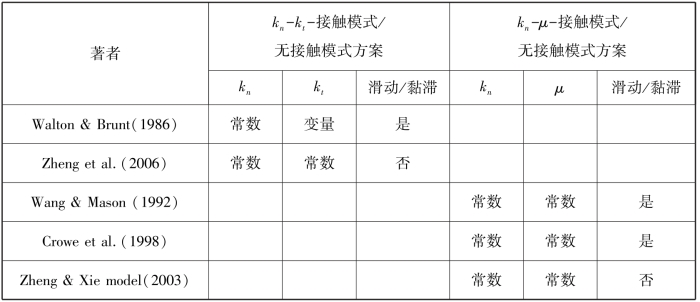
这里kn,kt,分别定义式(4-64)~式(4-70):

关于切向恢复系数kt的设置,前人有2种处理方式,一种是设置为常数(Zheng et al., 2006),一种是如式(4-70)即根据滑动和黏滞两种情形来处理(Walton ＆amp; Brunt,1986)。

表4-8中接触模式是指颗粒1和颗粒2碰撞结束前是否存在滑动的情形,若存在滑动可以摩擦定律来联系法向和切向冲量,如黏滞可定义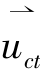=0从而实现动量方程组的求解(Croweetal.,1998)。如果单纯引进摩擦系数而不区分接触关系时,会出现碰撞后动能增加的错误结果,这被称为Kane悖论(Wang ＆amp; Mason, 1992)。

确定接触方式可利用3种方案:①利用式(4-70)通过计算接触角来确定接触方式(Walton ＆amp; Brunt,1986);②通过数学推导的代数式确定滑动与黏滞情形,即式(4-71)和式(4-73)表示滑动的切向冲量而式(4-72)和式(4-74)表示黏滞时的切向冲量。Wang＆amp; Mason (1992)采用Routh's 图法而Crowe et al.(1998)采用数学推导来区分颗粒碰撞的接触关系。

为了理解上不同的参数化方案对计算结果的影响,著者设计了不同的碰撞情景,颗粒1的碰撞前速度在1~10 m·s-1之间变化,颗粒2的碰撞前速度0.5~2 m·s-1之间变化,接触角在0~π之间变化,颗粒粒径均为100 μm,然后用上述模式分别计算碰撞后颗粒速度。在计算结果中去除假碰撞的情境用于数据分析。

图4-11表明Walton ＆amp; Braun模型(1986)和Wang ＆amp; Mason 模型(1992)预测的碰撞后线速度相近(约有90%预测结果的相对误差率在±0.2范围内),而角速度的相对误差率较大(约70%预测结果的相对误差率超过±0.2)。Zheng et al.(2006) 模式预测的角速度误差更大,是因为该模式没有考虑碰撞沙粒之间的接触关系所致。其他版本的解析模式还存在违反动能守恒的现象。鉴于这些解析模式在预测角速度均存在明显的误差,未来的研究应特别关注沙粒三维旋转的观测,期望通过观测数据来修正目前解析模式的误差。

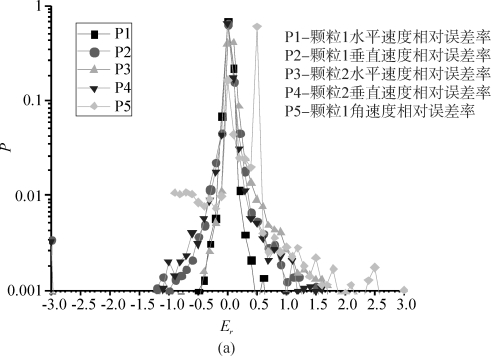
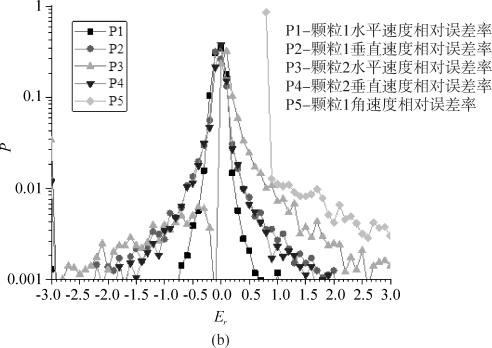
图4-11　(a)Walton ＆amp; Braun模型(1986)对Wang ＆amp; Mason模型(1992)相对误差率的概率分布,(b)Zheng et al.(2006)模型相对于Wang ＆amp; Mason 模型(1992)相对误差率的概率分布

需要说明的是,硬球模型仅适合预测两颗粒碰撞问题,其具有计算简洁的优点,但不适合模拟多颗粒的粒-床碰撞过程。前人利用该类模式模拟粒-床碰撞时,做了一些巧妙的处理。有些研究者是把沙粒碰撞看作是稀相,让沙粒随机组合地两两碰撞完后再次和其他颗粒随机组合碰撞,此算法被称为随机行走(Sun, et al., 2001; Crassous ＆amp; Beladjine,2007; Xiao, et al., 2017)。有些研究者把多颗粒的粒-床碰撞简化为三颗粒碰撞情景以模拟沙粒起跳速度的分布(Zheng ＆amp; Xie, 2003; Zheng, et al., 2006)。上述的处理虽然可以获得起跳速度的概率分布模式,但不易准确地反映粒-床碰撞过程的动量传递等微观的机理,也不易预测床面上颗粒的溅射强度的空间差异及床面形态变化。鉴于此,著者提出一个基于动量传递机理的局部解析算法来模拟粒-床碰撞过程,下面介绍该算法的研究思路和原理:

粒-床碰撞的数值算法之所以能够处理多颗粒的碰撞问题,是因为它具有两个功能:一是搜索功能,在每个计算步长内会搜索与所研究颗粒相撞的颗粒,以确保完备地追踪到所有的碰撞颗粒。二是矢量合成的思路和方法,先分别计算其他颗粒对所研究颗粒的法向和切向作用力,然后用矢量合成方法计算所研究颗粒所受的合力。

拟发展的算法(后面简称新算法)借鉴了数值算法上述的两个功能后,把矢量合成的思路和方法引入到解析模式,就可以用经典的解析模式来模拟多颗粒的碰撞。

为了把矢量合成的思路和方法用于新算法,需要引进动量传递系数。设入射沙粒i的质量为m(i),以初始速度V0(i)与床面k沙粒相撞,其传递给k沙粒的动量为ei,k(i,k)·m(i)·V0(i), ei,k(i,k)称为i对k的动量传递系数,且满足0＆lt;ei,k(i,k)≤1,床面颗粒动量传递系数的定义与入射颗粒相同。

若动量传递系数和初始碰撞参数已知,就可以用解析模式分别计算所研究沙粒与其他沙粒碰撞后的线速度和动量矩,然后利用矢量合成的方法计算碰撞后所研究沙粒的水平和垂直速度及角速度。

新算法被称为局部解析算法是因为它不能提供描述多颗粒碰撞的解析式,故不是完全意义上的解析算法,但对单次碰撞的两颗粒而言,它们碰撞后的速度是用解析模式计算,故称为局部解析算法。

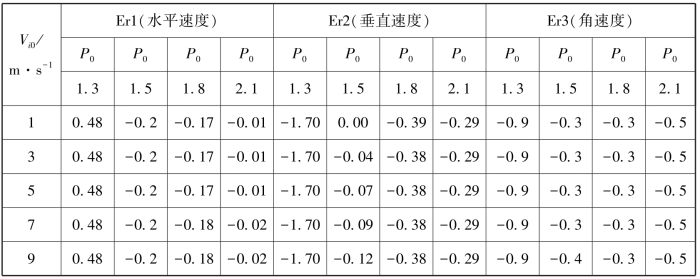
这里以前期研究粒-床碰撞算例来说明。以直径为100 μm的入射沙粒与一个规则排列的6×6等直径的二维圆饼床面的碰撞算例来说明(见图4-12~图4-15),沙粒分别以1, 3, 5, 7, 9 m·s-1的速度(入射角为-0.2)、分别以1.3, 1.5, 1.8, 2.1弧度的接触角和床面4号沙粒碰撞。令 ei,k(i,k)和ekj(k,j)分别等于1和0.25(考虑到k可能和4个沙粒同时碰撞,i颗粒和1个床面沙粒碰撞)。分别用新算法和数值算法计算碰撞后沙粒的速度,并以数值算法的结果为参比计算新算法的相对误差率。

新算法和数值算法预测的结果有相对一致性,都体现了动量的非均匀传递的趋势,且均符合能量守恒定律(见图4-12~图4.15)。新算法表明3, 4, 5, 8, 9, 10号沙粒的水平速度约为入射速度的10%;数值结果显示6号颗粒的水平速度约为入射速度的40% 而34号或35号沙粒的垂直速度约为入射速度的-40%。新算法计算的反弹颗粒和床面沙粒的动能之和约为入射沙粒动能的44%~67%(见图4-12~图4.15),其和数值算法相似。

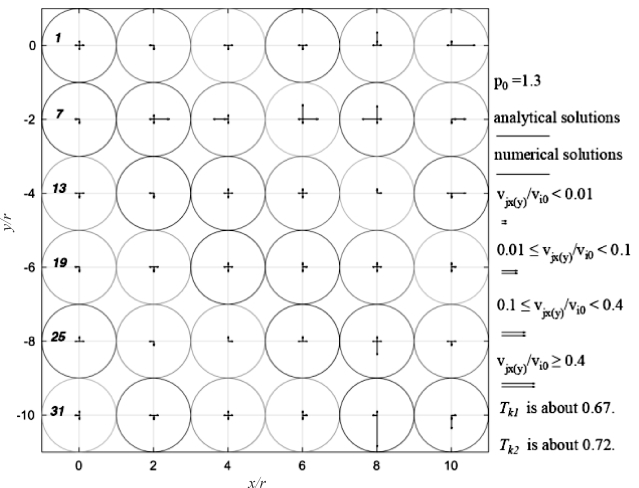
图4-12　模拟的床面沙粒的水平和垂直速度

P0为接触角,r为沙粒半径,Vi0为入射速度,Vjx,Vjy为床面沙粒碰撞后水平和垂直速度;Tk是碰撞后入射和床面沙粒的动能与入射动能的比值,1是来自与新算法,2是来自于数值算法,用Mindlin ＆amp; Deresiewicz (1953)模型计算法向力,Cundall ＆amp; Strack(1979)模型计算切向力。

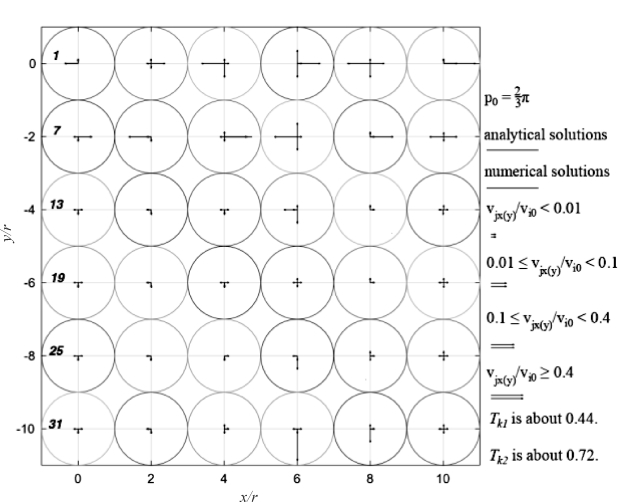
图4-13　模拟的床面沙粒的水平和垂直速度(图例同图4-12)

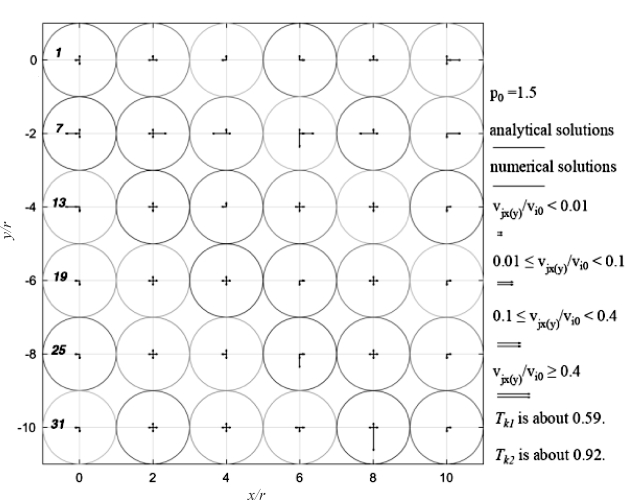
图4-14　模拟的床面沙粒的水平和垂直速度(图例同图4-12)

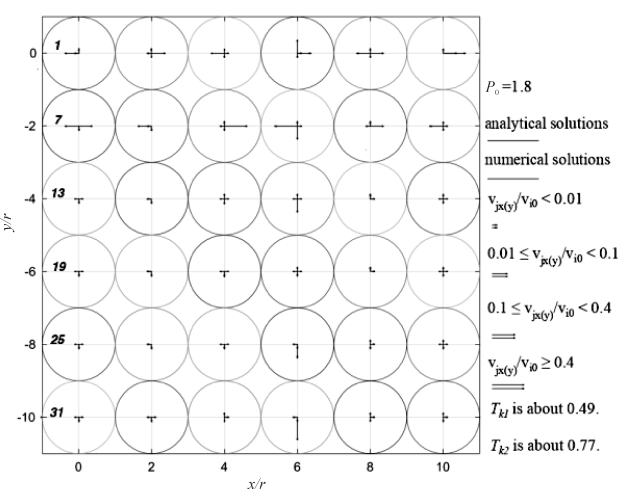
图4-15　模拟的床面沙粒的水平和垂直速度(图例同图4-12)

图4-12~图4-15的4个算例均表明无论是入射碰撞角是锐角还是钝角、入射速度是低速还是高速,新算法和数值算法预测结果在趋势上的一致性,即动量在床面上的传递是非均匀的过程:新算法水平动量集中于3, 4, 5, 8, 9, 10号而数值结果显示水平动量集中于6号颗粒,垂直动量集中于34号或35号沙粒,这取决于入射接触角。

eik(i,k) 和ekj(k,j)被设置成常数是造成新算法和数值算法差异的主要原因。从数值算法来看,当满足e5,6(5,6)＆gt;e5,11(5,11)的条件才可能使5号沙粒把大部分的动量传递给6号沙粒,同时还应满足 e5,6(5,6)＆gt;e6,5(6,5)＆gt;e6,12(6,12),才能使6号沙粒最大程度保有5号沙粒传递的水平动量。同理,其他沙粒间的动量传递系数也应该有类似的变化。唯有如此,新算法预测结果才会与数值算法接近、与实际的粒-床碰撞情形接近。这意味着粒-床碰撞过程中存在着一个未被精细刻画的动量非均匀传递机理。

从入射沙粒的碰撞结果看,新算法和数值算法预测结果具有相对的一致性(见表4-9):在入射沙粒接触角为钝角的情况下,新算法预测的入射沙粒碰撞后线速度和角速度的相对误差率分别不超过40%和54%;当入射接触角为锐角时,入射沙粒的垂直速度和角速度的相对误差率超过1倍,这是因为入射沙粒和4号沙粒碰撞后会继续向下运动再与5号颗粒相撞后才反弹离开床面,这是新算法初期版本缺少再碰撞搜索的功能所致。增加再碰撞搜索功能即可解决此问题。

表4-9　新算法计算的入射沙粒碰撞后水平速度、垂直速度和角速度的相对误差率(P0-接触角,单位为弧度,Vi0入射速度,Er1, Er2, Er3分别为水平、垂直速度和角速度的相对误差率)

4.4.3.2 软球模型原理及计算结果分析

不考虑颗粒之间黏滞力的情况下,Mindlin ＆amp; Deresiewicz (1953)模型的法向力的计算包括以下的参数和方程:

首先引入法向叠加量ε的式(4-75):

这里R1和R2为两碰撞颗粒的直径,r1和r2是两颗粒球心的位置矢量。

有效弹性模量E∗可表示为式(4-76):

这里E1和E2分别为颗粒1和颗粒2的弹性模型,σ1和σ2分别为颗粒1和颗粒2的泊松比。

有效颗粒半径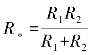,则颗粒间的法向力N为式(4-77):

Mindlin ＆amp; Deresiewicz(1953)模型切向力的计算考虑了切向力加载、卸载及卸载后重新加载的过程,计算十分复杂,后人对其进行了简化(孙其成和王光谦,2009),计算过程如下:

由式(4-77)可计算每一步法向叠加量的增量ΔN可表示为式(4-78):

设两颗粒在接触面上的切向位移为δ,切向力为T,则Δδ对应的ΔT可表示为式(4-79):

式(4-79)中的,p可分别取0, 1, 2,对应切向力加载、卸载和卸载后重新加载,f为动摩擦系数,G∗为有效剪切模量,可用式(4-80)表示:

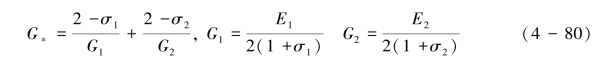
若|ΔT|＆lt;fΔN, 则Θ=1;若,则有式(4-81):

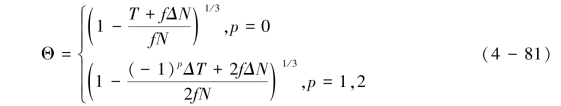
当两颗粒碰撞被看作是弹簧振子系统时(Cundall ＆amp; Strack,1979),法向力和切向力可分别用以下公式来计算,此计算模式可称为弹簧振子模型:

法向力可表述为式(4-82):这里cns和cnd分别被称为法向弹性系数和阻尼系数。切向力可表述为式(4-83):这里cts和ctd分别被称为切向弹性系数和阻尼系数。如果, 则, 否则切向力计算仍采用式(4-83)。

对比接触力模型和弹簧振子模型可发现,后者计算过程相对简洁,很多研究者采用此模式来预测粒-床碰撞后沙粒起跳速度分布和溅射颗粒数目。

为了理解粒-床碰撞过程中入射颗粒的动量传递过程,这里对均一粒径情况下,规则和错位排列情况下动量传递过程进行了计算,颗粒排列情况定义见图4-16。

图4-16　沙粒规则排列示意(左)和错位排列(右)的示意图(颗粒编号与图4-15相同)(魏明孝,2020)

这里设置入射速度Vi0=4 m/s,接触角P0=1.9,入射角C0=-0.2,步长t=5×10-5s,床面颗粒初速度为零。在规则排列下,第一层被撞颗粒的水平速度的变化见图4-17。

床面沙粒的水平速度的变化具有边界效应(见图4-17),入射颗粒的动量先传递给被撞的颗粒3,然后随着碰撞过程中动量的传递,绝大部分的水平动量传递给第一层右边界处的颗粒。

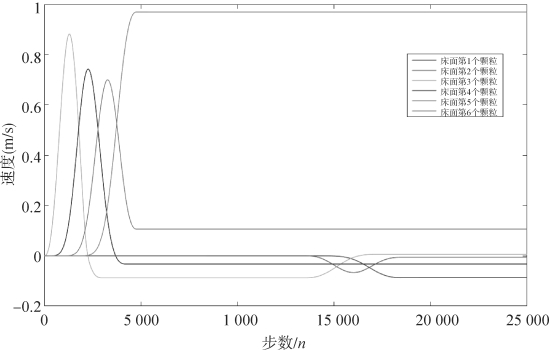
图4-17　规则排列下床面第一层颗粒的水平速度随时间的变化(魏明孝,2020)

床面沙粒的垂直速度的变化仍具有边界效应(见图4-18),入射颗粒的垂直动量先传递给颗粒3,然后依次传递给下边界处的第33颗粒。

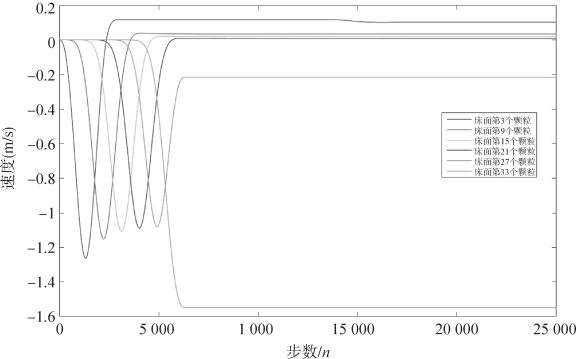
图4-18　规则排列时第3,9,15,21,27,33颗粒垂直速度随时间的变化趋势(魏明孝,2020)

床面颗粒群速度的此涨彼落的特征显示了颗粒间通量传递过程,但目前还没有统一的物理量来表示这一过程,未来的研究需要借助物理学视角给此现象以宏观的概括和总结。

错位排列虽会影响入射颗粒的水平和垂直动量的传递过程,但边界效应和此涨彼落的格局是不变的,有兴趣的读者可参阅文献(魏明孝,2020)。

4.4.3.3 软球模型和局部解析算法的数值算法框架

为了便于读者进行代码编写和理解局部解析算法,这里给出算法框架和相关说明。

数值算法中床面构造的算法和方法(见图4-19):用冷却算法(Powell, 1980)构造沙质床面、沙砾质戈壁床面。鉴于沙砾质戈壁床面和稀疏植被覆盖床面堆积结构和成因较为复杂,因而用冷却算法构造的床面堆积结构时需要根据野外调查信息予以调整。

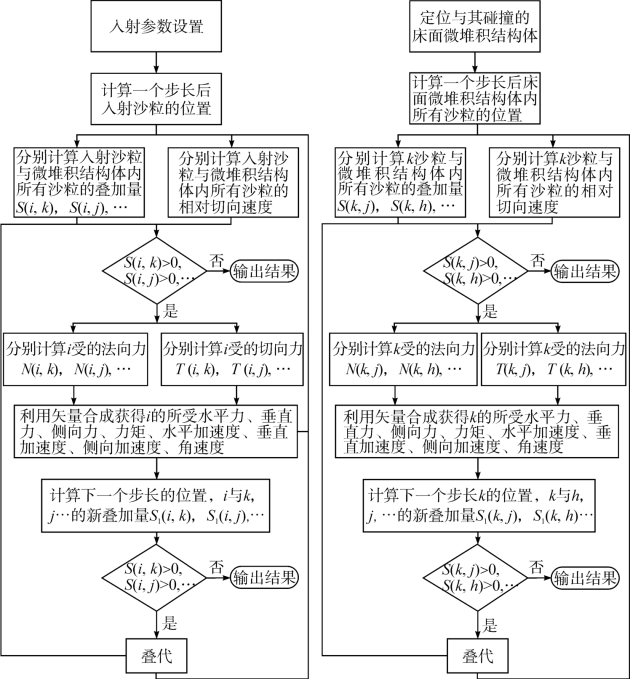
图4-19　软球模型的算法框架

关于床面微堆积结构体参数及分布的定义:数值算法构造的各类风蚀床面不同位置的微堆积结构体参数(S号沙粒位置(最初与入射沙粒相撞的沙粒)、相对于S号沙粒的法向距离、粒径及粒径分布参数、接触角及接触角分布、接触颗粒数)会有差异。微堆积结构体参数的差异及其在床面上的分布是粒-床碰撞数值算法和新算法的试验方案设计的依据。

粒-床碰撞计算的交互性试验方案的设计:粒-床碰撞结果取决于入射参数与微堆积体参数的相互作用,其计算方案应体现多因素交互作用的特点,故采用交互试验方案来设计微堆积体参数以体现多因素交互作用的特点。

构建数值算法:采用接触力模型模拟法向力,采用软球模型模拟切向力,以入射沙粒为研究对象搜索与其碰撞的每一个沙粒,根据每个步长内法向叠加量和切向位移确定法向力和切向力,计算其所受合力、加速度、下1个步长的位置,循环计算直到和所有沙粒分离;床面沙粒算法与其相同,通过循环遍历可模拟完整的粒-床碰撞事件,其算法框架见图4-19。其中法向叠加量等于两沙粒半径之和减去两沙粒的质心距离。切向力计算是需要把摩擦力大小与软球模型预测的切向力比较,若后者大于前者,采用前者,否则采用后者数值。

构建沙粒动量传递系数的多元统计模式:该参数受入射参数、微堆积结构体参数的综合影响,来自交互性数值试验的数据通过多元统计回归方法逐步剔除次要参数,建立包含重要参数的多元统计回归模式。

局部解析算法框架见图4-20,具体包括以下几个方面:

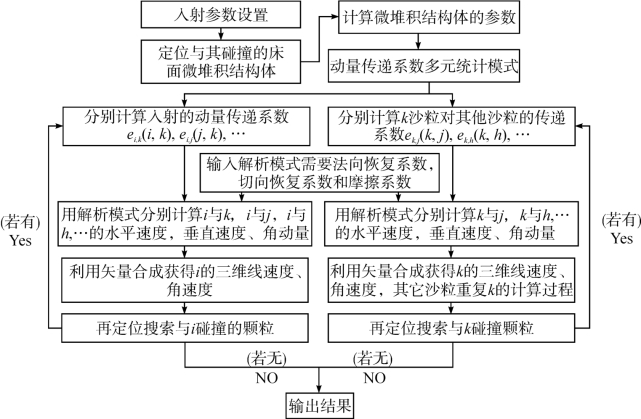
图4-20　局部解析算法的框架

采用数值试验构造的床面、所设计的交互性试验方案。

输入入射参数,搜索定位碰撞的床面微堆积结构体。

输入微堆积结构体的参数计算入射沙粒的动量传递系数、用解析模式计算入射沙粒的碰撞后速度、再碰撞搜索、计算碰撞后速度并输出。

床面微堆积结构体内沙粒速度的计算与入射颗粒的计算程序相同。

新算法的再搜索功能:入射沙粒和床面微堆积体内同时接触的沙粒碰撞后,在低入射角下还会继续向床面下方向运动和其他颗粒碰撞,故用再搜索功能追踪下次碰撞事件(通过设置时间步长,计算沙粒的新坐标,然后搜索与其碰撞的沙粒),其算法和初次算法一致。床面沙粒之间的碰撞也采用再搜索功能来处理此问题。

新算法局部解析解的获得依据Walton ＆amp; Braun (1986)模型,该模式适合模拟三维碰撞过程,且精度与其他模式接近。