3.1 光滑床面大气边界层时均特征与起动摩阻风速
光滑床面是指无风力不可侵蚀物质覆盖的平坦地表。风力不可侵蚀组分称为粗糙元(roughness elements),如沙面上稀疏的植被、直径> 2000 μm的砾石或土壤团聚体等。在中性层结下,流体边界层包括大气边界层的平均风速廓线是符合对数律(Nieuwstadt,1978; Frangi & Richard, 1999),可表示为式(3-1):

其中,U(z) 为高度z处平均风速,U∗为摩阻速度,它表征了湍流平均剪切应力,Z0为空气动力学粗糙度,是指流速为零的高度,其反映了光滑壁面对流体的阻力效应。
非中性层结下风廓线方程(Nieuwstadt, 1978; Frangi & Richard, 1999)为式(3-2)和式(3-3):
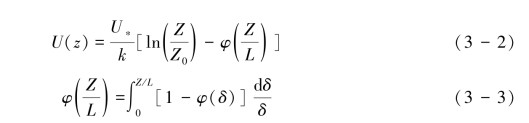
其中U(z), U∗, k,Z0, L分别为风速、摩阻风速、卡门常数、空气动力学粗糙度和莫宁-奥布霍夫长度。莫宁-奥布霍夫长度计算式为式(3-4):
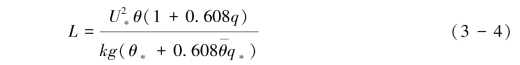
其中θ,θ∗ q, q∗分别为潜热、潜热尺度、湿度及湿度尺度。
里查孙数 (Ri) 是衡量大气稳定度的重要参数,它是根据湍流半经验理论和风温梯度的观测数据而获得的。当Ri>0为稳定层结,Ri=0为中性层结,Ri<0为不稳定层结。在自然条件下,中性层结是非中性层结的一种极限情况,其在每日中维持时间比较短,故取-0.02<Ri<0.02为近中性层结(Nieuwstadt, 1978; Frangi & Richard,1999),Ri>0.02为稳定层结,Ri<-0.02为不稳定层结。
空气动力学粗糙度反映了地表特征对大气湍流的阻抗作用,是描述陆地表面动量、能量和物质交换与输送重要参数之一。在风沙物理学里,该参数是判断跃移起动的重要依据(e.g.Marticorena, et al., 1997)。光滑床面的空气动力学粗糙度为表土微团聚体最大粒径的1/30(Bagnold, 1941; Greeley & Iversen, 1985)。
在流体力学和边界层气象学等学科中,空气动力学粗糙度是仅与床面粗糙程度有关的常量,但近年的研究表明,它是随风速和风向等因素变化的变量(Dong, et al., 2001;梅凡民等, 2006,2012),这意味着用空气动力学粗糙度来预测跃移起动时可能存在不确定性。
从2002年春季毛乌素沙地风蚀实验来看(梅凡民等, 2006),沙地的空气动力学粗糙度随风向的变化而变化(图3-1)。为了排除实验场地周围建筑对风场的影响,这里只计算了风向在-30°~15°范围内空气动力学粗糙度(见图3-2),而在此范围内空气风蚀引起表土粒度和起伏等方面的变化不会导致空气粗糙度在数量级上的变化。虽然可以认为平坦沙地属于相对均一的下垫面,但野外湍流观测的空气动力学粗糙度还是随着风向的变化而呈现明显的变化(见图3-1):北西北风向、西北风向和北风的空气动力学粗糙度在10-6~3.5×10-4m之间变化,而东北风向的空气动力学粗糙度大约10-6~1.5×10-4m之间,总体上略低于其他风向。
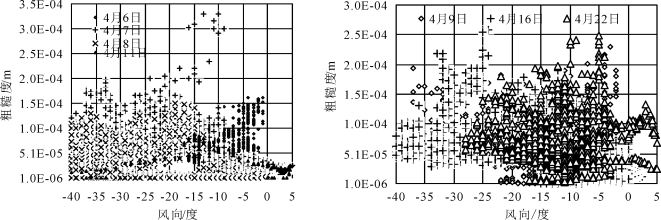
图3-1 风蚀观测日空气动力学粗糙度随风向变化趋势(梅凡民等, 2006)
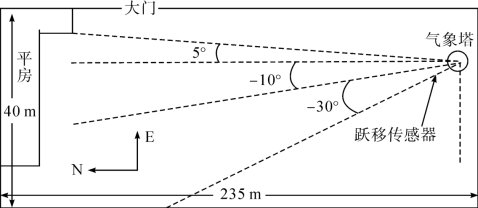
图3-2 毛乌素沙地榆林实验点野外实验地仪器布置示意图(梅凡民等, 2006)
空气动力学粗糙度是十分敏感的参数,影响其变化的因素很多,就目前所知,不外乎3方面的因素:下垫面因素、热力因素和空气动力学因素。空气动力学粗糙度随风向变化的趋势可以理解为地表不均一而导致下垫面的内部差异,如地表微起伏和表土微团聚体粒度分布的差异,事实上,实验地的西北部存在微起伏,表土微团粒粒度分布也具有随机变化的特征,同时,风蚀观测其内出现了鱼鳞状的沙波纹。下垫面的内部差异进而引起空气动力学粗糙度随风向的变化。另外,随着风蚀的进行,地表粗化也能提高空气动力学粗糙度,如对西北风向来说,4月6日~4月22日的7个观测日内,4月16日和22日的粗糙度比6日和7日大(见图3-1),也存在这方面的原因。
除空气动力学粗糙度随风向变化外,在同一风向的条件下,同一个观测日的不同时刻和不同的观测日的粗糙度也存在着明显的变化,其在10-6~3.5×10-4 m之间变化。对于这类变化,需要从热力因素和动力因素方面寻求答案。
尽管由于表土微团粒粒度分布、地表存在微小起伏和鱼鳞状波纹在不同风向上的不均匀分布等方面的原因,使得测定的空气动力学粗糙度在不同风向上存在微小的差异,总体来看,这可能引起起动摩阻风速增大10-1~10-2 m·s-1。从图3-1可以看到在同一风向下,空气动力学粗糙度也存在着明显的变化,其变化也在0.5~2×10-4m范围内,是什么原因导致同一风向下空气动力学粗糙度的变化?
里查孙数 (Ri) 是衡量大气稳定度的重要参数,根据Ri对4月6日至4月23日的8个风蚀观测日的大气稳定度分类,可以看到空气动力学粗糙度随着大气稳定度的不同具有明显的变化(见图3-3),除4月11日和22日稳定层结的历时很短外(基本被归为近中性层结)外,其余观测日的大气稳定度的3种形式都存在,只不过随着春季气温的回升不稳定层结持续的时间更长。除4月9日部分时刻外,稳定层结下空气动力学粗糙度约在10-6~10-5 m之间变化,低于近中性和不稳定层结下的数值;近中性层结状况下,空气动力粗糙度约在10-6~10-4 m之间变化,大部分时刻在10-5 m范围内变化;在不稳定层结下,除4月9日和22日,其他观测日-0.12<Ri<-0.02之间,对应的空气动力学粗糙度约在0.5~3×10-4m之间变化。
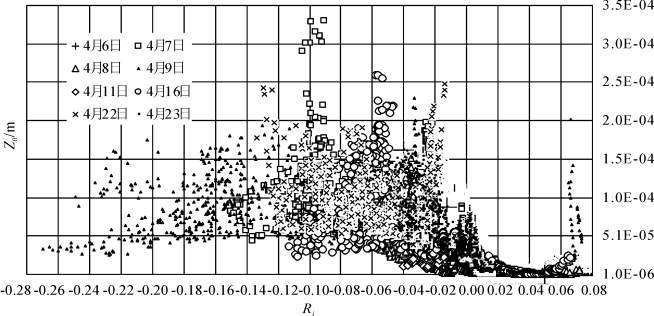
图3-3 风蚀观测日空气动力学粗糙度与里查孙数Ri的变化(梅凡民等, 2006)
上述观测数据表明大气稳定度是影响空气动力学粗糙度的重要因素之一,对此可以做如下解释:在风速相同情况下,不稳定层结与近中性层结相比较,其边界层湍流不但存在机械湍流,而且因为负温度梯度的存在而发育了热力湍流,引起湍流通量增加,相当于强化了地表几何粗糙度引起的机械湍流,其在效果上等效于空气动力学粗糙度的增大(似乎地表变得相对粗糙);与此相反,在相同风速的稳定层结下热力湍流会减弱,几何粗糙度引起的机械湍流强度,则空气动力学粗糙度的减小(似乎地表变得相对光滑)。由此看来非中性层结的空气动力学粗糙度包含了更多的表观成分,它在一定程度上“放大”了或“减弱”了反映地表几何粗糙度的空气动力学信号,而在近中性层结下,边界层机械湍流受到热力湍流的影响小,根据湍流强度测定的空气动力学粗糙度主要反映了下垫面几何粗糙度的影响,其与非中性层结的空气动力学粗糙度的物理意义有所不同。因此在实际应用过程中,根据研究目的选择具有不同物理意义的空气动力学粗糙度是必要的。(https://www.daowen.com)
同一稳定度下,观测的空气动力学粗糙度也存在明显的变化(见图3-3),如4月7日,当Ri=-0.10,风向在-15°左右,空气动力学粗糙度在2~3.5×10-4 m,同样地,其他观测日也存在稳定度和风向相近的情况下,空气动力学粗糙度也存在明显的差异,对此可以从空气动力学因素分析其对空气动力学粗糙度的影响。
空气动力学粗糙度随摩阻风速的变化呈现明显的变化(见图3-4),日出-日落之间摩阻风速相对较大,其在0.15~0.35 m·s-1之间变化,这段时间是一日之中空气动力学粗糙度较大的时候,其变化在10-5~10-4 m之间;日落到日出前,摩阻风速呈现降低趋势,空气动力学粗糙度在10-6~10-5 m之间变化,其间当摩阻风速增大时,空气动力学粗糙度也相应地增大,但这时空气动力学粗糙度的值还是小于相同摩阻风速的白天,这预示着空气动力学粗糙度变化受大气稳定度的影响。
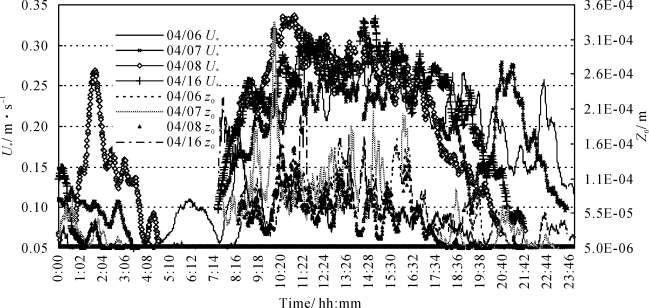
图3-4 风蚀观测日空气动力学粗糙度(Z0)与摩阻风速(U∗)的变化(梅凡民等, 2006)
最近的风洞实验表明沙质地表空气动力学粗糙度不仅受沙粒粒径分布的影响,而且随着摩阻风速的增大而增大(Dong, et al., 2001),上述野外实验结果印证了前人的定性结论。在空气动力学粗糙度随摩阻风速的变化过程中,当地表出现明显的跃移过程时,则属于动床空气动力学粗糙度,或表观粗糙度(apparent roughness length),其反映了跃移对气流的反馈作用。本次实验观测的跃移过程和非跃移过程的平均空气动力学粗糙度的差异(见表3-1和图3-5),证实了跃移输送增大空气动力学粗糙度的结论(e.g.Owen,1964; Gillette, et al., 1998)。
综上所述,根据野外风温廓线法测定的空气动力学粗糙度的变化具有3个方面的物理意义:近中性层结的空气动力学粗糙度较少受主要反映了下垫面的几何粗糙度对湍流的影响,而非中性层结的空气动力学粗糙度不但受到下垫面性质的影响,还反映了热力湍流对机械湍流的增强或削弱作用;风沙流反馈效应也是空气动力学粗糙度增加的重要原因。空气动力学粗糙度不是仅与下垫面性质有关的常数,而是与大气稳定度、摩阻风速和跃移输送等有关的复杂变量。
既然实测的空气动力学粗糙度反映了地表热力因素和动力因素的共同影响,它是随热力因素和动力因素变化的变量,那么由热力因素或动力因素的改变而导致的空气动力学粗糙度的变化,其是否影响起动摩阻风速?这一点对风蚀是十分重要的。表3-1的数据可以回答这个问题。
从表3-1可以看到:不稳定层结下平均空气动力学粗糙度在0.5~1.1×10-4 m之间,近中性层结下平均空气动力学粗糙度在1.2~4.5×10-5 m之间,稳定层结下平均空气动力学粗糙度在3×10-6~2×10-5 m之间;同一个观测日,不稳定层结空气动力学粗糙度高而稳定层结的低 (见图3-5),近中性层结介于二者之间,大气热力因素对空气动力学粗糙度的影响是明显的;3种大气稳定度下跃移过程的平均空气动力学粗糙度高于无跃移过程,与前人关于表观粗糙度的论述相一致,说明风沙运动提高了空气动力学粗糙度,同时可以看到稳定层结下往往风速较小,跃移过程对空气动力学的粗糙度影响较小。
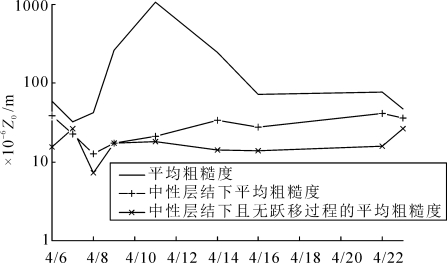
图3-5 风蚀观测期间日平均的空气动力学粗糙度的比较(梅凡民等, 2006)
表3-1 风蚀观测期间日均的不同动力状况和热力状况下的空气动力学粗糙度及观测的平均起动摩阻风速(梅凡民等,2006)
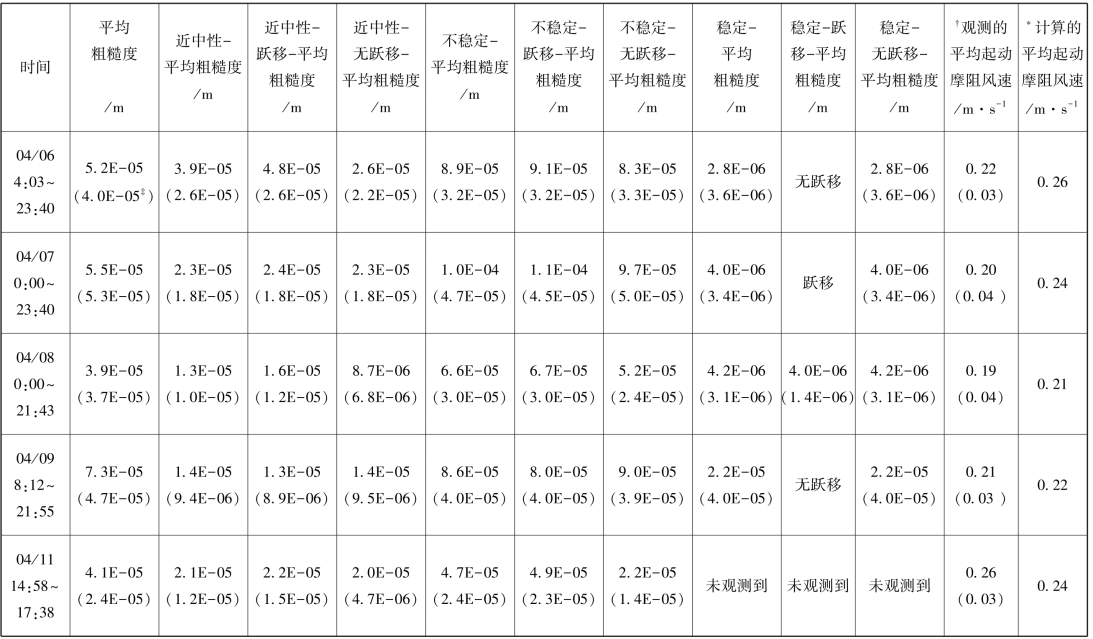
续表
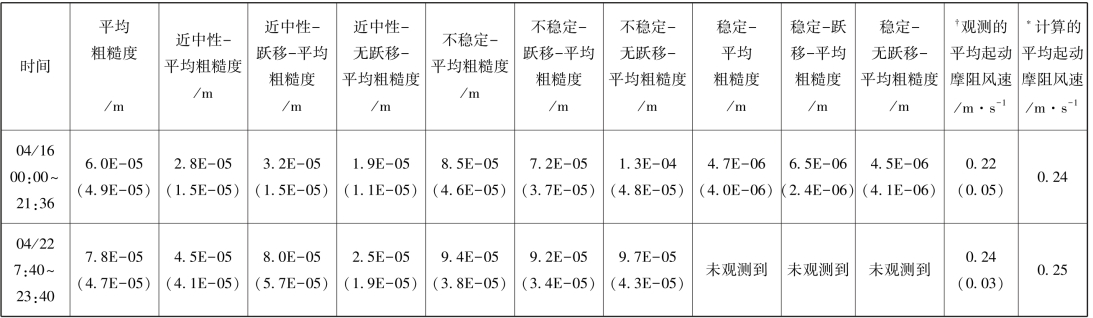
注:‡括号内的数字为标准偏差,†起动摩阻风速是根据跃移传感器记录的每分钟最小撞击次数对应的摩阻风速平均值,起动摩阻风速根据Marticorena&Begamette(1995)计算。
跃移传感器(saltiphone)记录的最小输沙率对应的每日平均起动摩阻风速表明,U∗在0.19~0.26 m·s-1之间变化。近中性层结无跃移过程的平均空气动力学粗糙度计算的起动摩阻风速显示(Marticorena & Begamette,1995),模拟的平均起动摩阻风速在0.22~0.26 m·s-1之间,略高于观测数值。不稳定层结空气动力学粗糙度偏高,如果根据这类粗糙度模拟起动摩阻风速,其值在0.28~0.35 m·s-1之间,明显高于观测值;稳定层结粗糙度偏低,如果按此模拟起动摩阻风速,其值为0.20 m·s-1,明显低于观测值,这说明近中性层结下地表无跃移过程时观测的空气动力学粗糙度对起动摩阻风速是有效的。从物理机制来看,具有一定几何粗糙度的地表吸收了边界层气流切应力传递的部分动量,使得表土可蚀性组分吸收的风动量减少而提高了起动摩阻风速,因而下垫面几何粗糙度产生的空气动力学粗糙度是影响起动摩阻风速的主要因素,而空气稳定度只会增加或减弱湍流强度,不会影响到湍流切应力在下垫面的粗糙元和可蚀性组分之间分配,也就不会影响到起动摩阻风速。跃移过程相当于地表增加了粗糙元(如植被)而提高了空气动力学粗糙度,进一步使跃移过程达到自我限制和平衡,因而跃移过程的空气动力学粗糙度不会影响起动摩阻风速。近中性层结的无跃移过程观测的空气动力学粗糙度较少地受到热力因素和动力因素的影响,主要反映了下垫面几何粗糙度的空气动力学性质,适合作为模拟表土起动摩阻风速的参数。
风速和地表性质保持不变的情况下,和近中性层结比较,在不稳定层结条件下,湍流强度增加,其对应着风蚀强度的增大,反之在稳定层结下,空气动力学粗糙度减小,风蚀强度降低,可作如下的解释:大气稳定度会影响风蚀强度因为它会增加或减弱相同风速条件下的湍流强度。按照Owen的理解,跃移过程是一个自约束过程,跃移输送增大了空气动力学粗糙度,限制了跃移强度继续增大,使跃移过程很快达到平衡。需要明确的是,由大气稳定度引起的空气动力学粗糙度变化与下垫面几何粗糙度引起的空气动力学粗糙度变化的物理意义不同。一般来说,下垫面越粗糙,其起动摩阻风速越大,相同风动力条件下风蚀强度越低。
观测的近中性层结平均空气动力学粗糙度在(1~3)×10-5 m之间变化(见图3-5)。根据实验地表土粒度分布计算的平均空气动力学粗糙度为1.4×10-5 m,二者基本一致,说明了模拟的平坦沙质地表平均空气动力学粗糙度比较可靠。模拟大尺度风蚀和粉尘释放事件时很难考虑大气层结对空气动力学粗糙度的影响,但本实验的结论至少说明大气层结对起动摩阻风速影响不大。
在沙漠地区的沙丘地带,前人测定的局地空气动力学粗糙度在(2~3)×10-3 m之间变化(贾立和王介民, 1999),这已经接近了风蚀起沙的上限,但裸露沙丘正是风沙活动最剧烈的地区。实际上,起伏下垫面(包括沙丘)不再是空气动力学意义上的均一地表,在这些区域利用湍流强度观测的空气动力学粗糙度不再具有局地空气动力学粗糙度的物理意义,而是反映了一定水平观测范围(与湍流观测高度有关)的有效粗糙度(尽管在一些研究中仍把其看作局地粗糙度,这在风蚀研究中是不合适的),因而其数值比平坦沙面高2个数量级,此数值对推测研究区域的风应力强度有意义,但对模拟风蚀强度意义不大。这就提出了在沙丘地带如何通过模拟和观测的方法来获得能够用于风蚀,并反映局部地表空气动力学性质的参数,这可能是风蚀观测和模拟工作中一个有意义的课题。
需要说明的是,在野外实际观测实验中,影响空气动力学粗糙度和起动摩阻风速的因素很多,如表土粒度分布、土壤水分、大气稳定度及跃移输送对气流的反馈等因素,在一次风蚀事件中所测定的起动摩阻是动态的变化如图3-4。因而有学者提出把起动摩阻风速看成随机分布的变量来预测输沙强度(Stout & Zobeck, 1997)。
以上的研究都是把驱动跃移起动的大气边界层看作时均过程,而实际上大气边界层是复杂的湍流。在早期的研究中,湍流被看作是一种完全随机的在时间和空间上发生不规则涨落的流动状态,随机性被认为是湍流的基本特征。后来,人们逐渐注意到湍流运动有别于气体分子运动因其还存在自组织的大尺度的运动。Kline(1967)利用氢气泡技术对近壁区水流运动结构进行了研究,发现近壁区并非层流,而是存在着平静期和剧烈脉动交替出现的湍流结构,在底层会出现低速条带(对应着流向涡的发育),低速条带形成和上抛,引发边界层小流剧烈振荡和强烈脉动,其被称为猝发(Burst)。低速条带破裂,会出现一股强烈的流向加速和指向壁面的运动,这被称为下扫(sweep)。边壁区出现一段平静期,又会触发新条带和湍流结构。这一发现极大地改变了以往对边界层近壁区流动的传统认识。此后, Corino(1969),Kim(1971),Smith(1983)又发现低速条带的抬升在外区形成高剪切层,使低速条带发生振荡,然后低速流体向外区喷射、使条带结构破碎,接着一股来自外区的高速流体冲入内区,使由条带破碎引起的紊乱流动变得比较平稳。近壁区的湍流相干结构相继在射流、尾流、自由剪切流、混合层等湍流边界层中被发现。“相干(拟序)结构”这一概念常用于光、声或电动力学领域,表示产生相互干涉的两个波之间的协调关系。流场中的“相干结构”是指湍流能量急剧释放过程对应的湍流结构。它的起始时间和位置是不确定的,但是一经触发,它就以某种确定的次序发展为特定的运动状态,即在随机流场中存在着可辨识的,有明确准统计周期和外形的流动结构如:上抛、小扫、注入、注出等(Lu & Willmarth, 1973)。
相干结构是湍流研究中的重大发现,它表明湍流并不是完全随机的流动,而是具有可检测的有序运动。相干结构对湍流中动量、能量和质量的输运,对湍流的产生、维持、演化和发展起着重要作用。
相干结构不仅存在于实验室平台模拟的边界层流中,而且也存在于实际大气边界层中(e.g.胡非, 1995; Hunt & Morrison, 2000)。因而,讨论风沙颗粒跃移起动机理时,应考虑湍流结构与跃移起动的关系,具体见3.2 内容。
