4.4.2 基于立体视角风沙颗粒轨迹追踪新方法
前人分别采用风洞实验、模拟碰撞实验、理论模拟和数值模拟等方法研究了粒-床碰撞过程,建立了诸多的入射-反弹-溅射速度的定量关系,发展了形式多样的溅射函数(见表4-7)。这些工作有力地推动了学术界对风沙跃移机理的理解,尽管如此,学术界对很少了解三维粒-床碰撞规律。风洞实验(Zhang, et al., 2007; Yang, et al., 2009; O'Brien& Neuman, 2016; Tanabe, et al., 2017)、理论模拟(Zheng, et al, 2008; Lämmel, et al.,2017)和数值模拟(Oger, et al., 2005, 2008; Yang, et al., 2010; Kang & Zou,2010; 李志强等, 2011; Duan,et al., 2013; Tanabe, et al., 2017)均显示风沙跃移及粒-床碰撞具有显著的三维特征,但计算模拟的三维粒-床碰撞结果还缺乏三维同步观测数据的支持,因而开展三维粒-床碰撞实验显得十分必要,而三维粒-床碰撞研究需要发展基于立体视角新轨迹追踪算法(简称新PTV算法,后同)来解决高浓度风沙流轨迹追踪、入射-反弹-溅射关系的计算机自动识别等问题。
4.4.2.1 基于立体视角的风沙颗粒轨迹拍摄方法
流体力学采用的立体视角拍摄方法(禹明忠, 2002; 鲍晓利, 2013)是研究三维粒-床碰撞的最优策略。立体视角拍摄方法的优势在于:①可同步地记录粒-床碰撞过程中沙粒三维运动的多视角信息,这是基于片光扫描技术(O'Brien & Neuman, 2016, 2017)和离焦成像技术(Pereira & Ghan, 2002; 鲍晓利, 2013)等间接研究沙粒或流体示踪粒子三维运动的二维拍摄方法所不具有的优势;②有助于提高二维影像轨迹追踪的配准率。二维影像中近球形石英砂颗粒的轨迹配准率仅有18%~35% 而沙漠沙的轨迹配准率仅有9%(O'Brien & Neuman, 2016, 2017)。造成轨迹配准率低的首要原因是因为具有侧向速度的沙粒会不断地进入/逸出二维影像从而导致它们不能匹配而被删除或被错误地匹配,若有立体影像的信息则相关算法就可以有效地追踪在二维图像中被删除的颗粒从而提高轨迹的配准率。③有助于保证沙粒轨迹数据的代表性及统计意义。较低轨迹配准率的传统算法所取得的结果仅反映了那些形状规则或侧向运动速度较小沙粒群的轨迹特征而很难反映大量的具有显著侧向运动或形状不规则的沙粒群的轨迹特征(O'Brien & Neuman,2016, 2017; 彭青宇, 2020),这意味着二维影像沙粒群轨迹统计结果具有一定的局限性,而立体视角却能很大程度地克服此局限性。总之,立体拍摄不但可同步地记录粒-床碰撞过程中沙粒的三维运动,且有助于提高沙粒轨迹追踪的配准率,从而保证提取数据的代表性及统计意义。基于经济因素和研究效果的权衡,著者推荐三视角的立体拍摄来研究三维的粒-床碰撞过程(见图4-6)。
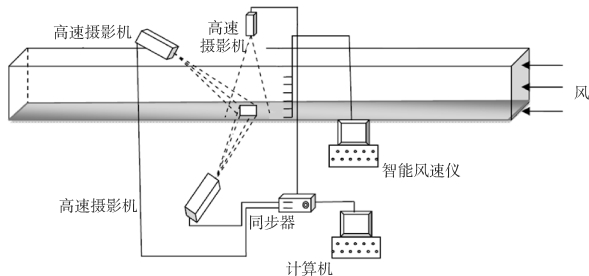
图4-6 风洞实验高速摄影三维拍摄的示意图
立体拍摄的构成:正视拍摄为相机镜头与风向垂直且焦平面与风洞轴流风向平面重合;俯视垂直拍摄是相机镜头与床面垂直,其拍摄焦平面距离床面的高度需要根据具体实验来确定;侧视倾斜拍摄是以相机镜头焦平面与床面以非直角的倾角来拍摄,具体倾角设置需要根据具体的实验场景确定。
拍摄视场的优化方法:以垂直俯拍和侧视斜拍所能捕捉到的侧向运动沙粒轨迹的数量和影像质量来判断。垂直俯拍的焦平面高度以靠近床面为宜,同时考虑床面反光等因素的干扰,具体高度需要根据风洞实验工况如摩阻风速和沙粒浓度来确定。侧视斜拍焦平面和床面夹角以观测的侧向运动沙粒数量和影像清晰度等综合判断后确定。据此建立立体拍摄的优化方案。
拍摄视场的标定方法:拍摄视场的标定采用前人推荐的方法进行(禹明忠, 2002)。在风洞内布置立体正交的金属网络,然后在网络节点布置塑料球,建立立体正交金属网络的实际几何尺寸与正视相机、俯拍相机和侧视斜拍相机等所拍摄的塑料球的表观尺寸的定量关系,完成立体视场的预先标定。
建立立体拍摄影像三维坐标映射关系的方法:在立体视场标定基础上,根据立体视场的几何参数来建立正视影像拍摄目标的三维坐标与垂直俯拍影像、影像中同一目标的三维坐标的映射关系(禹明忠, 2002)。
4.4.2.2 新轨迹追踪算法的原理、框架及初步效果
新算法是基于卡尔曼滤波(Kalman, 1960)和匈牙利算法(Kuhn, 1955)原理的一种PTV算法。当获得大量立体拍摄的高速影像后,在风沙图像分割算法基础上(梅凡民等,2018),建立高配准率的新PTV算法尤为关键。前人在最近邻算法的基础上提出了追踪流体示踪粒子的PTV算法如粒子群算法(e.g.Okamoto, et al., 1995; 张扬等, 2010)和神经网络算法(e.g.Ohmi & Sapkota, 2006)等均不适合追踪高浓度风沙颗粒流,这是因为:①最近邻算法仅适用于低浓度风沙颗粒的匹配(Zhang, et al., 2007; Wang, et al.,2008; Yang, et al., 2009; 梅凡民和蒋缠文,2012)而低浓度的粒-床碰撞数据有统计上的局限性; ②粒子群算法基于一定范围内同帧粒子群运动相似性的假定,而速度和方向各异的风沙颗粒流(如床面附近的很小范围内会分别出现入射、溅射、反弹等沙粒,其流场空间变异性很高)很难满足此假定;③神经网络算法因需要大量风沙运动数据集的训练而难以实施。至于最近发展的基于最近邻法则和球形石英颗粒粒径比的PTV算法(O'Brien &Neuman, 2016, 2017)也很难用于实际风沙颗粒的轨迹追踪,这是因为:①沙漠沙形状不规则性使得难以采用粒径比来进行轨迹匹配;②不能解决侧向运动沙粒进入/逸出造成的轨迹配准率较低的问题(18%~35%)。综上,发展新PTV算法来追踪高浓度风沙颗粒轨迹显得十分必要。
鉴于风沙颗粒流流场的空间变异特征与雷达影像中军事目标的机动性特征的相似性,新算法借鉴了雷达影像多目标追踪算法的思路(Reid, 1979; 韩崇昭等, 2010)。在多目标追踪算法中,匈牙利算法是基于二分图理论旨在解决两个数据集合之间的关联问题的方法(Kuhn, 1955),其与风沙颗粒轨迹追踪在本质上是相似,其算法原理是最近邻原则+连续两帧图像目标匹配距离成本最小的约束来实现2帧图像沙粒轨迹的最优匹配,它的优点是计算简洁但缺乏多帧匹配对初始匹配方案的动态纠错功能;多假设算法具有动态纠错功能(Reid, 1979; 韩崇昭等, 2010),其利用多步假设匹配的后验概率来不断地修正初始匹配方案以提高轨迹匹配的精度但算法复杂且计算量大。这里借鉴上述算法的优点和思路提出了新PTV算法框架。新算法包括:①引进卡尔曼滤波算法以减小沙粒位置测量和预测的误差;②建立在同步立体影像对中沙粒的三维坐标映射关系(映射关系是指同一个沙粒如果被2~3相机同时拍摄,形成同一沙粒的影像对,它们之间三维坐标的换算关系)以对二维影像中进入/逸出沙粒轨迹在三维空间上进行匹配,以消除其对二维图像轨迹追踪的干扰;③增加匹配回溯算法功能来动态地优化匈牙利算法上步的匹配方案以实现轨迹的动态优化。传统匈牙利算法会对有限步数内(如5~10步)内未被匹配的沙粒进行删除,而新PTV算法拟通过回溯算法功能实现:a)利用同步立体影像对的三维沙粒坐标的映射关系来判别沙粒是否偏离二维航迹,若偏离则按三维坐标映射关系进行三维轨迹追踪并更新上一步的匹配方案以排除上步二维影像中沙粒匹配的错误; b)若未偏离二维航迹则继续按照匈牙利算法进行匹配;c)若同步影像中既找不到该沙粒也不能在二维影像中被匹配则删除该颗粒以排除干扰;④增加识别入射-反弹和溅射关系的算法模块以建立三维入射-反弹-溅射速度的定量关系。目前的PTV算法均不涉及入射-反弹-溅射关系的识别,在人工识别的基础上,著者提出界定入射-反弹-溅射关系的算法,以揭示三维尺度上的入射-反弹-溅射速度的定量关系。
总之,新PTV算法包括灰度阈值分割+腐蚀膨胀取形心、卡尔曼滤波优化沙粒测量及预测位置、匈牙利算法初始匹配、同步立体影像对三维坐标映射关系查询及三维运动沙粒匹配、回溯算法模块修正匈牙利算法匹配方案、入射与起跳沙粒轨迹筛选、入射-反弹-溅射关系匹配等模块(见图4-7)。
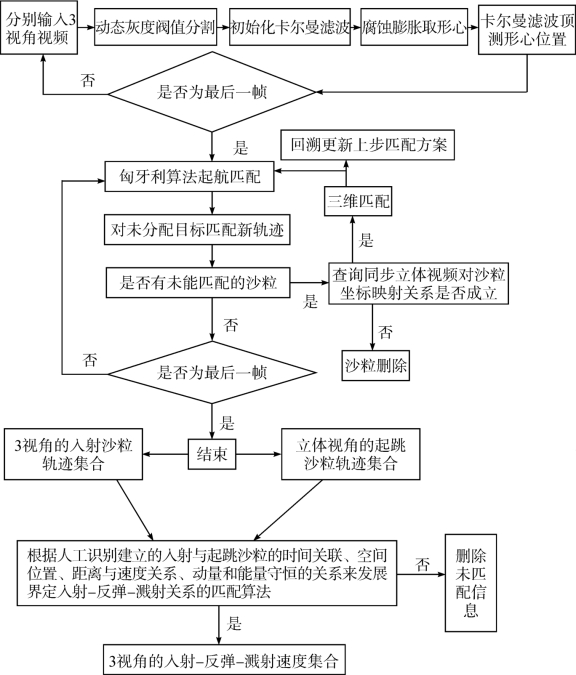
图4-7 新PTV算法的总体框架
和传统的匈牙利算法相比较,新算法增加了同步视频对三维坐标映射关系的查询、三维匹配及对上步匈牙利算法初始方案回溯优化等模块,以解决二维影像中初始错误匹配及侧向运动沙粒匹配错误的问题。
和传统的PTV算法相比较,新算法增加了入射与起跳沙粒轨迹筛选、入射-反弹-溅射关系筛选及匹配模块,可实现从三维视角提取、分析粒-床碰撞信息。
灰度阈值分割算法见参考文献((梅凡民等,2018))。(https://www.daowen.com)
卡尔曼滤波的算法流程包括构建沙粒状态转移矩阵、观测矩阵、系统预测噪声斜方差矩阵、观测噪声协方差矩阵(见图4-8)。通过多步预测和多步测量来不断优化预测和观测的协方差矩阵,从而有效控制沙粒位置预测和测量的误差直到追踪结束。
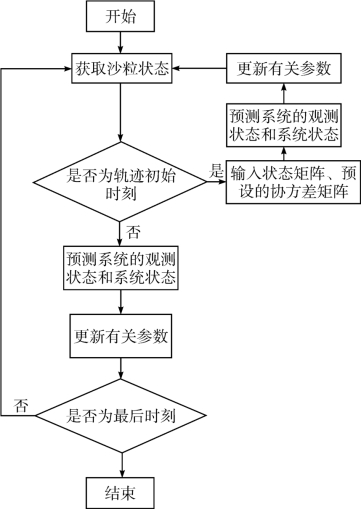
图4-8 风沙图像沙粒位置测量及预测的卡尔曼滤波算法流程(彭青宇, 2020)
卡尔曼滤波的主要功能是保证单个沙粒轨迹匹配的误差最小,而要保证高速影像中多个沙粒匹配误差最小,则需要匈牙利算法的配合。
关于匈牙利算法框架及说明如下(见图4-9):
建立M×N的距离费用矩阵:M为第k帧检测的沙粒数,N是k+1帧检测的沙粒数,计算每一个通过卡尔曼滤波预测获得的结果和每一个检测到的沙粒形心坐标之间的欧拉距离,并将该距离计入距离费用矩阵中对应的位置;
设定距离费用的阈值:该阈值用来判断内是否有目标颗粒匹配的对象,在二维影像中该阈值曾被设置为13.5,具体应根据影像实际特征来确定;
筛选两帧图像匹配的距离费用最小的匹配方案:分别计算第k帧沙粒和第k+1帧沙粒匹配方案的距离费用,并以距离费用最小为最优匹配方案,具体选优方案见下述内容;
筛选两帧图像匹配的距离费用最小的匹配方案:分别计算第k帧沙粒和第k+1帧沙粒匹配方案的距离费用,并以距离费用最小为最优匹配方案,具体选优方案见下述内容;
匹配方案选优流程见图4-9:①对矩阵费用进行变换,将代价矩阵中的每一行减去该行的最小值,每一列减去该列的最小值;②进行试指派,找出独立的0元素,该操作包括距离费用矩阵的每一行,对有且仅有一个0元素所在行对应的零元素画“○”。然后将“○”所在列的其他0元素划去,记作“ø”;从只有一个0元素的列开始(画“ø”的列不计),对该列中的0元素画“○”,然后将“○”所在行的其他0元素划去,记作“ø”;若依然没有画“○”的元素,且同行(列)的0元素至少有两个,比较该行各元素所在列中0元素的数目;选择数目少的画“ø”,然后将同行同列中其他0元素划去;如果矩阵中画“○”的个数等于矩阵的阶数则矩阵中所有画“○”的0元素所对应的行数和列数即为轨迹和沙粒所对应的编号,此时分配已经结束;若画“○”个数与矩阵阶数不相等则重复前面的步骤;③对距离费用矩阵中的0元素用最少的直线进行覆盖,包括对没有“○”的行上画“√”;对画上“√”行中0元素所在的列画上“√”;将画上“√”的列中所有“○”所在的行画上“√”;将距离费用矩阵中未标记“√”的行画上横线,对标记上“√”的列画上竖线,直到矩阵中所有的0元素被覆盖,将覆盖的所有0元素的直线个数记作l,若l小于矩阵阶数则进入第④步;④变换矩阵以添加0元素个数,在没有直线通过的所有元素中找出最小值,没有直线通过的元素减去最小值,直线交点处的元素加上最小值,然后转到第②步。
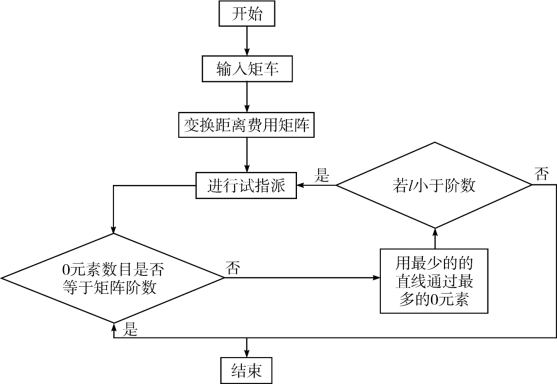
图4-9 风沙图像沙粒轨迹匹配的匈牙利算法选优流程(彭青宇, 2020)
构建界定入射-反弹-溅射关系算法具体包含以下内容:
依靠人工识别的样本来确定界定入射-反弹-溅射关系的方法:时间关系是指溅射和反弹发生在入射之后,具体的时间差可能在10-3 s的数量级(此尺度是著者对二维影像的总结,至于三维影像还应根据粒-床碰撞的工况来确定具体的时间尺度);空间尺度是指反弹和溅射的位置在入射位置的下风向,而溅射位置应在入射或反弹周围或二者之间的位置;反弹的空间可达性是指以拟匹配为反弹颗粒的水平速度来推测其是否在入射与反弹时间差内能通过入射点和反弹点之间的距离,若刚好通过或不通过则满足反弹的条件,否则不满足反弹条件;动能/动量守恒原则是指入射前动能/动量应分别大于反弹和溅射颗粒的动能动量之和。上述关系涉及的具体指标还有待于针对具体情形下人工识别来确定。
构建入射-反弹-溅射的匹配算法的方法:以上述筛选的入射-反弹-溅射定量关系为条件,调用入射沙粒轨迹集合和起跳沙粒轨迹集合的数据,让计算机逐个按照上述定量关系进行界定和配对,直到得到所有图像拍摄视野内入射-反弹-溅射关系及对应沙粒速度数据,为研究三维的粒-床碰撞规律提供分析数据。
图4-10是新轨迹追踪算法应用到二维图像的基本效果,由于二维图像固有的缺陷,该算法在高浓度图像中的处理效果不是很理想。新算法需要借助三维图像的信息以提高沙粒轨迹匹配的精度。
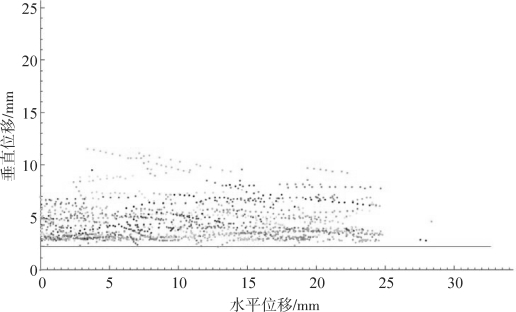
图4-10 基于卡尔曼滤波和匈牙利算法的风沙图像沙粒轨迹匹配效果(彭青宇, 2020)
