1.6.2　积水深度和流速对雨滴分离-雨滴诱导的薄层水输送的模拟

1.6.2　积水深度和流速对雨滴分离-雨滴诱导的薄层水输送的模拟

在雨滴溅蚀-雨滴诱导薄层水输送阶段(RD-RIS),溅蚀输送率可表示为式(1-31)(Kinnell, 1991),其中q′p,d,m′p,d,N′r分别为单位时间单位宽度颗粒输送率、活动带内(active zone)被直径为d的单个雨滴碰撞的粒径为p颗粒的质量、活动带内单位宽度直径为d的雨滴个数:

雨滴溅射的p颗粒进入薄层水中,其水平速度会近似等于uw(薄层水相应高度的平均流速),若它在水中停留时间为t′p,z,则其水平位移x′p,d近似可表示为式(1-32):这里假定溅射上升阶段水平位移为零。

图1-4是单个雨滴溅蚀的颗粒群在薄层水悬浮的示意,图中虚线代表跃移颗粒云的高度,假定单个雨滴撞击的悬浮颗粒云水平分布范围在x′p,d-0.5xcz和x′p,d+0.5xcz之间。

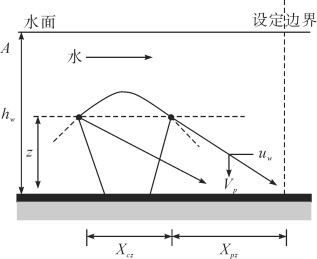
图1-4　雨滴溅射-薄层水抬升的跃移颗粒群输送的示意图

z-跃移颗粒在水中抬升的高度,u-薄层水的流速,hw-薄层水的厚度,Vp-颗粒沉降速度,Xcz-跃移颗粒在水中抬升过程的水平位移,Xpz-跃移颗粒在水中沉降过程中的水平位移,据Kinnell(1991)重绘。

令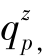d,Fd,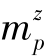,d分别为颗粒被输送到z高度的输送率、直径为d的碰撞雨滴的空间平均频率、单个雨滴溅射并被薄层水输送到z高度的颗粒质量,它们之间关系满足式(1-33):

mp,d=∑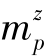,d表示被雨滴溅射-薄层水输送到所有高度的颗粒质量。

Fd与直径为d雨滴的降雨强度Id相关,可表示为式(1-34):

跃移输送的p颗粒群在薄层水中的质量权重平均的停留时间tp为式(1-35):

跃移层内所有高度的p颗粒群输送率qp,d可表示为式(1-36):

式(1-36)中的mp,d和tp不易精确地观测和计算,故重新整理式(1-34)和式(1-36),可得式(1-37):

利用式(1-36)右边易观测的参数来推测mp,dtp的大小。Moss ＆amp; Green(1983)观测表明,当5.1 mm雨滴碰撞0.2 mm的细沙时,且在uw=20 mm·s-1情况下,则mp,dtp随着流深增加而减小;同样地,2.7 mm雨滴碰撞实验也表明,当hw＆lt;3d时,hw对mp,dtp没有很明显的影响(Moss ＆amp; Green, 1983; Kinnell, 1988)。Kinnell(1991)认为前人结果与实验测量误差有关,于是通过沙盘溅蚀实验来重新认识薄层水的uw和hw对mp,dtp和qp,d的影响。

研究结果表明(Kinnell, 1991):①当2.7 mm雨滴以接近终速撞击0.2 mm细沙时,且当降雨控制模块前后移动时,当hw=6 mm时,qp,d随着uw或Id的增加而线性的增加;②当Id=64 mm·h-1, uw=40 mm·s-1,沙粒粒径分别为0.1 mm, 0.2 mm, 0.9 mm时,qp,d随着hw(＆lt;10 mm)增加而线性的减小,可表示为式(1-38),其中Ap,d和Bd分别与沙粒粒径和雨滴特征有关。进一步的数据揭示了当雨滴碰撞前未达到终速时,Ap,d和Bd与雨滴的碰撞速度呈现线性相关。

结合式(1-37)和式(1-38)mp,dtp可表述为式(1-39):其中Ap,d和雨滴和溅蚀颗粒的性质有关,而Bd仅和雨滴特征有关,其适合描述中等、大雨滴撞击松散颗粒表面的情形。

根据定义,跃移颗粒在薄层水中浓度Cp,d可表述为式(1-40):其中qw为薄层水的流量。

由式(1-39)和式(1-40)可得到式(1-41):

前人观测数据表明式(1-39)不仅适用于松散颗粒跃移输送浓度的计算(Moss ＆amp;Green, 1983),也适用于黏结土壤(Kinnell ＆amp; McLachlan, 1989, Kinnell, 1991)。

Cp,d随着Id增加而增加(Walker, et al., 1978; Singer, et al., 1981; Meyer ＆amp; Harmon, 1989),当Id相同时,5%坡度斜坡的Cp,d约为0.5%坡度的3倍(Walker, et al.,1978)。当非均匀雨滴撞击粉壤质土壤时,当坡度从0°增加到30°,Cp,d约从2 g·L-1线性地增加到20 g·L-1。

Kinnell(1991)研究虽然建立了雨滴分离-薄层水跃移输送模型框架,但模式还缺乏估计Ap,d和Bd的普适性公式。鉴于此,Kinnell ＆amp; Wood (1992)开展了3.7 mm雨滴溅蚀-薄层水跃移输送实验。为了让溅蚀沙样在流向获得均等雨滴碰撞机会,特设置雨滴喷头前后匀速移动。设置uw=20 mm·s-1以保证积水无侵蚀能力而仅有输送能力。hw在4.5~11 mm之间。

基于回归分析方法,2.7 mm, 3.7 mm和5.1 mm 均匀雨滴碰撞均匀沙(粒径分别为0.1 mm, 0.2 mm, 0.46 mm, 0.9 mm)及2.7 mm雨滴撞击3类土壤的实验结果表明,式(1-39)中的Ap,d和Bd分布符合式(1-42)和式(1-43):其中Vp是p颗粒在薄层水中的平均沉降速度。

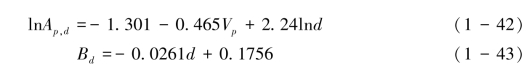
需要说明的是,Ap,d,Bd和d的关系来自3组粒径雨滴溅蚀回归分析结果(2.7 mm,3.7 mm和5.1 mm)。

为了建立非均匀雨滴溅蚀情形下hw与qp,d的定量关系,并分离土壤性质和雨滴特征对qp,d的影响,前人分别引入ks以表征土壤对雨滴溅蚀-薄层水输送的脆弱性、流深函数f(hw,d)以表示流深对qp,d的影响(其数值在0~1之间),则式(1-38)可表示为式(1-44):

分析当uw=20 mm·s-1, Id=64 mm·h-1时,2.7 mm, 3.7 mm和5.1 mm雨滴撞击0.9 mm沙的qp,d与hw的关系,Kinnell ＆amp; Wood (1992) 发现f(hw,d)可分别表示为式(1-45)和式(1-46):

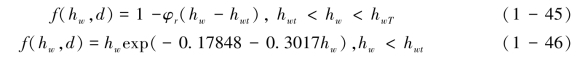
其中φr=0.3119-0.0507d, hwt是指在qp,d与hw的关系图中,qp,d随hw变化的转折点对应的水深,水深小于此数值则qp,d随hw以式(1-46)所示的变化,大于此数值以式(1-45)所示的变化。在上述实验中,hwt=4.8 mm; hwT意味着水深超过某个阈值时,qp,d不再随水深变化,雨滴溅蚀的影响可忽略。

与中、大雨滴碰撞下流深对qp,d的影响不同,小雨滴碰撞情形下f(hw,d)可表示为式(1-47)~式(1-49):

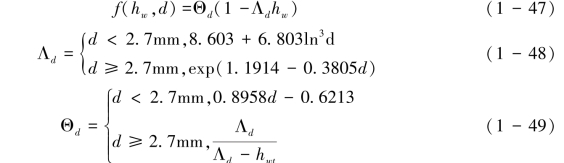
考虑到天然降雨谱的多粒径的特征,则相应的溅蚀-薄层水输送模式和流深函数分别表示为式(1-50)和式(1-51):其中I表示降雨时间中所有雨滴的降雨强度。

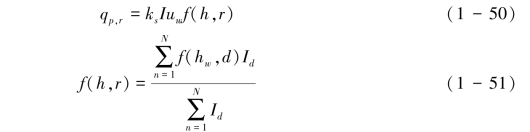
结合Hairsine(1988)数据,Kinnell ＆amp; Wood(1992)发现式(1-51)能够再现自然降雨下流深函数随流深的变化趋势,且在降雨强度和薄层流速恒定的情况下,式(1-50)所预测的qp,r和f(h,r)呈现线性关系,其拟合的直线斜率反映不同土壤的ks。

鉴于上述的流深函数是从d≤5.1 mm的雨滴碰撞实验上发展而来,可能不适合用来预测其他粒径雨滴的溅蚀。为了进一步理解流深对雨滴碰撞薄层水跃移输送的理解,Kinnell(1993a)更新了上述流深函数。根据定义,qp,d=qwCp,d,其中qw=hwuw为薄层水的流量,Cp,d为颗粒浓度,据此式(1-40)可变形为式(1-52):

令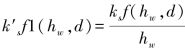,f1(hw,d)在0~1之间,k′s≠ks,则式(1-44)可变形为式(1-53):

其中k′s表征了土壤对雨滴碰撞流的敏感程度,其大小只与土壤性质有关。以式(1-47)为框架,重新对0.1 mm, 0.2 mm, 0.9 mm雨滴碰撞实验数据进行回归分析(Kinnell＆amp; Wood,1992),前人发现如下关系如式(1-54)~式(1-56):

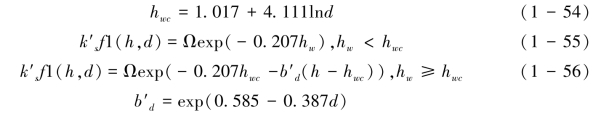
令Ω=k′s以简化上述公式,得到新的流深函数式(1-57):

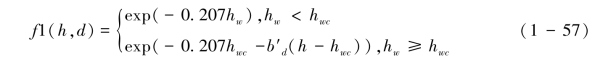
和以前的研究相比较(Kinnell ＆amp; Wood,1992),新研究定量地确定了hwc的数值(Kinnell, 1993a),并以此确定了雨滴撞击对薄层流水中跃移颗粒输送影响程度的差异:当hw＆lt;hwc时,雨滴大小和动能对溅蚀输送和跃移颗粒浓度影响较小,这时薄层水仅仅约束了溅蚀颗粒跳跃高度;当水深超过此阈值,薄层水阻滞和对雨滴动能消耗更大,因而雨滴大小和动能会影响颗粒输送强度和浓度。

相应地,qp,d可表示为式(1-58):这里F2(hw,d)=hwF1(hw,d)

需要说明的是,式(1-57)是具有一定普适性的统计模型。尽管如此,当存在与预测情形相似的观测数据时,可对相似观测数据进行统计分析。在Kinnell之后的研究中(e.g.Kinnell, 2009, 2013),d=2.7 mm情形提出的流深函数则更适用于对应情况,其具体形式这里不再赘述。